【作业内容】:用Matlab编程求方程,分别求
f ( x ) = x 5 − 12.5 x 4 + 57.5 x 3 − 118.75 x 2 + 105.5625 x − 29.53125 = 0 f(x) = x^{5}-12.5x^4 +57.5x^3 -118.75x^2 + 105.5625x -29.53125 = 0 f(x)=x5−12.5x4+57.5x3−118.75x2+105.5625x−29.53125=0
在区间 ( 0 , 1 ) , ( 1 , 2 ) , ( 2 , 3 ) , ( 3 , 4 ) (0,1),(1, 2),(2, 3),(3, 4) (0,1),(1,2),(2,3),(3,4)和 ( 4 , 5 ) (4,5) (4,5)中的根,初值分别取为 0.1 , 1.1 , 2.1 , 3.1 0.1,1.1,2.1,3.1 0.1,1.1,2.1,3.1和 4.1 4.1 4.1。
【作业要求】:
-
你自己设计一种不动点迭代法,要使迭代序列收敛,使得 ∣ x k − x k − 1 ∣ < 1 0 − 8 |x_k - x_{k-1}|<10^{-8} ∣xk−xk−1∣<10−8 为止. 输出迭代初值及各次迭代初值和迭代次数 k k k
-
用牛顿迭代法,计算到 ∣ x k − x k − 1 ∣ < 1 0 − 8 |x_k - x_{k-1}|<10^{-8} ∣xk−xk−1∣<10−8为止.输出迭代初值及各次迭代值和迭代次数 k k k
-
比较上述两种方法的优劣.
你自己设计一种不动点迭代法,要使迭代序列收敛,使得 ∣ x k − x k − 1 ∣ < 1 0 − 8 |x_k - x_{k-1}|<10^{-8} ∣xk−xk−1∣<10−8 为止. 输出迭代初值及各次迭代初值和迭代次数 k k k
- 首先构造迭代方程 φ ( x ) varphi(x) φ(x)
φ 1 ( x ) = ( ( − 12.5 ∗ x 4 + 57.5 ∗ x 3 − 118.75 ∗ x 2 + 105.5625 ∗ x − 29.53125 ) / ( − 1 ) ) 1 5 φ 2 ( x ) = ( ( x 5 + 57.5 ∗ x 3 − 118.75 ∗ x 2 + 105.5625 ∗ x − 29.53125 ) / 12.5 ) 1 4 φ 3 ( x ) = ( ( x 5 − 12.5 ∗ x 4 − 118.75 ∗ x 2 + 105.5625 ∗ x − 29.53125 ) / ( − 57.5 ) ) 1 3 φ 4 ( x ) = ( ( x 5 − 12.5 ∗ x 4 + 57.5 ∗ x 3 + 105.5625 ∗ x − 29.53125 ) / 118.75 ) 1 2 φ 5 ( x ) = ( ( x 5 − 12.5 ∗ x 4 + 57.5 ∗ x 3 − 118.75 ∗ x 2 − 29.53125 ) / ( − 105.5625 ) ) begin{aligned} varphi_1(x) &=((-12.5*x^4+57.5*x^3-118.75*x^2+105.5625*x-29.53125)/(-1))^{frac{1}{5}}\ varphi_2(x) &=((x^5+57.5*x^3-118.75*x^2+105.5625*x-29.53125)/12.5)^{frac{1}{4}}\ varphi_3(x) &=((x^5-12.5*x^4-118.75*x^2+105.5625*x-29.53125)/(-57.5))^{frac{1}{3}}\ varphi_4(x) &=((x^5-12.5*x^4+57.5*x^3+105.5625*x-29.53125)/118.75)^{frac{1}{2}}\ varphi_5(x) &=((x^5-12.5*x^4+57.5*x^3-118.75*x^2-29.53125)/(-105.5625))\ end{aligned} φ1(x)φ2(x)φ3(x)φ4(x)φ5(x)=((−12.5∗x4+57.5∗x3−118.75∗x2+105.5625∗x−29.53125)/(−1))51=((x5+57.5∗x3−118.75∗x2+105.5625∗x−29.53125)/12.5)41=((x5−12.5∗x4−118.75∗x2+105.5625∗x−29.53125)/(−57.5))31=((x5−12.5∗x4+57.5∗x3+105.5625∗x−29.53125)/118.75)21=((x5−12.5∗x4+57.5∗x3−118.75∗x2−29.53125)/(−105.5625))
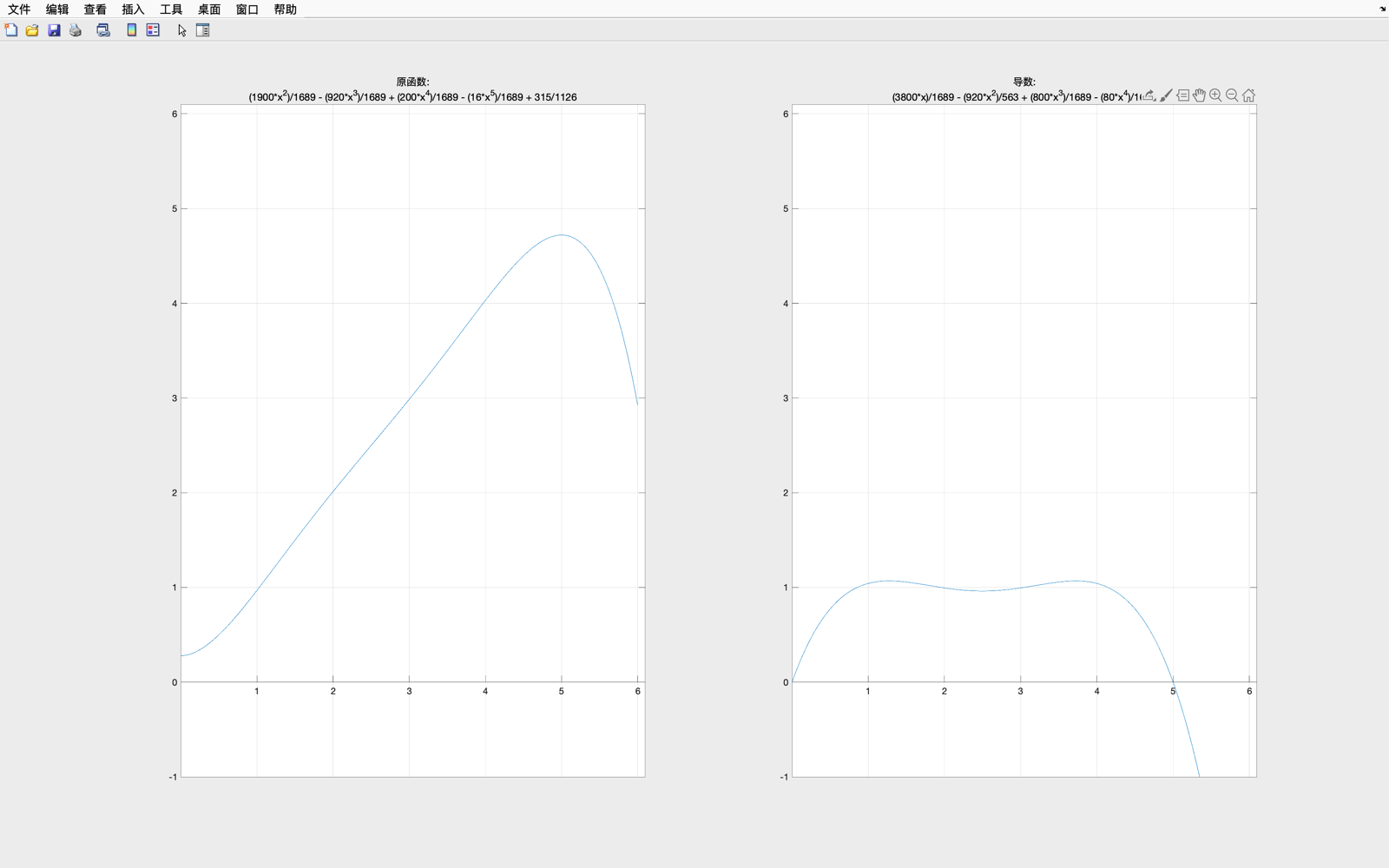
绘制 φ ( x ) varphi(x) φ(x) 与 φ ′ ( x ) varphi'(x) φ′(x)的图像,找到合适的迭代区间
matlab自定义脚本如下:
clear;
clc;
syms x;
% 依次绘制图像
f(x)=((-12.5*x^4+57.5*x^3-118.75*x^2+105.5625*x-29.53125)/(-1))^(1/5);
Plot_Test(f);
% g(x)=((x^5+57.5*x^3-118.75*x^2+105.5625*x-29.53125)/12.5)^(1/4);
% Plot_Test(g);
%
% h(x)=((x^5-12.5*x^4-118.75*x^2+105.5625*x-29.53125)/(-57.5))^(1/3);
% Plot_Test(h);
%
% p(x)=((x^5-12.5*x^4+57.5*x^3+105.5625*x-29.53125)/118.75)^(1/2);
% Plot_Test(p);
%
% q(x)=((x^5-12.5*x^4+57.5*x^3-118.75*x^2-29.53125)/(-105.5625));
% Plot_Test(q);
具体绘制代码:
function [] = Plot_Test(f)
syms x;
% 求出导函数
df(x) = diff(f(x));
x0 = 0:0.001:6;
y0 = f(x0);
x1 = 0:0.001:6;
y1 = df(x1);
% 绘制原函数以及导函数图像
subplot(1,2,1);
plot(x0,y0),grid on;
title(['原函数:',string(f(x))])
xlim([0 6.1]);
ylim([-1 6.1]);
% 设置坐标轴
ax = gca;
ax.XAxisLocation = 'origin';
ax.YAxisLocation = 'origin';
subplot(1,2,2);
plot(x1,y1),grid on;
title(['导数:',string(df(x))])
% 设置坐标轴
ax = gca;
ax.XAxisLocation = 'origin';
ax.YAxisLocation = 'origin';
xlim([0 6.1]);
ylim([-1 6.1]);
end
经验证, φ 1 ( x ) varphi_1(x) φ1(x) 与 φ 1 ′ ( x ) varphi_1'(x) φ1′(x)在 [ 4 , 5 ] [4,5] [4,5]之间可进行迭代
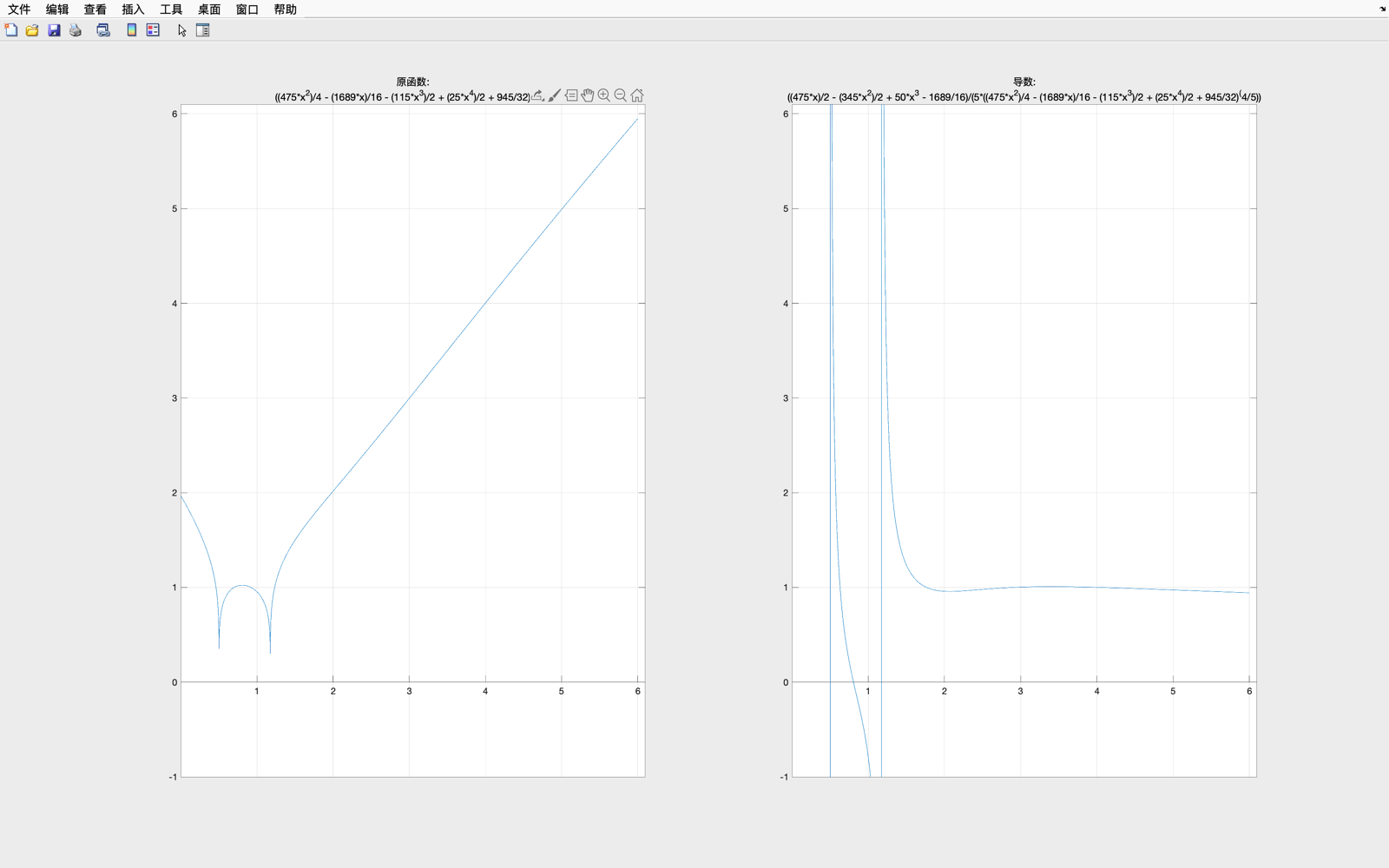
经验证, φ 2 ( x ) varphi_2(x) φ2(x) 与 φ 2 ′ ( x ) varphi_2'(x) φ2′(x)在 [ 3 , 4 ] [3,4] [3,4]之间可进行迭代
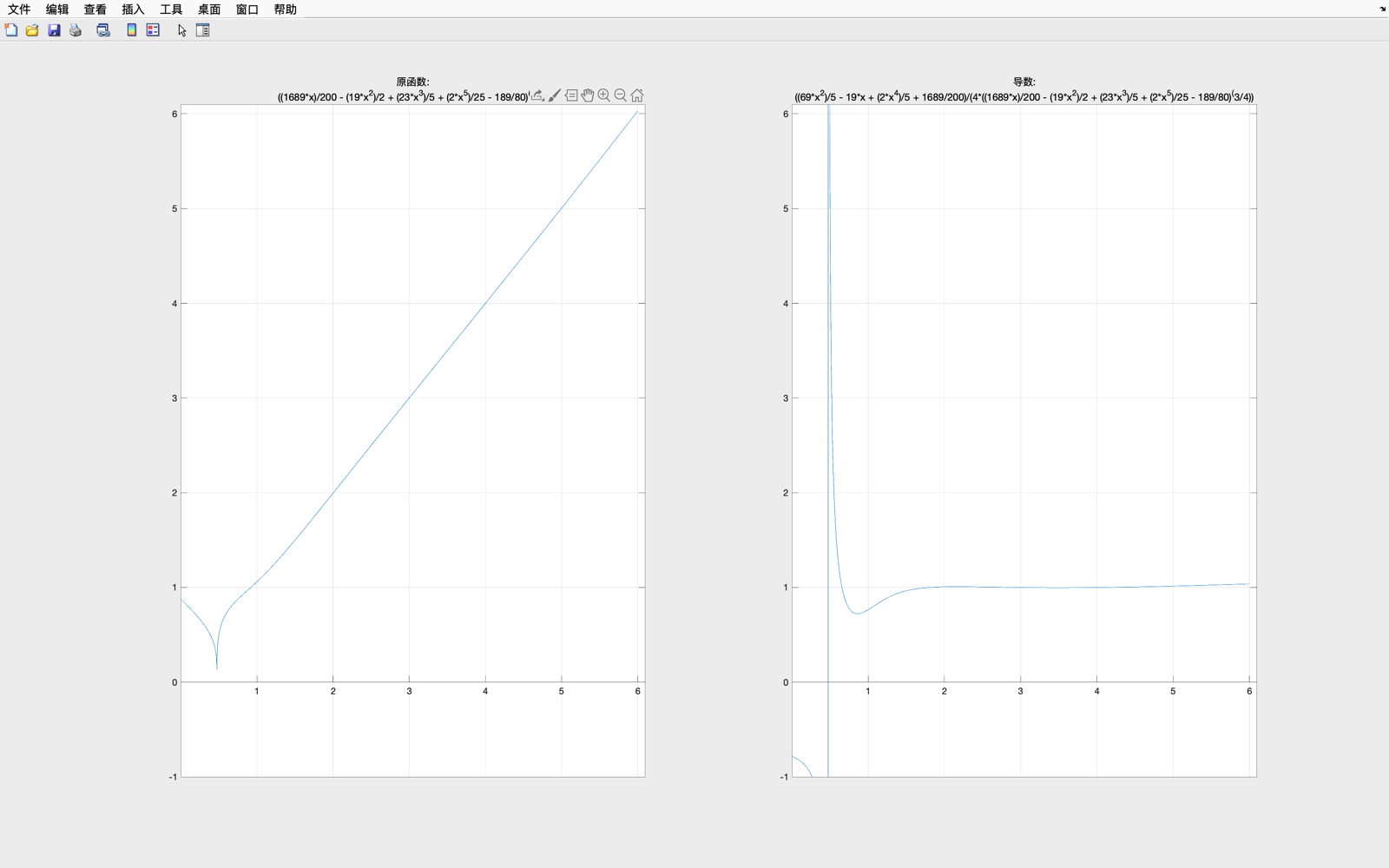
经验证, φ 3 ( x ) varphi_3(x) φ3(x) 与 φ 3 ′ ( x ) varphi_3'(x) φ3′(x)在 [ 2 , 3 ] [2,3] [2,3]之间可进行迭代
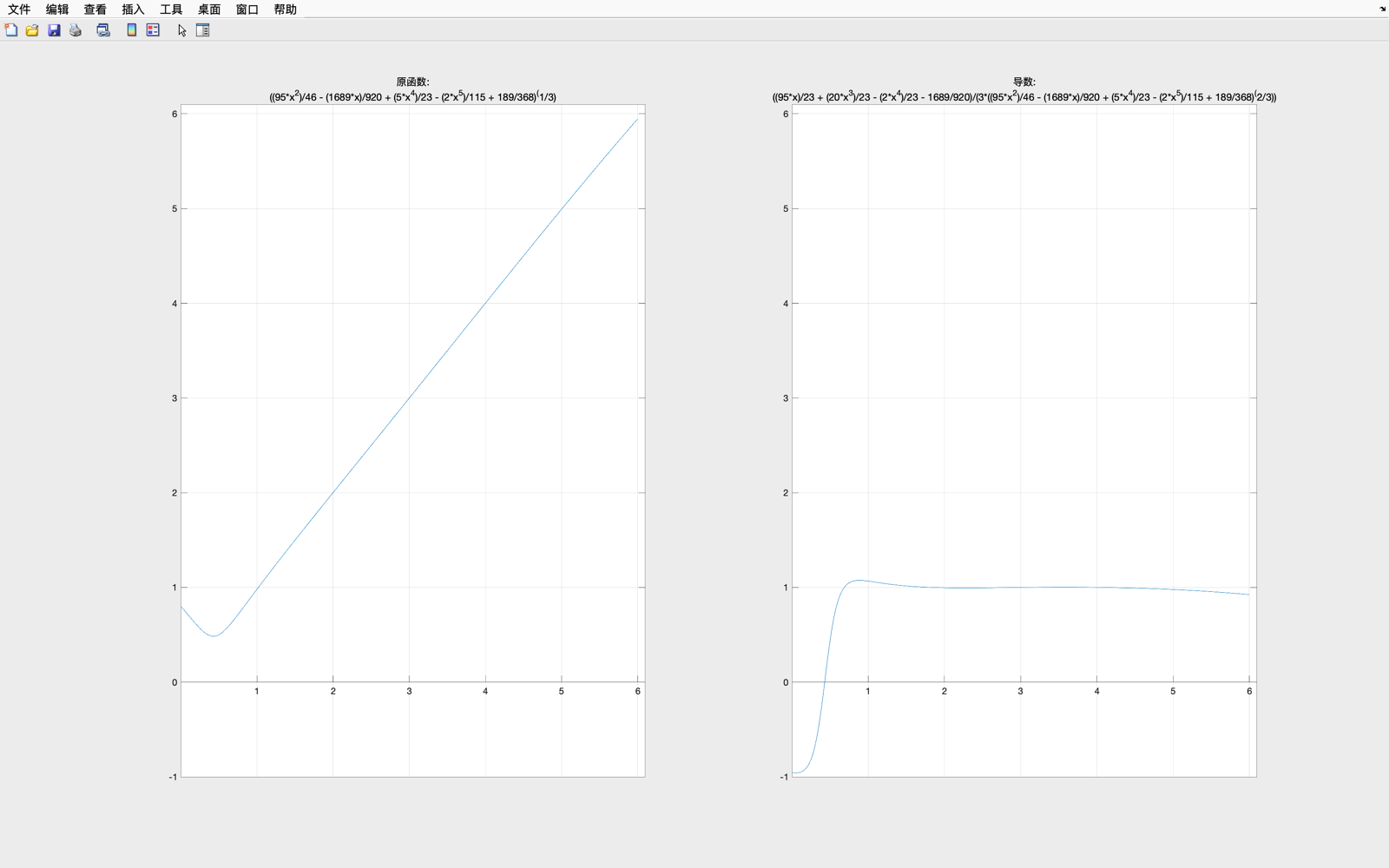
经验证, φ 4 ( x ) varphi_4(x) φ4(x) 与 φ 4 ′ ( x ) varphi_4'(x) φ4′(x)在 [ 1 , 2 ] [1,2] [1,2]之间可进行迭代
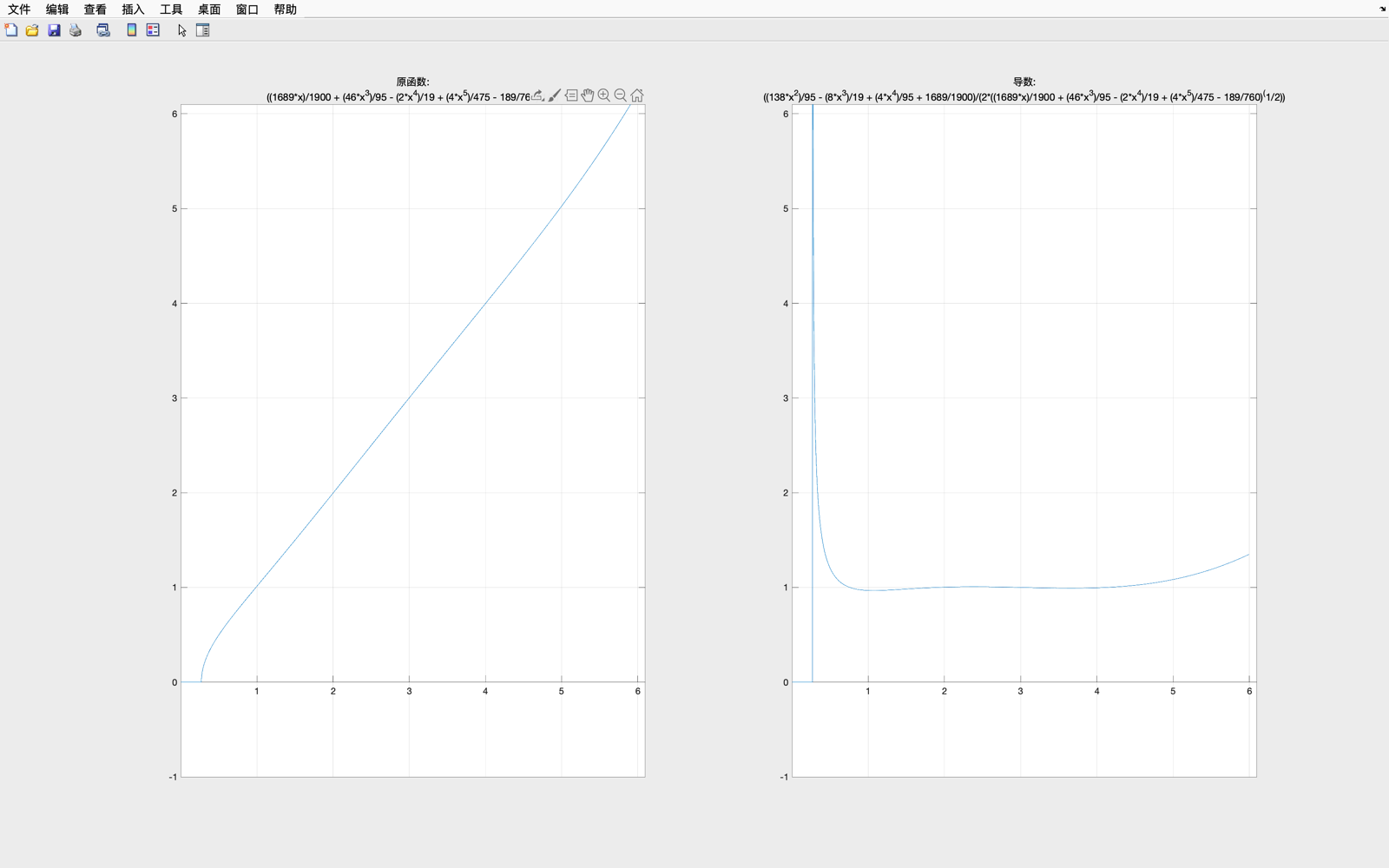
经验证, φ 5 ( x ) varphi_5(x) φ5(x) 与 φ 5 ′ ( x ) varphi_5'(x) φ5′(x)在 [ 0 , 1 ] [0,1] [0,1]之间可进行迭代
不动点迭代法函数matlab代码如下:
% Nonlinear_Iteration.m
function Nonlinear_Iteration(f,start)
format long;
disp('不动点迭代方程为:')
disp(f)
st = start;
disp(['迭代初值为:',num2str(start)])
x=feval(f,st);
Eps=1E-8;
i=1;
while 1
x0=x;
i=i+1;
x=feval(f,x);
if ~isreal(x) % 不是实数不进行迭代
break;
end
if x>1E10 % 若大于给定值,则发散,不进行迭代
break;
end
if abs(x-x0)<Eps
break;
end
end
% 输出迭代次数以及解
disp(['迭代次数为:',num2str(i)])
disp('迭代产生的解为:')
disp(x)
format short;
end
% 由不同迭代方程进行不动点迭代
f=inline('((-12.5*x^4+57.5*x^3-118.75*x^2+105.5625*x-29.53125)/(-1))^(1/5)');
g=inline('((x^5+57.5*x^3-118.75*x^2+105.5625*x-29.53125)/12.5)^(1/4)');
h=inline('((x^5-12.5*x^4-118.75*x^2+105.5625*x-29.53125)/(-57.5))^(1/3)');
p=inline('((x^5-12.5*x^4+57.5*x^3+105.5625*x-29.53125)/118.75)^(1/2)');
q=inline('((x^5-12.5*x^4+57.5*x^3-118.75*x^2-29.53125)/(-105.5625))');
Nonlinear_Iteration(f,4.1);
Nonlinear_Iteration(g,3.1);
Nonlinear_Iteration(h,2.1);
Nonlinear_Iteration(p,1.1);
Nonlinear_Iteration(q,0.1);
用牛顿迭代法,计算到 ∣ x k − x k − 1 ∣ < 1 0 − 8 |x_k - x_{k-1}|<10^{-8} ∣xk−xk−1∣<10−8为止.输出迭代初值及各次迭代值和迭代次数 k k k
matlab代码如下:
format long;
f=inline('x-(x^5-12.5*x^4+57.5*x^3-118.75*x^2+105.5625*x-29.53125)/(5*x^4-50*x^3+172.5*x^2-237.5*x+105.5625)');
for j=0.2:1:4.2
disp(['迭代初值为:',num2str(j)])
x=feval(f,j);
Eps=1E-8; % 设置精度
i=1;
while 1
x0=x;
i=i+1;
x=feval(f,x); % 进行迭代
if ~isreal(x) % 不是实数不进行迭代
break;
end
if x>1E10 % 若大于给定值,则发散,不进行迭代
break;
end
if abs(x-x0)<Eps % 达到设定精度后退出
break;
end
end
% 输出迭代次数以及解
disp(['迭代次数为:',num2str(i)])
disp(['迭代产生的解为:',num2str(x)])
format short;
end
比较上述两种方法的优劣.
使用牛顿迭代法的迭代次数明显少于(1)中的不动点迭代法,且无需考虑
牛顿迭代法的初值选取对迭代的收敛速度与收敛目标景响较大;
要求f(x)有 2 阶连续的导数,条件比较强。
最后
以上就是受伤摩托最近收集整理的关于实验三 解非线性方程的迭代法Matlab实现的全部内容,更多相关实验三内容请搜索靠谱客的其他文章。








发表评论 取消回复