动态规划：值函数迭代例子

• 最优方程：
  V ( h ) = min ⁡ { R + α [ P 1 C + V ( 0 ) ] , α [ h P 2 C + ( 1 − h ) γ P 2 C + ( 1 − h ) ( 1 − γ ) P 1 C + V ( h + ( 1 − h ) γ ) ] } V(h)=min left{R+alphaleft[P_{1} C+V(0)right]right., left.alphaleft[h P_{2} C+(1-h) gamma P_{2} C+(1-h)(1-gamma) P_{1} C+V(h+(1-h) gamma)right]right} V(h)=min{R+α[P1​C+V(0)],α[hP2​C+(1−h)γP2​C+(1−h)(1−γ)P1​C+V(h+(1−h)γ)]}
  其中，$P_2>P_1$。

• 值迭代：
  V n ( h ) = min ⁡ { R + α [ P 1 C + V n − 1 ( 0 ) ] , α [ h P 2 C + ( 1 − h ) γ P 2 C + ( 1 − h ) ( 1 − γ ) P 1 C + V n − 1 ( h + ( 1 − h ) γ ) ] } V_{n}(h)=min left{R+alphaleft[P_{1} C+V_{n-1}(0)right]right., left.alphaleft[h P_{2} C+(1-h) gamma P_{2} C+(1-h)(1-gamma) P_{1} C+V_{n-1}(h+(1-h) gamma)right]right} Vn​(h)=min{R+α[P1​C+Vn−1​(0)],α[hP2​C+(1−h)γP2​C+(1−h)(1−γ)P1​C+Vn−1​(h+(1−h)γ)]}
  其中，$V_0(h)\equiv 0$。

• 离散化：
  因为$h\in [0,1]$，所以我们要对$h$进行离散化。设 h ∈ H = { 0.01 k ∣ 0 ≤ k ≤ 100 , k ∈ N } hin H={0.01k|0le k le100, kin N} h∈H={0.01k∣0≤k≤100,k∈N}。
  又因为$h+(1-h)\gamma$可能不属于$H$，所以我们要将其近似为$H$中最近的元素：$\text{round}(100(h+(1-h)\gamma ))/100$。

• MATLAB实现：

R = 100;
a = 0.9;
P1 = 0.1;
P2 = 0.5;
C = 20;
gamma = 0.5;

V = zeros(101, 100); % V(i,j)表示第j次迭代中第i个状态所对应的值函数的值
for j = 2:100
    for i = 1:101
        h = (i - 1) / 100;
        V(i, j) = min(R + a * (P1 * C + V(1, j-1)), ...
           a * (h * P2 * C + (1 - h ) * gamma * P2 * C ...
           + (1 - h) * (1 - gamma) * P1 * C)...
           + V(round((h + (1 - h) * gamma) * 100) + 1, j - 1));
    end
end

p = 0:0.01:1;
plot(p, V(:,100))

• 实验结果：
  

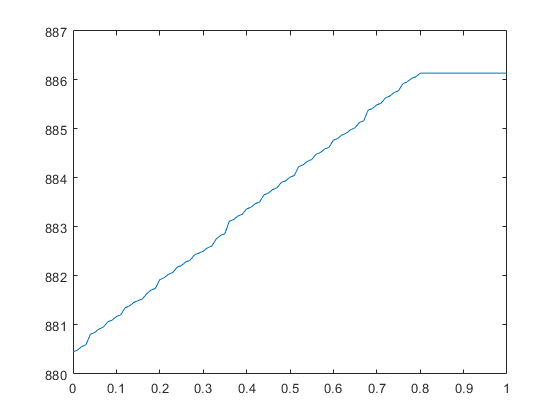
最后

以上就是欣喜大象为你收集整理的动态规划：值函数迭代例子的全部内容，希望文章能够帮你解决动态规划：值函数迭代例子所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。