ga设置迭代次数_仅仅两行迭代就能作出这么惊艳的图像

本人在MATLAB对某个课题进行研究的过程中，意外发现了用最简单的弧线和直线作螺旋图像的方法。

本文的主要想讲以下内容：

一、是记录和展示这个有趣的现象，用数据可视化展现数学之美

二、是以这个现象为例展现一下对某种事物或者现象的探究过程

——从了解表象在到研究其本质，总结归纳有意义的方法和结论

三、顺带练习练习matlab

PS：先给大家看图，毕竟大多数人都是看个新鲜，当然原理的讲解也是有的，我放在最后面了。

一、效果图：

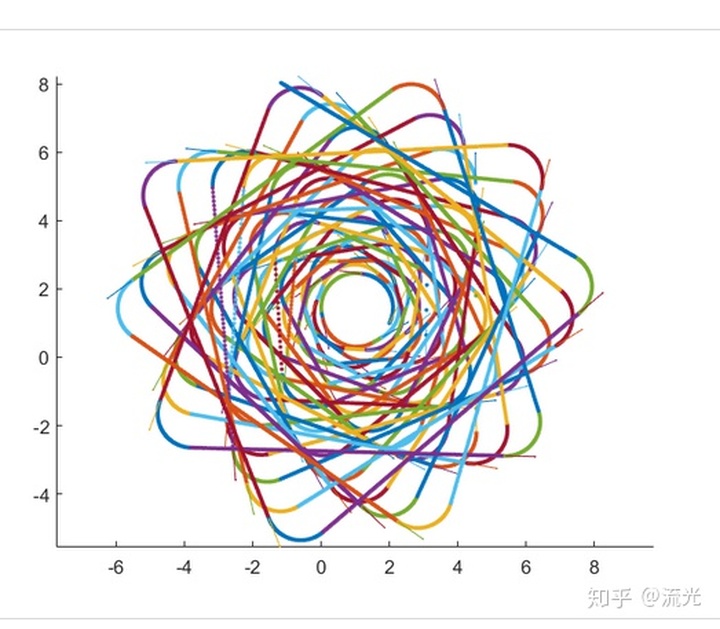
是不是有种抽象画风的感觉

别急还有更酷的

玫瑰花：

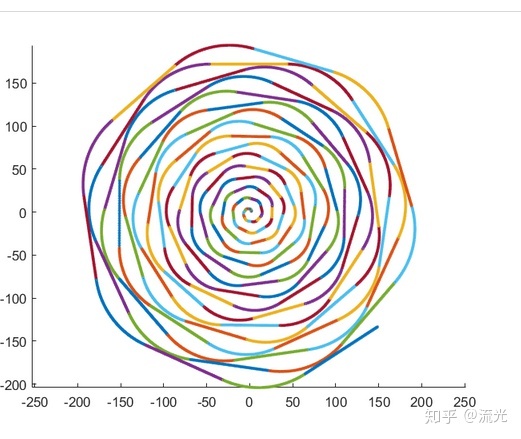
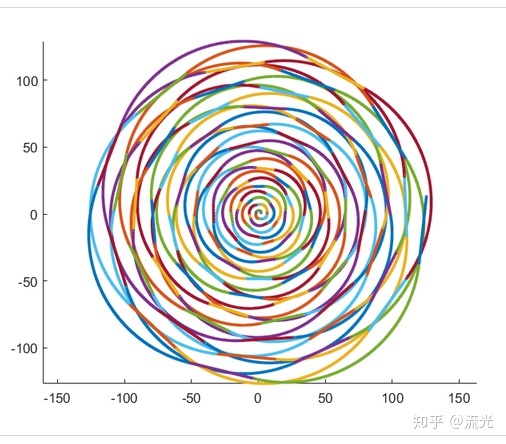
大风车

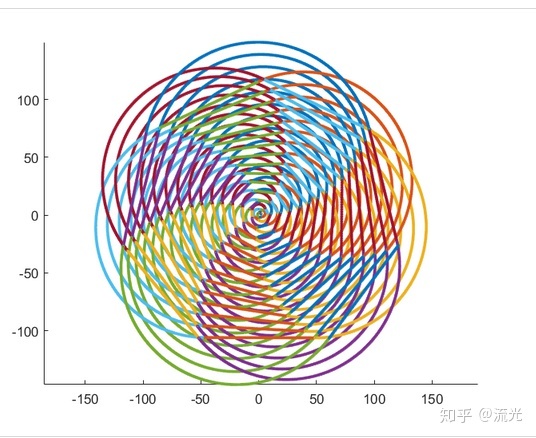
有点像360极速浏览器，啊哈哈

五彩棒

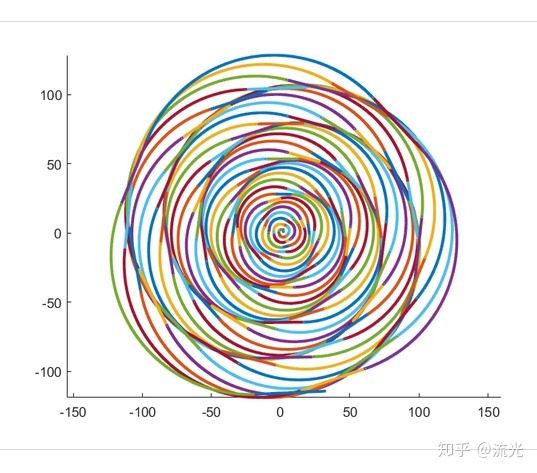
可以拿来当个APP图标，还凑合

像圆形，三角形，正方形，五边形，六边形的迭代图像都可以很简单地作出

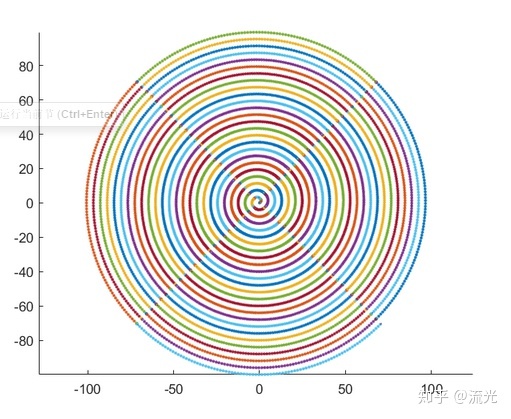
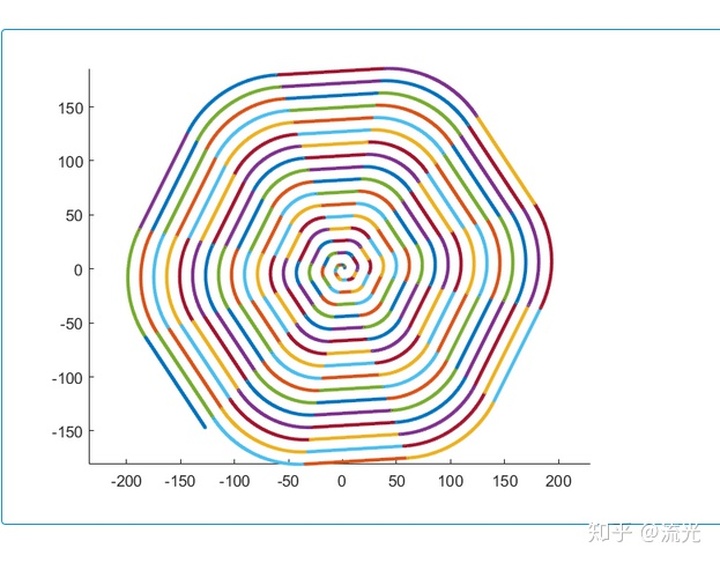
我个人经过计算得到了五角星的图案，注意是“五角星”

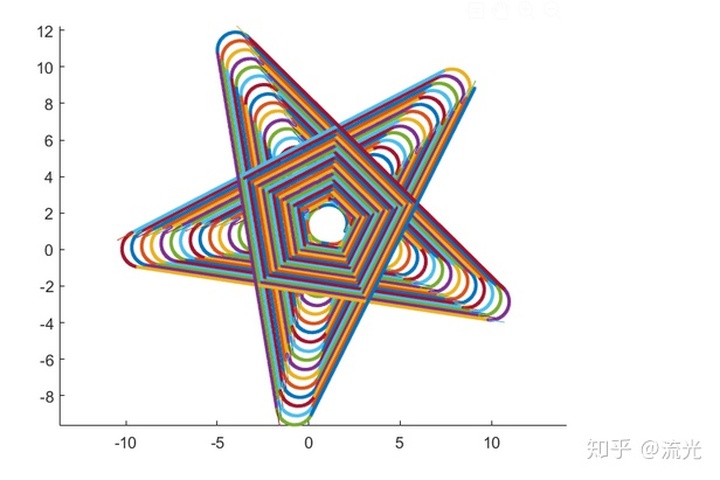
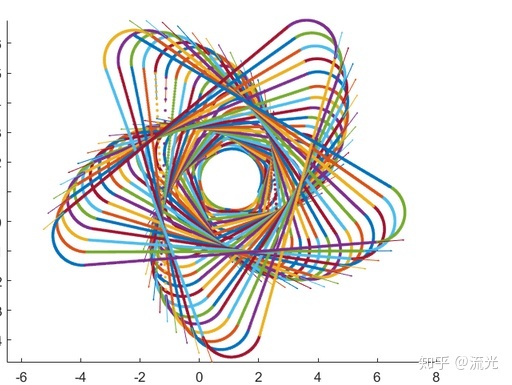
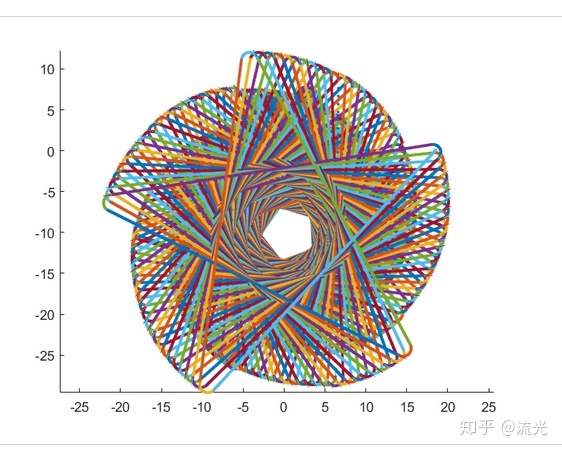
二、原理讲解：

以上所有图案都是在下面这个螺旋线的基础上，复合构造函数作出的

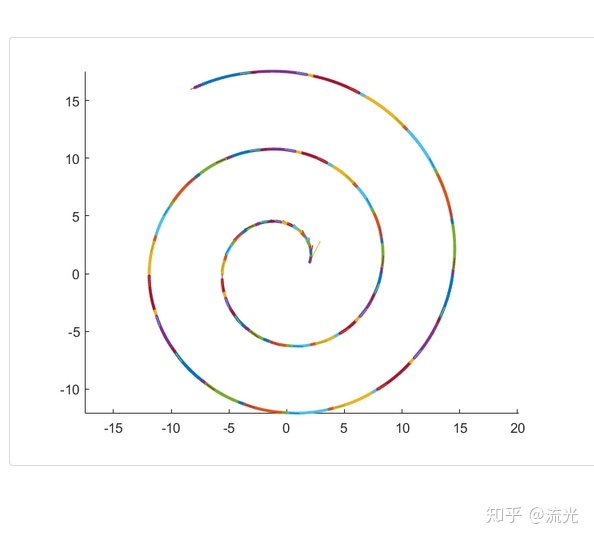
下面是MATLAB的代码，关键只有第3行和第4行

xv=[2,1,1,2];%初始化设置起点坐标以及方向向量
for i=1:1:50%设置循环次数 [xv,mx,my]=draw_sarc(xv,0.3*i,0.3);%画弧 [xv,mx,my]=draw_sline(xv,0.5);%画直线
end

非常好理解，就是这俩两个语句执行五十次

我们直接看循环里的语句

1.[xv,mx,my]=draw_sarc(xv,R,A);画弧

R是半径，A是圆形角，xv 是起始点的坐标以及向量

2.[xv,mx,my]=draw_sline(xv,L);画线

L是直线的长度，xv是起始点的坐标以及方向

意思就是我们先画一条弧线，然后再在上条弧线的末端接着画一条直线，然后再接着画弧，再画直线，依次递推

比如设置圆心角90°，弧的半径为1，直线的长度为1，执行两次如图

圆弧——直线——圆弧——直线——......

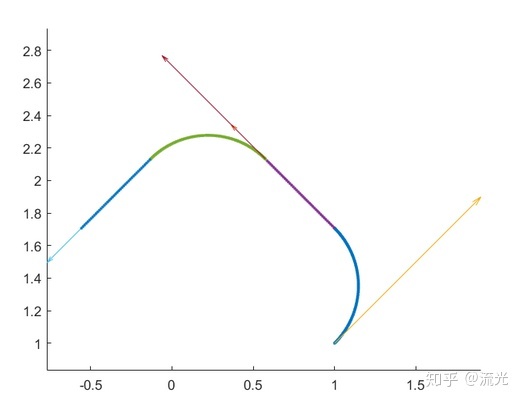
OK完成两次

之后循环上百次就可以了

创造绚丽图案的关键在于

不同的图案是由于R，A，L三个参数，以及迭代次数决定的

R，A，L可以是固定的常数，也可以是迭代次数的函数R（i）、A(i)、L（i）

自由调整参数，或者构造函数创造出更多的参数，就可以产生无穷多种的图案

-----------------------------------------------------------------------------------------------------------------------------------------分界线------------------------------------------------------------------------------------------------------------------------------------------

今天更新给大家简单介绍下，这三个R（i）、A(i)、L（i）的几种构造方法，直观易懂

一、首先是最简单的常数型（让这个三个函数为定值）

（一万能脑残尝试法

常数有啥技巧嗯？没有技巧！随便三个数扔进去看

1.开始尝试

R（i）=r（弧的半径） L（i）=l（延长直线的长度） A（i）=a（弧的角度）

我设一个emmm。。。。——233

（1）R（i）=2 L（i）=3 A（i）=3

画一下看看效果，一看这是嘛玩意儿，233果然不靠谱

换一个试试 666，这么6应该可以吧

（2）R（i）=6.66 L（i）=6.66 A（i）=6.66

哎呦喂不错呦，有点看头

再来试试把R调大到18，为了让圆更大

（3）R（i）=6.66 L（i）=18 A（i）=6.66

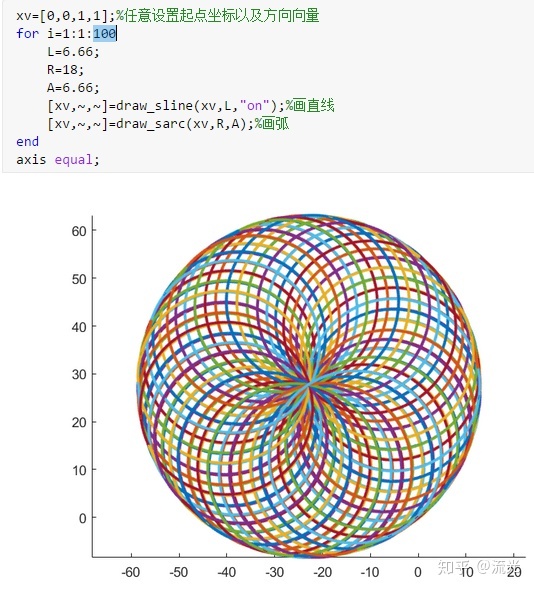
2.结论：

直接挑选常数进行作图，简单易操作，虽然尝试次数够多总会出现满意的图像

但是大多情况下往往是杂乱不堪，没有意义的图案，这种方法盲目、效率低下，我们需要总结归纳和分析

（二）模型构建法

1.计算模型

（1）前面的原理讲解介绍了所有的图像都由

弧线——直线——弧线——直线——……

不断首尾相连得到。

通过计算我们可以作出任意的正多边形（三角形、正方形、五边形、六边形、）

R（i）=10 L（i）=5 A（i）=5π/3

我们可以看到A=5π/3，这样作出来就是一个六芒星

A=2π/5就是一个五边形

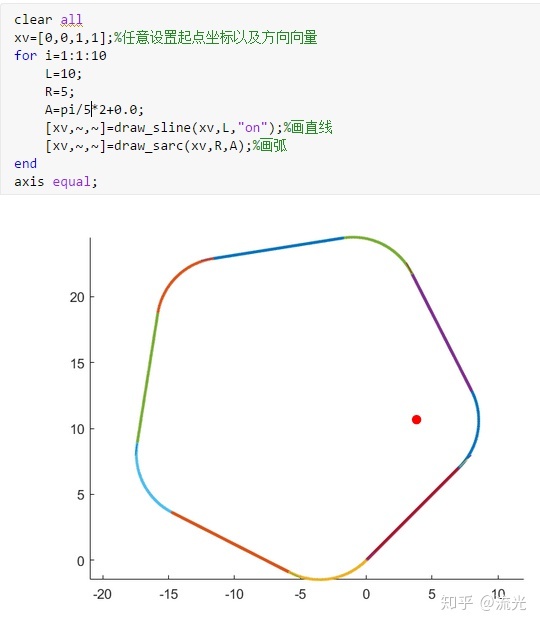
（2）选择，A=N*（30°、45°、60°）N为正整数、任意构造一个正多边形进入下一步

R（i）=10 L（i）=5 A（i）=5π/3

2.模型旋转

（1）在A上加一个△A微小量，△A约为0.02-0.07左右

比如以前面的六芒星为例

R（i）=10 L（i）=5 A（i）=5π/3+0.05

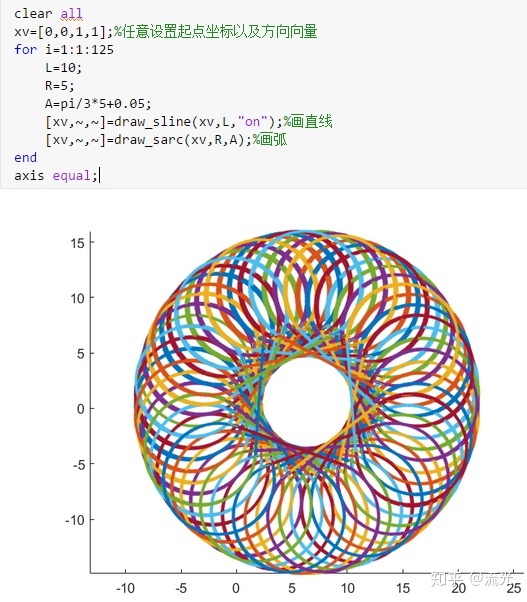
（2）得到由原来模型不断旋转叠加所作出的图形，每次旋转的角度由△A影响，越大旋转速度越快，为了让做出来的图像更细腻更有有视觉冲击感，建议间隔越小越好，但是这样需要增加迭代的次数至少为N（min）

N（min）=2π/△A

否则图像不完整

当△A=0.02时，N=314（次）

当△A=0.05时，N=125（次），所以上例迭代125次

3.结论

比较完美地解决了常数型构造的作图方法和原理，直接计算得到目标图案，先找到正多边形的模型，再通过增加△A得到旋转图像，但是这样得到的图像都是旋转叠加的图像，无论原有的模型是什么形状，最后得到的图像都大致相同轮廓为圆形、里面密铺弧线、比较单一没什么看点，所以我们需要更复杂的构造函数

二、LR一次函数型（LR的值与i迭代次数一次线性关联）

我的这个作图方法理论上可以作任意的一笔画图像，只要函数构造对了.......

(下面的例子我就先放这了，等着有空回来更新整理，溜了溜了~)

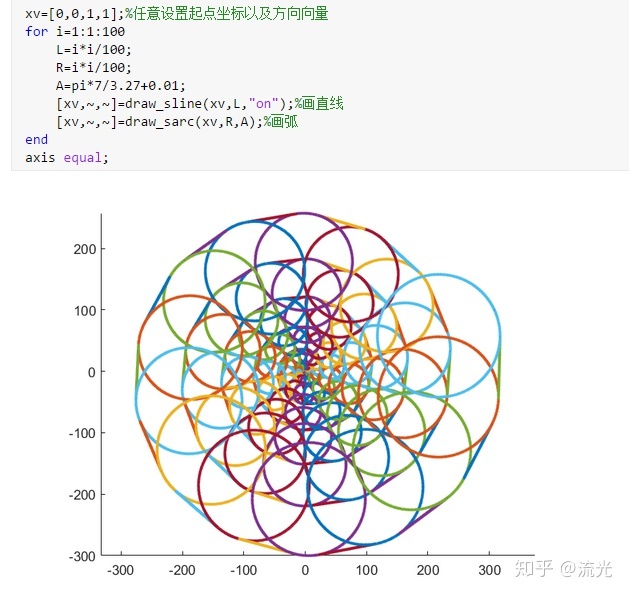
xv=[0,0,1,1];%任意设置起点坐标以及方向向量
for i=1:1:100
    L=i;
    R=i*i/50;
    A=pi*4/3+0.02;
    [xv,~,~]=draw_sline(xv,L,"on");%画直线
    [xv,~,~]=draw_sarc(xv,R,A);%画弧
end
axis equal;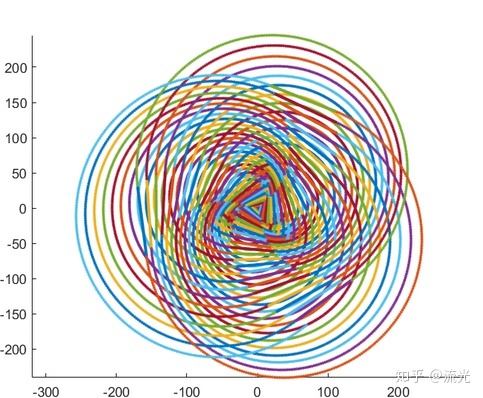

xv=[0,0,1,1];%任意设置起点坐标以及方向向量
for i=1:1:100
    L=i*i/100;
    R=i*i/100;
    A=pi*5/2+0.02;
    [xv,~,~]=draw_sline(xv,L,"on");%画直线
    [xv,~,~]=draw_sarc(xv,R,A);%画弧
end
axis equal;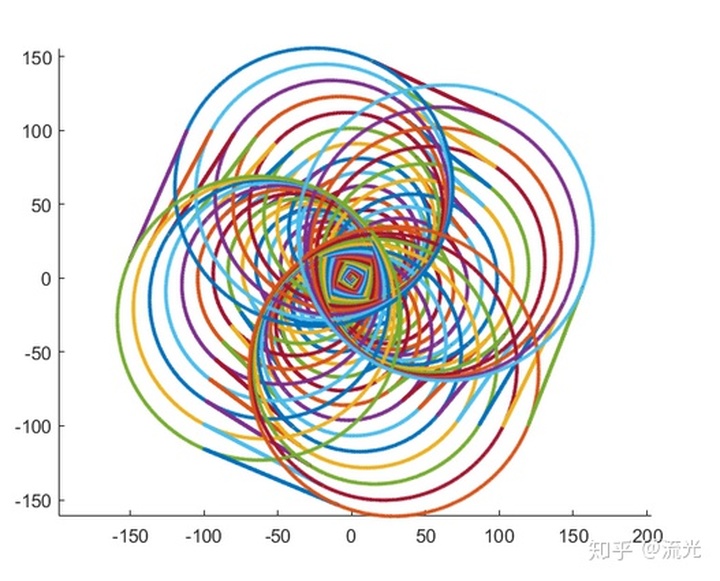

draw_sarc（）和draw_sline()这俩函数是自己写的，因为研究上的需要，有额外的功能，代码稍长，讲解可能没人愿意看就不贴在这里了，大家可以自己写一下，锻炼锻炼数学表达和编程能力，我写了一个Demo想了解的盆友可以自己下载

链接：https://pan.baidu.com/s/1yGSGcgQVzkFTipJwJA3enQ

提取码：i6xm

评论和私聊的都发了，不知道为什么被知乎系统检测有违规行为，评论也被删了很迷。。。