MATLAB的数学运算
- 多项式运算与插值
- 多项式的表示
- 多项式的四则运算
- 多项式的其他运算
- 数据插值方法
- 函数操作
- 函数的表示
- 函数文件的基本结构
- 数学函数图像的绘制
- **图像线性及颜色特征**
- 函数极值
- 一元函数的极小值
- 多元函数的极小值
- 函数的极大值
- fminbnd、fminsearch的区别
- 函数求解
- 数值积分
- 一元函数的积分
- 二重积分、三重积分
- 含参数函数的使用
- 1、用嵌套函数提供函数参数
- 2.用匿名函数提供函数参数
多项式运算与插值
多项式的表示
p
(
x
)
=
a
n
x
n
+
a
n
−
1
x
n
−
1
+
⋯
+
a
0
p(x)=a_n x^n + a_{n-1} x^{n-1} + dots + a_0
p(x)=anxn+an−1xn−1+⋯+a0
MATLAB中,上述多项式以向量
p
=
[
a
n
,
a
n
−
1
,
…
,
a
0
]
p=[a_n,a_{n-1},dots,a_0]
p=[an,an−1,…,a0]的形式存储的。它的系数是按降序排列。即n次多项式用一个n+1维向量表 示,缺少的幂次项系数为0。
可以用创建向量的方式创建多项式,再将其显示为多项式。
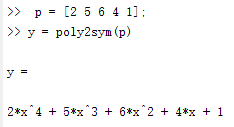
多项式的四则运算
多项式用向量来表示, 因此多项式的四则运算 可以转化为向量的运算:
- 多项式的加减: 对应项系数的加减;(在向量的加减中, 两个向量要有相同的长度)
- 多项式的乘法:多项式系数向量之间的卷积运算,可以通 过卷积函数conv来完成
- 多项式的除法:乘法的逆运算, 可以通过反卷积deconv来 实现
多项式的其他运算
| 函数名 | 作用 |
|---|---|
| roots | 多项式求根 |
| polyval | 多项式求值 |
| polyvalm | 矩阵多项式求值 |
| polyder | 多项式求导 |
| poly | 求矩阵的特征多项式 或求一个多项式,其根为指定的数值 |
| polyfit | 多项式曲线拟合 residue 求解余项 |
数据插值方法
插值运算是根据已有数据的分布规律, 找到一个函数表达式可以连接起已知的各点, 并用这一函数表达式 来预测已有数据两点之间任意位置上的数据。
一维插值由函数interp1实现:
y
i
=
i
n
t
e
r
p
1
(
y_i=interp1(
yi=interp1(
x
x
x,
y
y
y,
x
i
x_i
xi, method)
x,y分别为采用数据的x,y坐标,
x
i
x_i
xi为待插值的位 置,method为采用的插值方法;
y
i
y_i
yi为在
x
i
x_i
xi各点的插值结果
插值方法method:
| 参数 | 对应方法 |
|---|---|
| ‘nearest’ | 最邻近插值 |
| ‘linear’ | 线性插值 |
| ‘spline’ | 三次样条插值 |
| ‘pchip’ or ‘cubic’ | 三次插值 |
(nearest插值效果最差, 但计算简单省时. 其它三种方法差别不大)
x=[1 1.1 1.2 1.3 1.4]
y=[1.00000 1.23368 1.55271 1.99372 2.61170] %x,y的值
length_x = length(x)
xi = x(1):0.05:x(length_x)
length_xi=length(xi)
y_nearest=zeros(length(xi),1) %创建零数组
y_linear=zeros(length(xi),1)
y_spline=zeros(length(xi),1)
y_pchip=zeros(length(xi),1)
for i =1:length_xi
y_nearest(i)=interp1(x,y,xi(i),'nearest') %具体插值用法
y_linear(i)=interp1(x,y,xi(i),'linear')
y_spline(i)=interp1(x,y,xi(i),'spline')
y_pchip(i)=interp1(x,y,xi(i),'pchip')
end
函数操作
MATLAB提供了强大的函数操作功能, 包括函数图像 的绘制, 函数求极值和零点, 数值积分等, 这些函数 统称为”函数的函数”
函数的表示
MATLAB提供的函数表示方法:
一:利用M文件将函数定义为MATLAB函数;
二:采用匿名函数的方式。
y=@(x)exp(x)-x^5
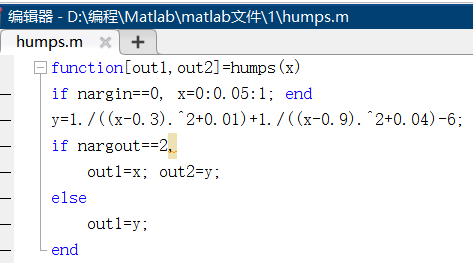
函数文件的基本结构

以function开头的一行为引导行,表示该M文件 是一个函数文件。
当输出形参多于一个时,应该用方括号括起来
关于函数文件名 函数文件名通常由函数名再加上扩展名.m组成。 当函数文件名与函数名不同时,Matlab将忽略函数名而确认文件名. 因此调用时使用函数文件名。
数学函数图像的绘制
函数fplot可以用来绘制数学函数的图像: fplot(fun,limits)
- fun:一个函数y=f(x), 可以是MATLAB函数的M文件名, 也可以是包含变量x的字符串, 还可以是函数句柄;
- limits:用于指定绘制图像的范围. [ x m i n x_{min} xmin, x m a x x_{max} xmax]指定x 轴的范围, [ x m i n x_{min} xmin, x m a x x_{max} xmax, y m i n y_{min} ymin, y m a x y_{max} ymax]同时指定x,y轴的范围;
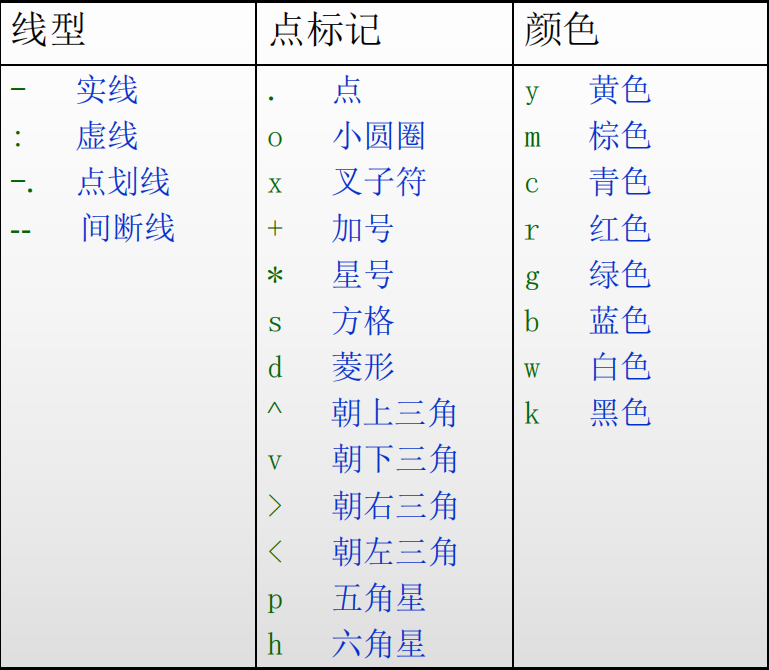
还可以指定线型和颜色(LineSpec),图像的相对精确度(tol),最少像点数(n).这些参数可以任意组合来控制图像的外观,如:
fplot(fun,limits,LineSpec)
fplot(fun,limits,tol)
fplot(fun,limits,tol,LineSpec)
fplot(fun,limits,n)
- 用[X,Y]=fplot(fun,limits)返回函数图形中各点的位置(一系列点的x,y值),但是不绘制函数图像
图像线性及颜色特征
函数极值
一元函数的极小值
可以使用函数fminbnd求得函数在给定区间上的局部极小值:
-------------------------x=fminbnd(fun,x1,x2,options)-------------------------------
fun为函数句柄,
x
1
,
x
2
x_1,x_2
x1,x2分别用于指定区间的左右边界, options用于指定程序的其他参数,用optimset实现
options的元素取值:
| 名称 | 描述 |
|---|---|
| Display | 控制结构的输出。参数off:不输出任何结果; iter:输出每个插值点的值;final:输出最后结果;notify:默认值,仅当函数不收敛时输出结果 |
| FunValCheck | 检测目标函数值是否有效。选择on:当函数返回的数据为复数或空数据时发出警告;off:不发出警告 |
| MaxFunnEvals | 允许进行函数评价的最大次数 |
| MaxIter | 最大迭代次数 |
| OutputFcn | 指定迭代时调用的用户自定义函数 |
| TolX | 返回 x x x的误差 |
-------------------[x,feval,exitflag, output] =fminbnd(fun,a,b)-----------------
fval(可省): 相应的极小值fval
exitflag(可省): 可以令函数返回程序停止的条件
| exitflag取值 | 对应程序停止的条件 |
|---|---|
| 1 | 函数在option.TolX条件下收敛到解x |
| 0 | 函数因为达到最大迭代次数或函数评价次数而结束 |
| -1 | 被输出函数停止 |
| -2 | 边界不一致( x 1 > x 2 x_1>x_2 x1>x2) |
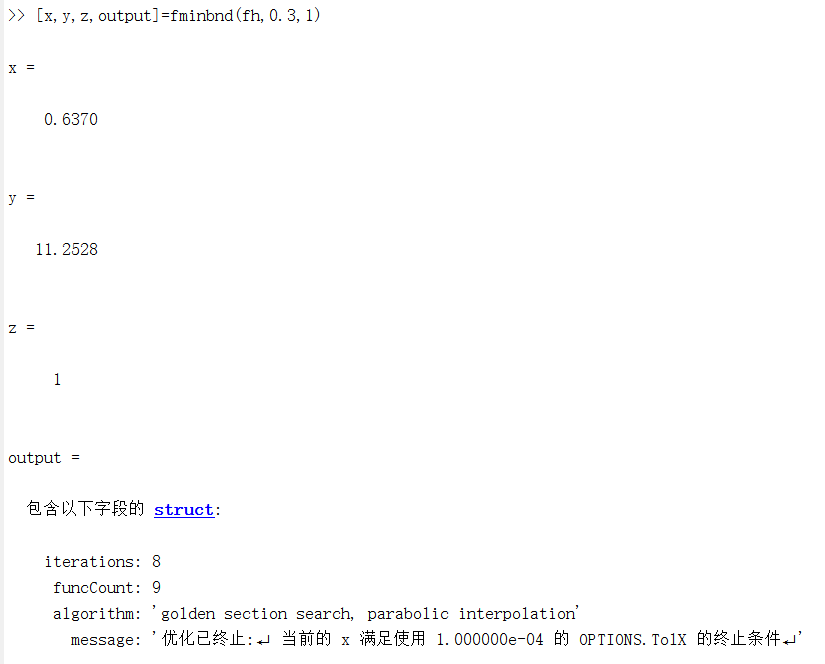
output(可省),作为一个结构体,其元素如下所示:
| 元素 | 表示内容 |
|---|---|
| output.algorithm | 采用的算法 |
| output.funcCount | 函数评价次数 |
| output.iterations | 迭代次数 |
| output.message | 退出信息 |

多元函数的极小值
函数fminsearch用于计算多元函数的极小值

具体操作同上一元函数的极小值
函数的极大值
对函数进行相反数处理,转化为函数求极小值
fminbnd、fminsearch的区别
- fminbnd的输入参数为寻找最小值的区间, 并且该函 数只能用于一维函数求极值
- fminsearch亦可以用来求一维函数的极值问题,其输入参数为初始值:fminsearch(@humps,0)
函数求解
函数fzero可以用来求一元函数的零点:
| 函数表达式 | 表达内容 |
|---|---|
| x=fzero(fun, x 0 x_0 x0) | 寻找x0附近fun的零点, 返回该点的x坐标 |
| x=fzeros(fun,[ x 1 , x 2 x_1,x_2 x1,x2]) | 寻找区间[ x 1 , x 2 x_1,x_2 x1,x2]内fun的零点, 返回该点的x坐标 |
| [x,fval]=fzero(…) | 返回零点的同时返回该点的函数值 |
| [x,feval,exitflag,output]=fzero(…) | 返回零点、函数值、程 序退出标志、选定的输出结果 |
数值积分
一元函数的积分
常用积分指令:quad和quadl。一般说来,quadl 比 quad 更有效。
具体调用格式如下: (quad用法和quadl一样)
q = quadl(fun,a,b)
q = quadl(fun,a,b,tol)
q = quadl(fun,a,b,tol,trace)
[q,fcnt] = quadl(fun,a,b,…)
输入量
前3个输入参数是调用积分指令所必须的,其他可以缺省
| 名词 | 表示意义 |
|---|---|
| fun | 被积函数的句柄 |
| a | 积分的下限,必须是确定的数值 |
| b | 积分的上限,必须是确定的数值 |
| tol | 一个标量,控制绝对误差 |
| trace | 为非0值时,将随积分的进程逐点画出被积分函数(跟踪迭代过程:计算函数值次数,当前积 分区间的左边界,步长,该区间内的积分值) |
输出参数fcnt返回函数的执行次数
二重积分、三重积分
常用积分指令:dbquad和triplequad
具体调用格式如下:
- q = dbquad(fun,xmin,xmax,ymin,ymax)
- q =dbquad(fun,xmin,xmax,ymin,ymax,tol)
- q=dbquad(fun,xmin,xmax,ymin,ymax,tol,method)
含参数函数的使用
1、用嵌套函数提供函数参数
编写M文件,该文件以函数参数为输入, 然后调用函数的函数来处理含参数函数,最后把含参数函数以嵌套函 数的方式包含在M文件中。
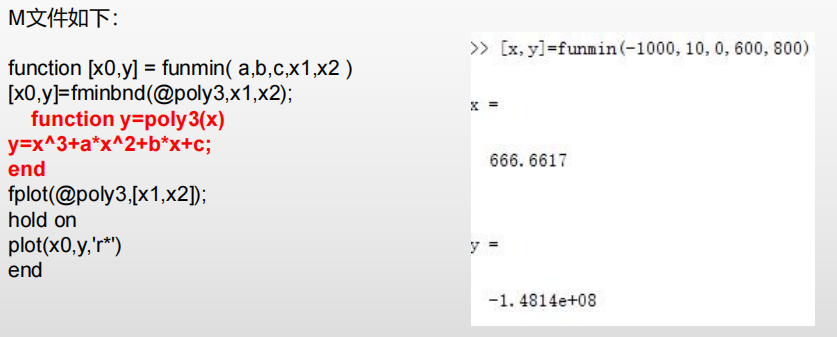
2.用匿名函数提供函数参数
首先创建一个含参数函数,保存在M文件, 输入参数为自变量和函数参数;用含参数函数创建匿名函数;把匿名函数 的句柄传递给函数的函数进行计算。
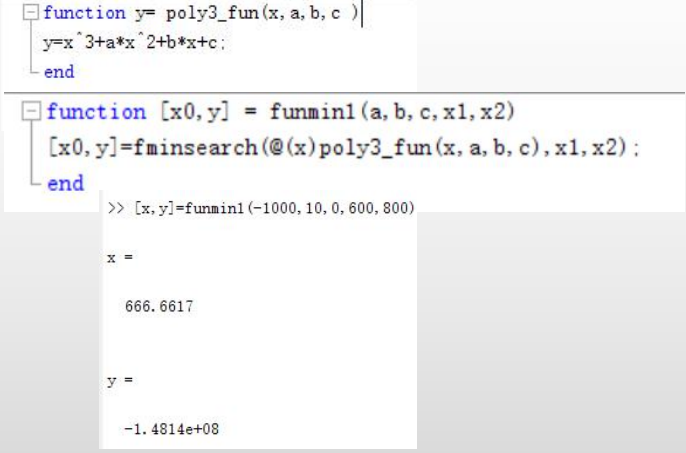
最后
以上就是彪壮大地最近收集整理的关于MATLAB的数学运算多项式运算与插值函数操作的全部内容,更多相关MATLAB内容请搜索靠谱客的其他文章。








发表评论 取消回复