问题提出：matlab如何求解方程的根？
符号方法求解:使用syms和sym创建符号变量
复制代码
1
2
3
4
5
6>> syms x x + x + x; (x + x + x)/4; >> x = sym('x'); x + x + x; (x + x + x)/4;
利用symbolic方法求解方程的根
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16>> syms x y = x*sin(x)-x; solve(y, x) ans = 0 pi/2 %或者 >> syms x solve(x*sin(x)-x) ans = 0 pi/2
2.
复制代码
1
2
3
4
5
6
7>> syms x y = cos(x)^2-sin(x)^2; solve(y, x) ans = pi/4
3.
复制代码
1
2
3
4
5
6
7>> syms x y = cos(x)^2+sin(x)^2; solve(y, x) ans = Empty sym: 0-by-1 %无解，等式不成立
solve()函数主要是用来求解代数方程 （多项式方程）的 符号解析解。也能解一些简单其他方程的数值解，不过对于解其他方程的能力很弱，此时求出的解往往是不精确或不完整的。注意可能得到的只是部分的结果，并不是全部解。
方程组求解
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15>> syms x y eq1 = x - 2*y - 5; eq2 = x + y - 6; A = solve(eq1,eq2,x,y); A.x %显示x的值 A.y %显示y的值 ans = 17/3 ans = 1/3
求解符号方程
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16>> %x为未知数，x默认为第一个被求解 syms x a b solve(a*x^2-b) ans = b^(1/2)/a^(1/2) -b^(1/2)/a^(1/2) >> %b为未知数 syms x a b solve(a*x^2-b, b) ans = a*x^2
练习：
复制代码
1
2
3
4
5
6
7>> syms x y a b r solve((x-a)^2+(y-b)^2-r^2) ans = a + (b + r - y)^(1/2)*(r - b + y)^(1/2) a - (b + r - y)^(1/2)*(r - b + y)^(1/2)
2.
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
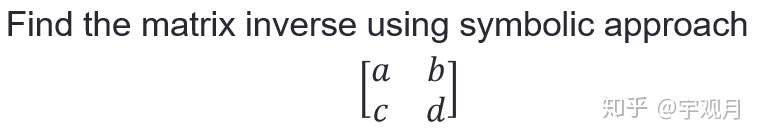
14>> syms a b c d A = [a b; c d] inv(A) A = [ a, b] [ c, d] ans = [ d/(a*d - b*c), -b/(a*d - b*c)] [ -c/(a*d - b*c), a/(a*d - b*c)]
符号微分
复制代码
1
2
3
4
5
6
7>> syms x y = 4*x^5; yprime = diff(y) yprime = 20*x^4
2.
复制代码
1
2
3
4
5
6
7>> syms x f(x)=exp(x^2)/(x^3-x+3); f1(x) =diff(f(x)) f1(x) = (2*x*exp(x^2))/(x^3 - x + 3) - (exp(x^2)*(3*x^2 - 1))/(x^3 - x + 3)^2
符号积分
复制代码
1
2
3
4
5
6
7
8>> syms x; y = x^2*exp(x); z = int(y); z = z-subs(z, x, 0) z = exp(x)*(x^2 - 2*x + 2) - 2
2.
复制代码
1
2
3
4
5
6
7>> syms x y = (x^2-x+1)/(x+3); int(y,[0, 10]) ans = log(302875106592253/1594323) + 10
函数句柄
构建函数
复制代码
1
2
3
4
5
6
7
8function [y] = xy_plot(input,x) % xy_plot receives the handle of a function and plots that % function of x y = input(x); plot(x,y,'r--'); xlabel('x'); ylabel('function(x)'); end
调用函数
复制代码
1xy_plot(@sin,0:0.01:2*pi);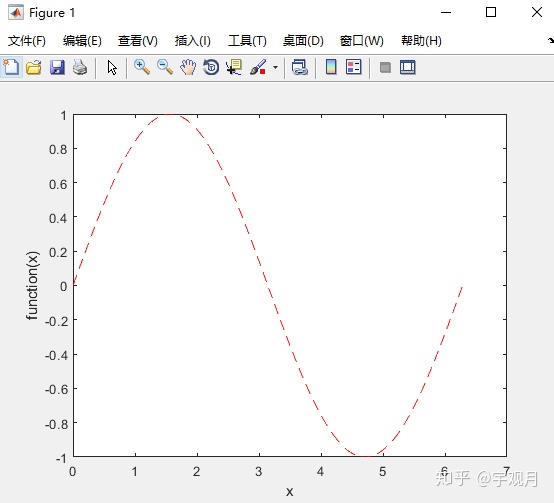
创建函数句柄
复制代码
1
2
3
4
5f2 = @(x) (1.2*x+0.3+x*sin(x)); %创建函数句柄 fsolve(f2,0) %求解方程根，f2为函数句柄，0为猜测根 ans = -0.350026819561814
fzero()求解非线性方程的根
x=fzero(fun,x0)tries to find a pointxwherefun(x) = 0. This solution is wherefun(x)changes sign—fzerocannot find a root of a function such asx^2.
复制代码
1
2
3
4
5
6>> f=@(x)x.^2; fzero(f,0.1) ans = NaN
x=fzero(fun,x0,options)usesoptionsto modify the solution process.
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18>> f=@(x)x.^2 options=optimset('MaxIter',1e3,'TolFun',1e-10); %迭代次数与误差 fsolve(f,0.1,options) fzero(f,0.1,options) f = 包含以下值的 function_handle: @(x)x.^2 ans = 1.953199358881746e-04 ans = NaN
roots()求解多项式函数的根
复制代码
1
2
3
4
5
6
7
8
9>> roots([1 -3.5 2.75 2.125 -3.875 1.25]) ans = 2.000000000000005 + 0.000000000000000i -1.000000000000000 + 0.000000000000000i 0.999999999999999 + 0.500000000000000i 0.999999999999999 - 0.500000000000000i 0.499999999999999 + 0.000000000000000i
- roots()只能用于求解多项式
复制代码
1
2
3
4
5
6
7>> roots([1 -6 -12 81]) ans = -3.596915527892119 5.509725948409570 4.087189579482555
matlab如何求解这些函数根的？
主要有两种方法：不断迭代，直到满足精度和迭代次数，求解出方程根。
- 二分法（bisection method）
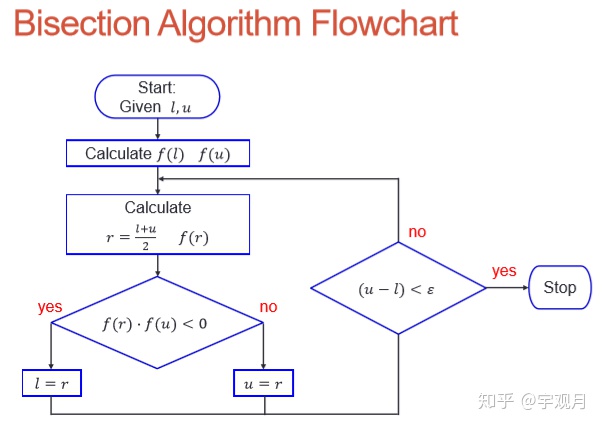
2. 牛顿-拉夫森迭代法（Newton-Raphson method）
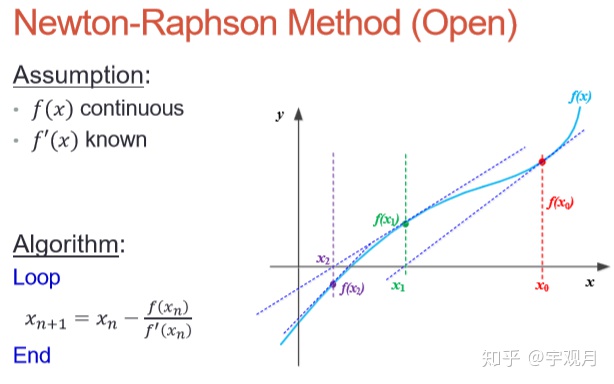
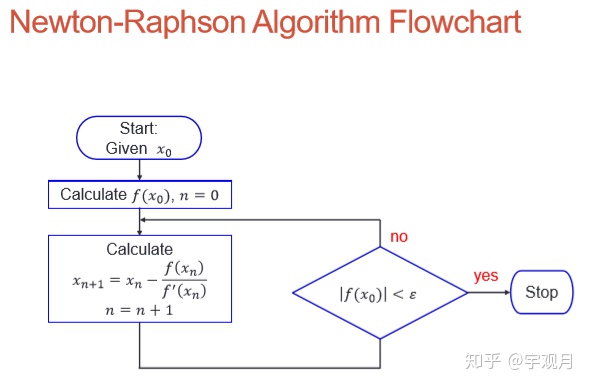
二者比较
声明：
此笔记是通过观看台大郭彦甫老师的视频教程学习总结而来，想着边学习边记录，方便今后查阅。原视频教程见：
https://www.youtube.com/playlist?list=PLVHBjRDK0kALcQMwAFbR5q2driYZCHNIxwww.youtube.com最后
以上就是过时水池最近收集整理的关于数值计算方法 matlab用二分法或简单迭代法求_MATLAB学习笔记-11方程根的求解的全部内容，更多相关数值计算方法内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
发表评论 取消回复