双 JK 触发器 74LS112 逻辑功能。真值表_数字电路学习笔记（十一）：时序逻辑...

时序逻辑将会是本笔记的最后几章的主题。虽然数字电路课程还包括脉冲电路、模数转换、EDA等内容，但那些和本文的主线内容（不注重硬件搭建的电路设计）关系就不大了。

一、时序功能

我们从一个例子开始，说明时序逻辑的概念和作用。

设计一个电路，当连续输入四个及以上的高电平时，输出高电平；其他时候，输出低电平。

这个需求显然无法用我们已设计过的任何组合逻辑电路实现：因为对于组合逻辑，每一次工作都是独立的，“连续输入四个高电平”这样的场景无法出现（但是，我们可以做出一个检验“同时输入四个高电平”的电路；品味这其中的区别）。因此，我们需要借助时序电路的时序功能。

时序电路和组合逻辑电路类似，我们最为关心的是它的输入（命名为

）和

），在此题中，已经有了良定义的输入输出；同时，时序逻辑电路还会拥有一组自身的

。当

时，每次输入一个高电平，即认为已经“连续输入了四个以上的高电平”，输出高电平；其他时候，则根据输入决定是状态+1还是状态归0。这样的文字表述，我们可以用这样一张状态转换图做可视化：

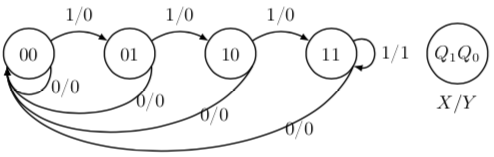
在前两章中，已经出现了一些简单的状态转换图。为了理解这张图，我们首先确定电路的初始状态——在此图中，是最左边的00的圈；接着，顺着箭头，看状态是如何变化的。每个箭头上都写着状态转换所对应的输入输出——至于具体的对应，要看右边的图例，比如此处就标明，斜杠左边为输入

，右边为输出

。如果我们在状态为00时输入1，则跳转到01状态；否则保持00状态。接下来每次输入1，则跳转到下一个状态；输入0，则跳转回00。但对于以上所有状态转换，输出都是0。直到状态变成11时，才会在输入1时输出1。

观察状态转换图，发现每个状态的“指入箭头”数目不定，但“指出箭头”数目在输出位数为

时一定是

（可以重合）。否则，就会有“未定义的状态转移”。

对于时序逻辑电路的分析，和对有限状态机 (Finite state machine) 是一样的。事实上，可以把时序逻辑电路看作有限状态机的一种实现形式，许多有限状态机的概念也可以运用到电路中来。可以以下面这篇文章为参考。

二、时序逻辑电路的信息流

对一个电路的整体功能有了理解之后，我们可以进一步研究在这个系统中的信息流动。（注意，在这一部分，我们并不关注电路的实际实现，而是从更高、更抽象的观点研究它。）

时序逻辑电路可以分为两部分：存储电路和组合逻辑电路。组合逻辑和时序逻辑与其说是“平行关系”，不如说是“继承关系”。如果组合逻辑电路可以用下图表示（见笔记（六）：组合逻辑电路）：

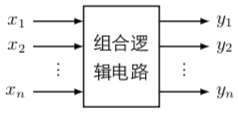
那么时序逻辑电路不过是再加一个辅助的存储电路：

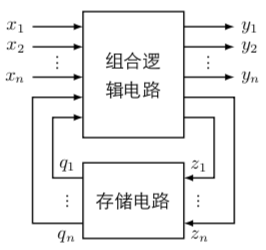
其中

以及

是我们熟悉的输入

和输出

。事实上，应该是向量形式的

和

，但没有必要做这种区分，造成更多的困惑。

实际输入存储电路的并不是输入本身，而是已经经过处理的内部输入信号

。它控制了由锁存器和触发器组成的存储电路。存储电路又会产生

，也就是它的状态。

回忆组合逻辑电路的方程，我们给出了一般形式

，表示输出完全由输入决定。对于时序逻辑，我们定义如下三组方程（我花了点时间试着通过例子来合理化这些方程，但最后发现还是直接把它们作为定义更合理。在后续的实际电路设计中，能对它们的意义有更好地理解）：

这些方程可以通过上图得出。

注意，状态并不是实时更新的——不然可以想见，由于有

，对于任何一个输入，状态一定会落到一个

的稳态上，但这种稳态的数量是非常有限的。事实上，时序逻辑电路的存储电路仍由时钟信号控制，只有在一个时钟信号的边沿发生单次状态更新。

还有两个概念可以在这里提出：

• 由于存储电路由不止一个触发器构成，每个触发器都需要一个时钟信号，这些时钟信号可以由同一个信号源给出，同时更新，也可以分别更新。前者称为同步电路，后者称为异步电路。下文中所有电路都为同步电路。
• 有些电路没有外部输入信号，而完全依靠时钟信号进行状态更新；另一些的输入信号只影响状态，而不决定输出。对于两种情况，输出都只与状态有关（
  ）。这种电路称为Moore型电路。而
  的则称为Mealy型电路。

这一节非常抽象，提出了很多定义和公式。事实上，第一遍学习时不完全理解问题不大，但通过后续逐步介绍的电路设计，可以对时序逻辑有更深刻的认识。

三、时序电路的功能表示

1、状态转换表

在组合逻辑中，我们用真值表对功能做了最具象的表达。对于时序逻辑，虽然需要同时研究输入、输出和状态的相互作用关系，但真值表也可以达到同样的效果。在时序逻辑中，真值表叫做状态转换表。

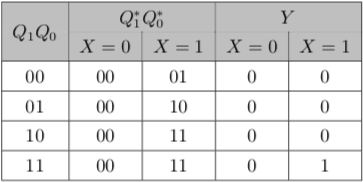
通过该真值表，我们可以用一样的思路列出各个方程。

上图可能和一般的真值表有稍许不同——因为我们把

的值横向排列而不是像一般的做法一样纵向排列，这样可以缩短表格长度，也更加强调“状态转换”的关系。但是画成下图这样也是一样的：

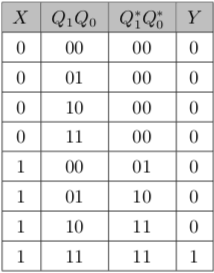
2、状态转换图

在时序逻辑设计中，状态转换图是比转换表更加直观的表示方法。就像之前给出的示例一样：

从一张图上，就可以读出许多输入/输出/状态的对应关系，对于它们之间的影响关系也要比转换表直观。因此，它一般是逻辑设计的第一步，而后再根据该图填写转换表或卡诺图，列方程。

3、卡诺图

令我绘制得非常痛苦的一类图表。也可以表示输出和次态是如何受输入和现态影响的。由于在时序逻辑中有较多的无关项（具体例子会在后文给出），卡诺图可以极大地方便列方程的过程。

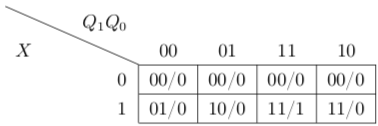
4、状态方程

也就是之前列出的三组方程：

当我们成功列出方程后，离设计实际电路就只有一步之遥了。

以上便是几种常用的时序逻辑电路功能表示方法。它们都是在绘制电路前不可缺少的步骤，也是理解电路功能必需的工具。

本章非常抽象，我也花了很大功夫试图合理化抛出的每个概念。但4个月后，我仍然对我的成果不满意。希望各位可以提出你们的意见，并感谢各位在我断更的四个月内对我的支持:)