异步八进制减法计数器分析

68 阅读 0 评论 45 点赞

我是靠谱客的博主诚心小甜瓜，最近开发中收集的这篇文章主要介绍异步八进制减法计数器分析，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

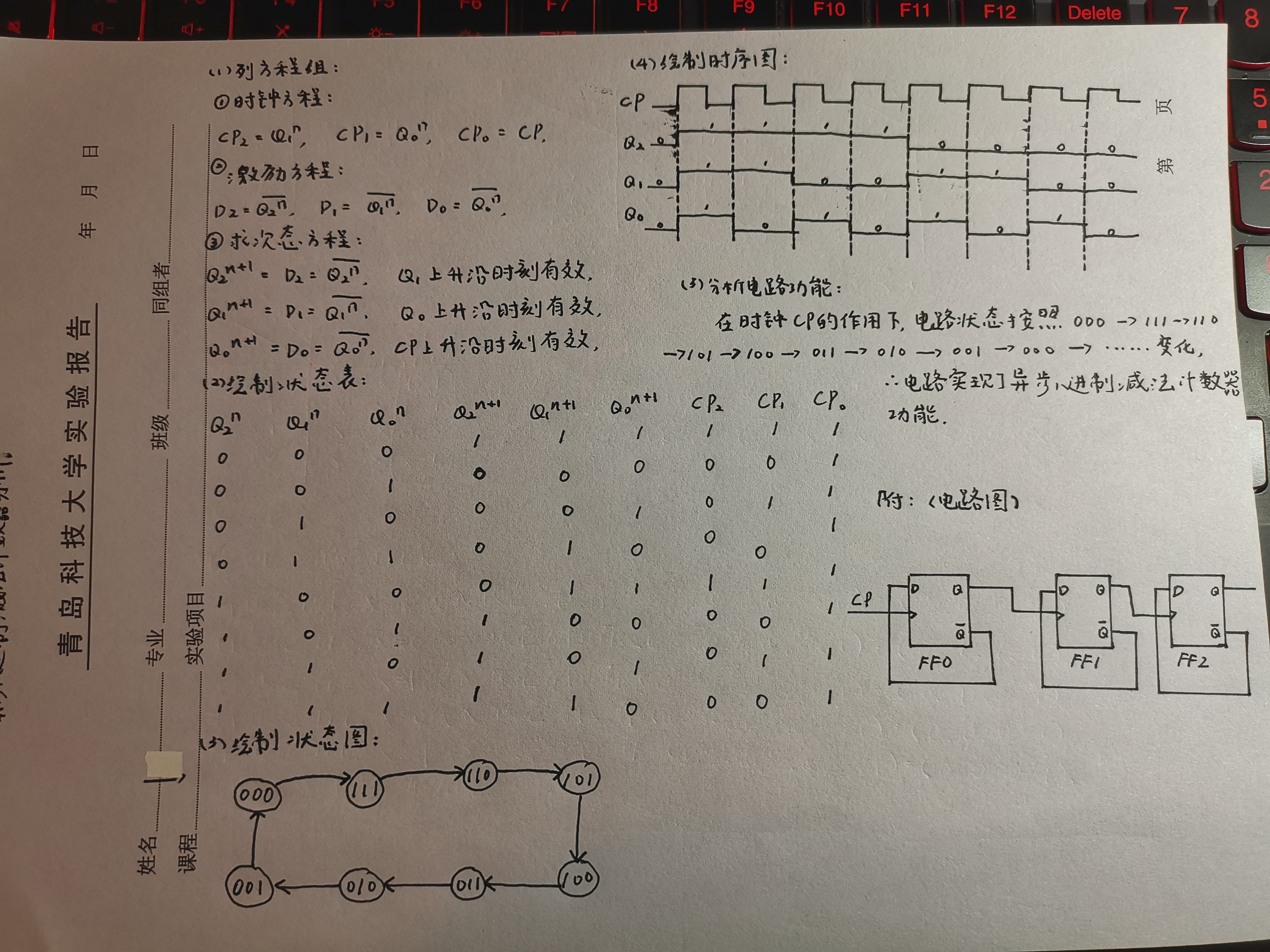
异步时序逻辑电路分析步骤:

(1)列方程组:

①时钟方程, ②激励方程, ③次态方程.

(2)绘制状态表.

绘制状态表时的思路与同步时序逻辑电路有些许不同: 要根据每个触发器的时钟方程来填充状态表. 以这里的分析过程举例. $CP_{0}$ 、 $CP_{1}$ 、 $CP_{2}$ = 1时, 表示时钟有效; 否则时钟无效. 由于0#触发器的时钟信号引脚直接接到系统的时钟信号线上, 故0#触发器和系统时钟CP保持一致: 这是求次态的突破口. 这样一来, 系统 $CP$ 有效时, $CP_{0}$ 也有效, 所以 $CP_{0}equiv 1$ . 既然 $CP_{0}$ 一直有效(当系统时钟CP有效时), 那么就按照次态方程求出所有的 ${Q_{0}}^{n+1}$ . 之后, 根据 $CP_{1}={Q_{0}}^{n}$ , 得知只有在 $Q_{0}$ 上升沿时, $Q_{1}$ 才按照触发器次态方程进行状态转换: 其他时刻数据保持不变. 如此一来, 就可以求出所有的 ${Q_{1}}^{n+1}$ . 再根据 $CP_{2}={Q_{1}}^{n}$ , 得知只有在 $Q_{1}$ 上升沿时, $Q_{2}$ 才按照触发器次态方程进行状态转换: 其他时刻数据保持不变. 综上所述, 状态表填充完毕. 值得一提的是, 对于状态表中的某一行, 现态到次态的变化时刻为系统时钟的有效时刻(这里 $Q_{0}$ 的变化时刻和系统时钟有效时刻吻合, 但 $Q_{1}$ 、 $Q_{2}$ 的变化会相应滞后): 若三个触发器的状态都要发生改变 ,则状态改变的先后顺序为 $Q_{0}->Q_{1}->Q_{2}$ , 这期间会有一定的时间消耗.