带通滤波器中心频率计算公式中R是哪个值_手把手教系列之IIR数字滤波器设计实现...

喜欢就本文就点个赞吧～～

版权声明：所有文章版权归嵌入式客栈所有，如商业使用，须嵌入式客栈授权。欢迎关注微信公众号，内容更丰富。

【导读】：在嵌入式系统中经常需要采集模拟信号，采集模拟信号的信号链中难免引入干扰，那么如何滤除干扰呢？今天就来个一步一步描述如何设计部署一个IIR滤波器到你的系统。写这篇文章考虑到很多粉丝是做单片机系统开发的，经常会需要采集模拟信号，系统中往往存在各种各样的干扰，干扰常常让人一筹莫展，所以花了一周时间整理出IIR滤波器设计部署的干货文章，照此一步一步做，你必会解决大部分干扰问题。

编外语：文章写作过程虽谈不上呕心沥血，但也可算绞尽脑汁。在此也呼吁粉丝朋友积极参与互动，或点在看，或分享，或留言评论！如果大家对此类话题感兴趣，我会写出系列信号处理文章以答谢各位的厚爱，如果大家对此类话题不感兴趣，就不在花过多时间整理发布了。在此感谢各位关注厚爱

何为IIR滤波器？

无限冲激响应（IIR：Infinite Impulse Response）是一种适用于许多线性时不变系统的属性，这些系统的特征是具有一个冲激响应h（t），该冲激响应h（t）不会在特定点上完全变为零，而是无限期地持续。这与有限冲激响应（FIR：Finite Impulse Response）系统形成对比，在有限冲激响应（FIR）系统中，对于某个有限T，在时间t> T时，冲激响应确实恰好变为零。线性时不变系统的常见示例是大多数电子和数字滤波器。具有此属性的系统称为IIR系统或IIR滤波器。对于什么叫冲激响应，这里就不展开解释了，有兴趣的可以查阅相关书籍。

这是常见的教科书式数学严谨定义，很多人看到这一下就蒙了，能说人话吗？

线性时不变系统理论俗称LTI系统理论，源自应用数学，直接在核磁共振频谱学、地震学、电路、信号处理和控制理论等技术领域运用。它研究的是线性、非时变系统对任意输入信号的响应。虽然这些系统的轨迹通常会随时间变化（例如声学波形）来测量和跟踪，但是应用到图像处理和场论时，LTI系统在空间维度上也有轨迹。因此，这些系统也被称为线性非时变平移，在最一般的范围理论给出此理论。在离散（即采样）系统中对应的术语是线性非时变平移系统。由电阻、电容、电感组成的电路是LTI系统的一个很好的例子。比如一个运放系统在一定频带范围内满足信号的时域叠加，输入一个100Hz和200Hz正弦信号，输出频率是这两种信号的线性叠加。

用数学对LTI系统描述：

线性：输入x1(t)，产生响应 y1(t),而输入x2(t),产生相应y2(t) , 那么放缩和加和输入 ax1(t)+bx1(t), 产生放缩、加和的响应ay1(t)+by1(t)，其中a和b是标量，对于任意的有：

输入

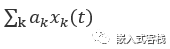
产生响应为：

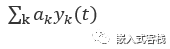
时不变性：指如果将系统的输入信号延迟δ秒，那么得到的输出响应也相应延时δ秒。用数学描述，也即如果输入x1(t),产生响应y1(t) ，而输入x1(t+δ) ，产生响应 y1(t+δ)。
这么描述还是不易懂，来个图，有图有真相：

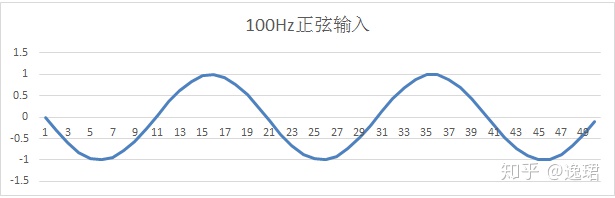
假定一个信号放大电路对100Hz正弦信号放大2倍：则输出为：

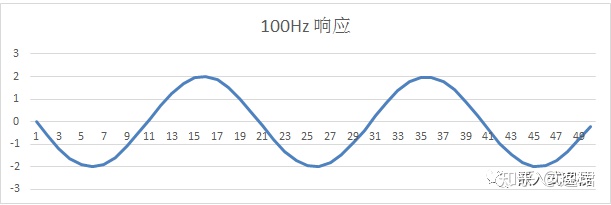
而对200Hz的正弦信号，假定其放大倍数为1.7倍。（做过运放电路设计的朋友应该有经验，在其同频带其放大倍数往往并不平坦，也即幅频响应在频带内不平坦，这是比较常见的）。也即输入为：

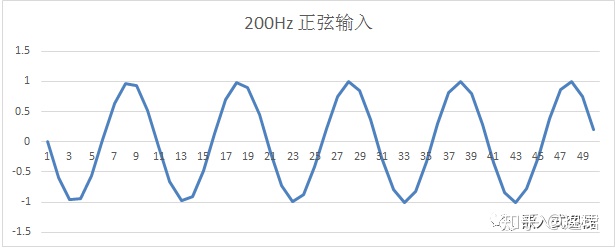
则输出波形为：

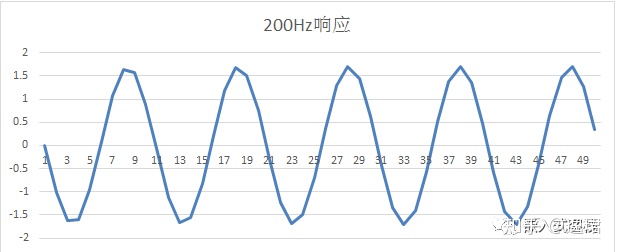
那么如果输入100Hz和200Hz的时域叠加信号，则其输入为：

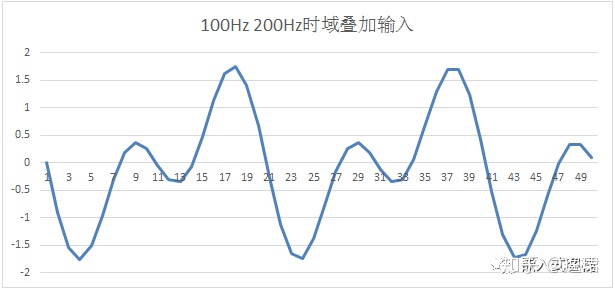
则其响应为：

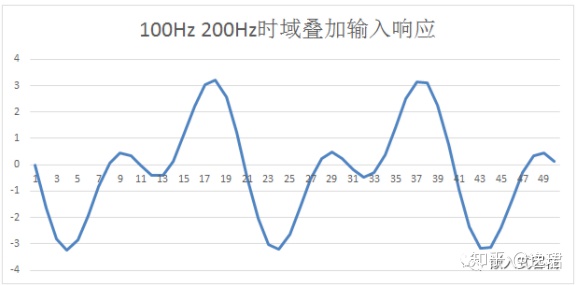
上面这么多文字只是为了描述在什么场合可以使用IIR滤波器对信号进行数字滤波。总结而言，就是在线性时不变系统中适用。换言之，在大多数电路系统中我们都可以尝试采用IIR滤波器进行数字滤波。

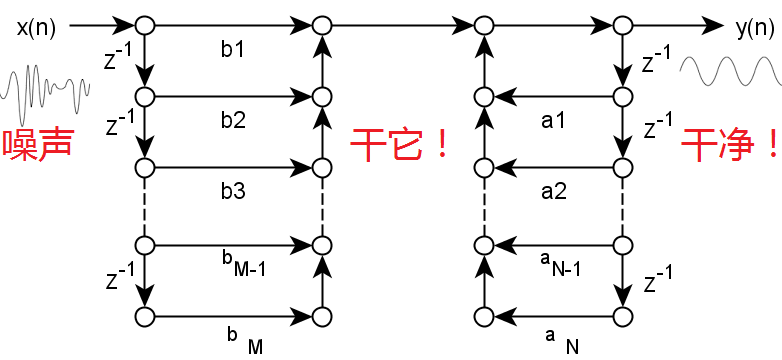
那么究竟什么是IIR滤波器呢？从数字信号处理的书籍中我们能看到这样的Z变换信号流图：

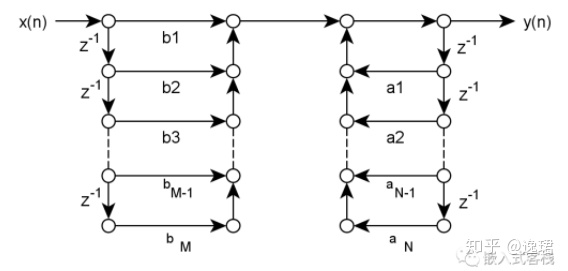
Z的-1次方表示延迟一拍,在数字系统中表示对于输入信号而言,即为上一次采样值,对于输出而言,即为上一次的输出值。

在时域中对于上述流图，用时域描述即为：

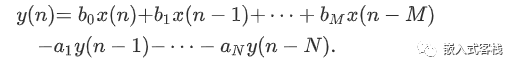
上述数字滤波器，如果从编程的角度来看，x(n-1),表示上一次的信号，可能是来

如果熟悉Z变换，则Z变换传递函数为：

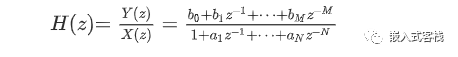
上述数字滤波器，如果从编程的角度来看，x(n-1),表示上一次的信号，可能是来自ADC的上次采样，而y(n-1)则为上一次滤波器的输出值，对应就比较好理解x(n-N)就表示前第n次输入样本信号，而y(n-M)则为前第M次滤波器的输出。

说了这么多，只是为了更好的理解概念，只有概念理解正确，才能使用正确。概念理解这对工程师而言，非常之重要。

如何设计呢？

MATLAB提供了非常容易使用的FDATool帮助我们设计数字滤波器，真正精彩的地方开始了，让我们拭目以待究竟如何一步一步设计并实施一个IIR滤波器。首先打开MATLAB,在命令行中敲fdatool，然后敲回车

弹出窗体就是fdatool了，如下：

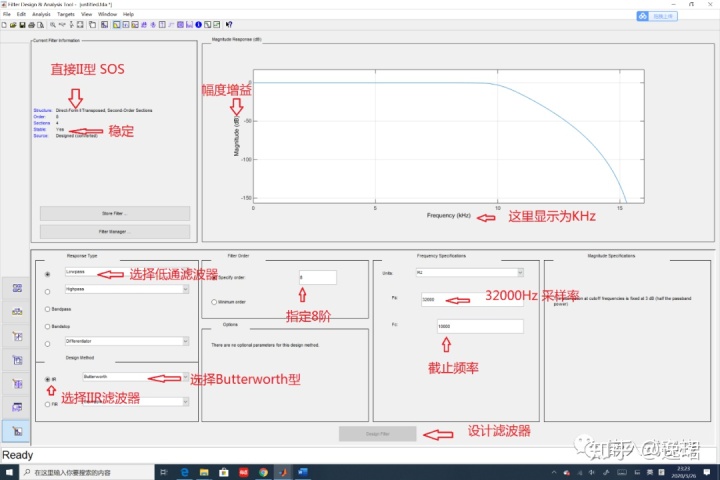
在设计具体,有几个相关概念需要澄清：Fs：采样率，单位为Hz,真实部署在系统中，请务必确保样本是按照恒定采样率进行采样，否则将得不到想要的效果。Fpass: 通频带，单位为Hz,即系统中期望通过的最高频率。Fstop: 截至频率，即幅频响应的-3dB处的频率，这个如不理解，请自行查阅相关书籍。分贝dB: 这是一个无单位反应输出与输入倍数的一个术语。电学中分贝与放大倍数的转换关系为：

• A(V)(dB)=20lg(Vo/Vi)；电压增益,Vo 为输出电压，Vi为输入电压
• A(I)(dB)=20lg(Io/Ii)；电流增益,Io 为输出电流，Ii为输入电流
• A(p)(dB)=10lg(Po/Pi)；功率增益，Po 为输出功率，Pi为输入功率

滤波器类型：这里有Butterworth(巴特沃斯)、Chebyshev Type I,Chebyshev Type II、(切比雪夫)、Elipic 等可选。

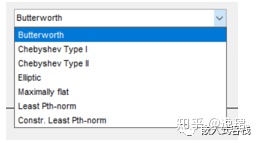
• 巴特沃斯 Butterworth，也被称作最大平坦滤波器。巴特沃斯滤波器的特点是通频带内的频率响应曲线最大限度平坦，没有纹波。
• 切比雪夫 Chebyshev，是在通带或阻带上频率响应幅度等波纹波动的滤波器。切比雪夫滤波器在过渡带比巴特沃斯滤波器的衰减快，但频率响应的幅频特性不如后者平坦。
• 椭圆 Elliptic，椭圆滤波器是在通带和阻带等波纹的一种滤波器。
• …这里就不一一介绍了，有兴趣可以去查信号处理书籍。

就其特点，这里对其中几种略作介绍：

• 巴特沃斯具有最平坦的通带。
• 椭圆滤波器衰减最快，但是通带、阻带都有波纹。
• 切比雪夫滤波器衰减比巴特沃斯快，但比椭圆滤波器慢，波纹区域可选择。

假设我们需要设计一个IIR滤波器，采样率为32000Hz, 有用信号频率在10000Hz内，设计IIR滤波器对信号进行数字滤波。这里为节省算力，我们指定滤波器的阶数，也即传递函数中N/M中的最大值，一般而言N大于M。

这里指定阶数为8阶，类型指定为巴特沃斯型IIR滤波器，输入阶数8阶，采样率32000Hz,然后点击Design Filter如下图所示：

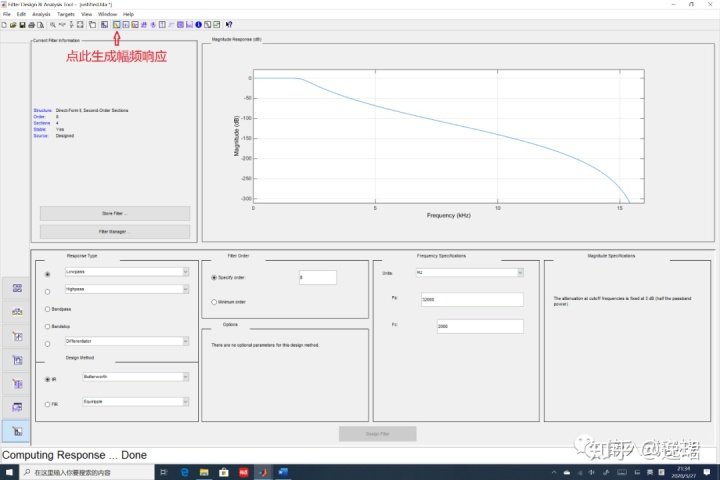
其相频响应曲线如下：

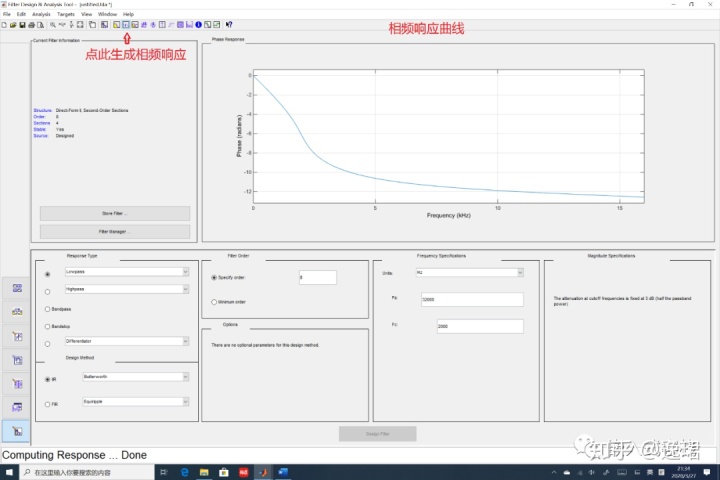
除此之外，我们还可以将幅频与相频曲线放在一个频率坐标上去看设计结果：

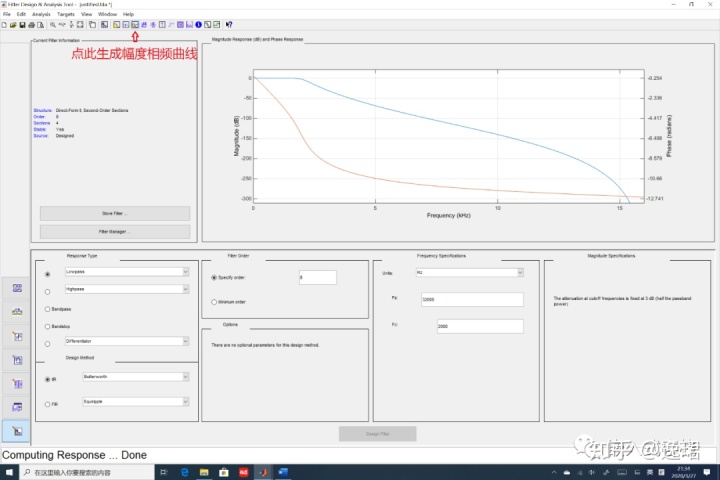
导出滤波器参数，这里我们选择，然后就得到了一个文件，保存2KHz_LPF.fcf，文件名随你喜欢。

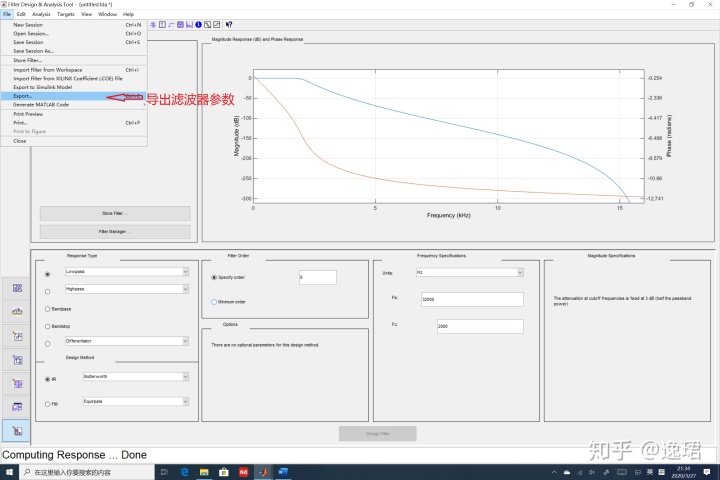
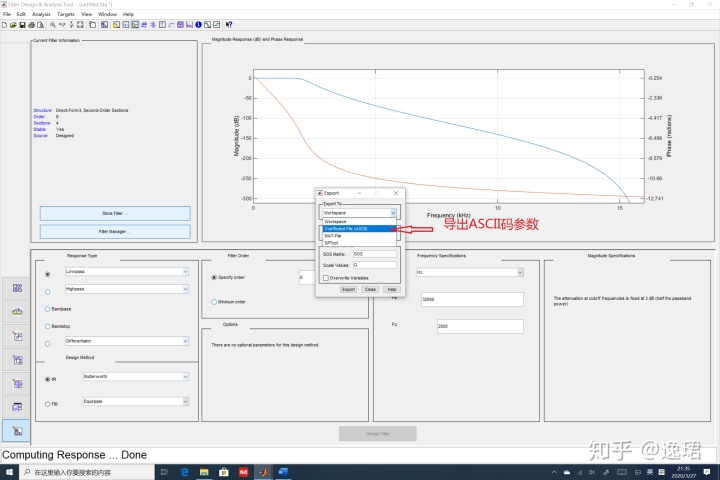
文件内容如下：

% Generated by MATLAB(R) 8.4 and the Signal Processing Toolbox 6.22.
% Generated on: 27-Mar-2020 21:27:06

% Coefficient Format: Decimal

% Discrete-Time IIR Filter (real)                            
% -------------------------------                            
% Filter Structure    : Direct-Form II, Second-Order Sections
% Number of Sections  : 4                                    
% Stable              : Yes                                  
% Linear Phase        : No                                   


SOS Matrix:                                                  
1  2  1  1  -1.7193929141691948  0.8610574795347461          
1  2  1  1  -1.5237898734101736  0.64933827386370635         
1  2  1  1  -1.4017399331200424  0.51723237044751591         
1  2  1  1  -1.3435020629061745  0.45419615396638446         

Scale Values:                                                
0.035416141341387819                                         
0.031387100113383172                                         
0.028873109331868367                                         
0.027673522765052503                                          

至此设计工作就结束了，马上进入滤波器的部署测试阶段。

这里有个概念需要略作解释：什么叫直接II型 SOS 二阶块

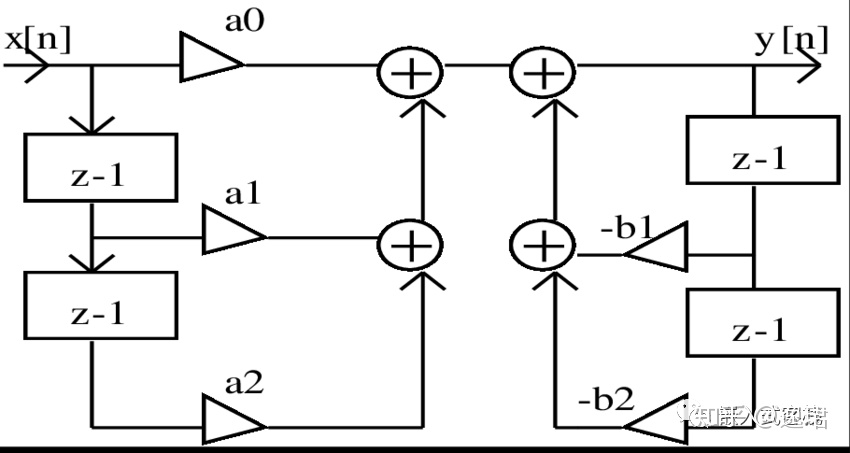
所谓直接II型，SOS（second order section）理解很简单，本质是将IIR Z传递函数分解为上述二阶块的级联形式。

部署测试滤波器

到这里，没有经验的朋友可能会说，这么一堆参数我该咋用呢？

需要自己去写前面描述的计算公式吗？当然你也可以这么做，这里就不写了,ARM的CMSIS库已经帮大家设计好了种类繁多的数字信号处理函数实现了，而且经过了测试，这里直接拿来用即可。有兴趣自己写也不难，只要理解Z传递函数概念内涵，非常容易实现。这里我们采用32位浮点实现函数：

arm_biquad_cascade_df1_f32。该函数位于：

CMSISDSPSourceFilteringFunctionsarm_biquad_cascade_df1_init_f32.c中

以及CMSISDSPSourceFilteringFunctionsarm_biquad_cascade_df1_f32.c

我们来看一看这个函数：

arm_biquad_cascade_df1_init_f32.c：

/*

arm_math.h 定义了须用到的结构体，对于本例相关的结构体为arm_biquad_casd_df1_inst_f32

typedef 

滤波器具体滤波函数为arm_biquad_cascade_df1_f32

/**

开始测试：

#include 

利用csv文件，将模拟数据存储，直接用excel打开，将行数据生成曲线图如下：

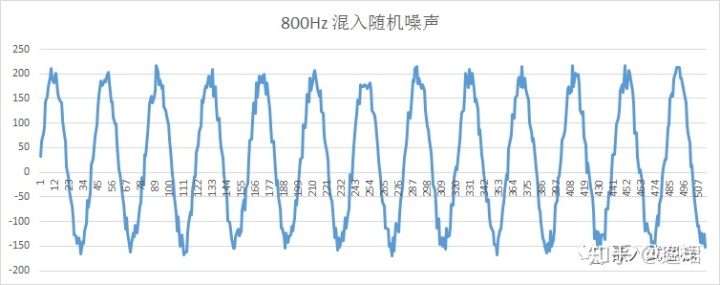
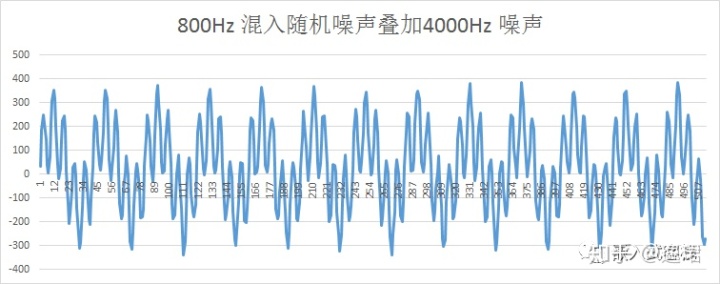
• 第一幅图，为800Hz信号混入随机噪声的波形
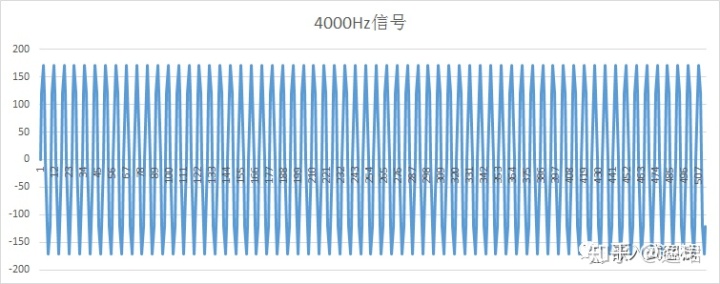
• 第二幅图，为4000Hz信号，对假定系统为无用干扰信号
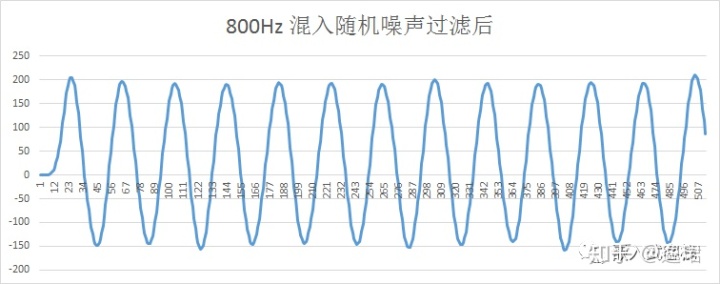
• 第三幅图， 为800Hz 混入随机噪声过滤后，已经很好的还原有用信号频率
• 第四幅图， 为800Hz信号混入随机噪声，同时叠加4000Hz干扰的波形，对系统而言，从时域中，明显可见，有用信号已经完全扭曲
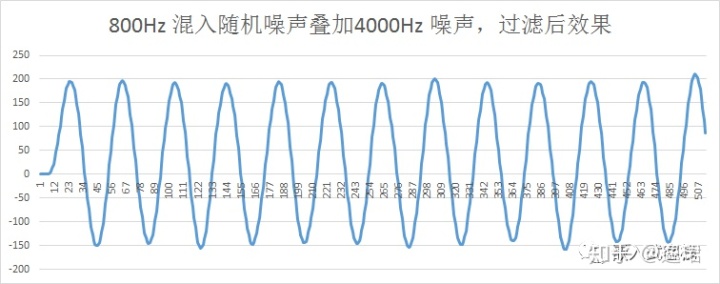
• 第五幅图，为800Hz信号混入随机噪声，同时叠加4000Hz干扰的输入，经过该低通滤波器后的波形，与第三幅图基本一样，已经非常好的滤除了干扰信号。

总结：

• IIR滤波器在线性时不变系统中可以很好的解决工程中一般噪声问题
• 如果需要设计带通、高通滤波器其步骤基本类似，只是滤波器的参数以及SOS块个数可能不一样而已
• 需要提醒的时，IIR的相频响应不线性，如果系统对相频响应有严格要求，就需要采用其他的数字滤波器拓扑形式了
• 实际应用中，如果阶数不高时，现在算力强劲的单片机或者DSP以及可以直接使用浮点处理。
• 如果对处理速度有严格的实时要求，需要在极短时间进行滤波处理，可以考虑降低阶数，或采用定点IIR滤波算法实现。也或者将文中函数进行汇编级优化。

版权声明：所有文章版权归嵌入式客栈所有，如商业使用，须嵌入式客栈授权。

如喜欢本文就点个关注，或者微信扫一扫，关注公众号