本节来说一下傅里叶变换的概念和定理。
傅里叶变化起源于热学,在当今社会主要应用于数字通信领域,它可分析信号的成分,也可用这些成分合成信号。在其他领域,特别是光学领域,傅里叶变化也有着极其广泛的应用。在本节中,我们会详细阐述傅里叶级数、傅里叶变换的基本概念以及其基本定理。
一、傅里叶级数
1、三角傅里叶级数
利用三角函数系在区间
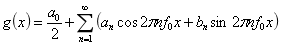
该函数应该满足狄利赫里条件,即一个周期内只有有限个极值点和第一类不连续点。其中
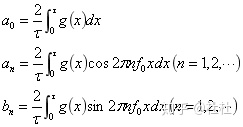
对于偶函数,只保留余弦函数项,对于奇函数,只保留正弦函数项。
2、指数傅里叶级数
满足狄利赫里条件的周期函数
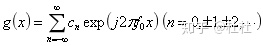
其傅里叶系数可写作:
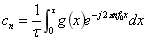
根据欧拉公式,我们不难推出指数型傅里叶级数系数与三角傅里叶级数系数之间的关系。推导如下:
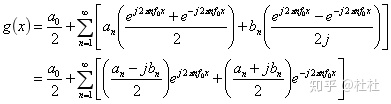
若令
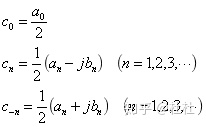
则有
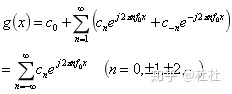
在复指数傅里叶级数中,
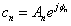
式中,
傅里叶级数可以用来表示周期函数。对于周期趋于无穷大,即非周期函数时,基频趋于零,频率取值不再是离散的,而是连续的,此时我们也可以采用傅里叶分析,即傅里叶变换。
二、傅里叶变换
1、基本概念
定义式 :复函数
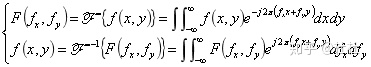
式中
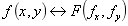
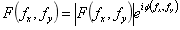
傅里叶变换成立的充要条件为:
(1)函数在
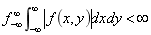
(2)函数在xoy全平面上每一个有限区域内局部连续,仅存在有限个间断点。
(3)函数没有无限大间断点。
但是,某些函数却无法满足上述存在条件中的某一条或多条,因此有必要对上述傅里叶变换定义作推广,即广义傅里叶变换,常见的这样的函数有:
设存在函数
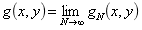
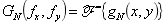
则令
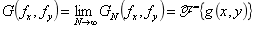
换言之,函数
由逆变换式,,可以把函数
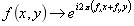
此时可以发现,其频谱只不过是一个权重因子。
这种基元函数具有下述性质:
(1)由于在xoy平面上传播的平面波,其复振幅可以表示为:
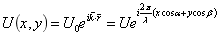
故基元函数代表传播方向为如下的单位振幅平面波:
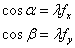
(2)当
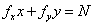
有
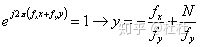
在这些直线上位相为零或者
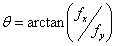
为了更好的理解傅里叶分解,我们引入空间频率的概念,空间频率表示特定波形在单位间距内重复的次数,也表示透镜和照相底片的分辨率。
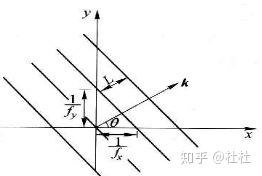
沿等位相线法线方向,存在:
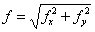
得到结论:逆傅里叶变换的物理意义是:物函数
2、基本定理
我们在初步认识了傅里叶变换的原理后,下面来总结梳理一下重要的定理:
(1)线性定理:
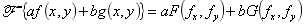
该线性定理反应了波的叠加原理,常令
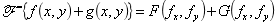
(2)缩放定理:
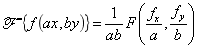
进而可以推出反演定理(对称性定理):
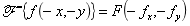
(3)位移定理:
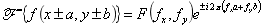
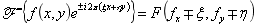
(4)帕塞瓦尔定理:
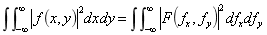
(5)广义帕色瓦尔定理:
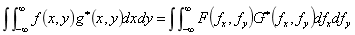
这里要注意的是:
(6)卷积定理:
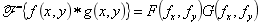
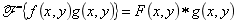
(7)互相关定理:
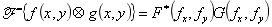
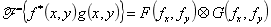
(8)自相关定理:
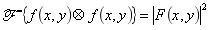
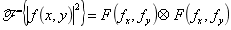
即信号的自相关函数与其功率谱函数之间存在傅里叶变换关系。
(9)积分定理:
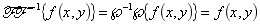
(10)迭代变换定理:
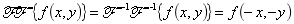
该定理得到了镜像。
(11)微分变换定理:
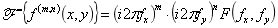
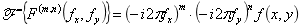
(12)积分变换定理:
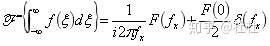
(13)共轭变换定理:
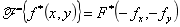
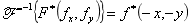
推论:若
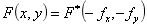
具有上述特性的函数我们称为厄米特函数。
3、常用的的傅里叶变换
左边是原函数,后面是频谱函数,如下:
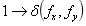
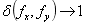
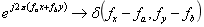
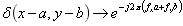
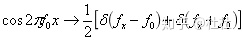
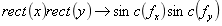
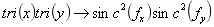
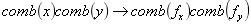
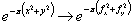
最后
以上就是完美白猫最近收集整理的关于三角波的傅里叶变换公式_傅里叶变换那点事儿的全部内容,更多相关三角波内容请搜索靠谱客的其他文章。








发表评论 取消回复