FIR滤波器设计

一、 窗口设计法（时域）

1.   以一个截止频率为 ωc的线性相位理想低通滤波器为例,讨论FIR的设计问题。

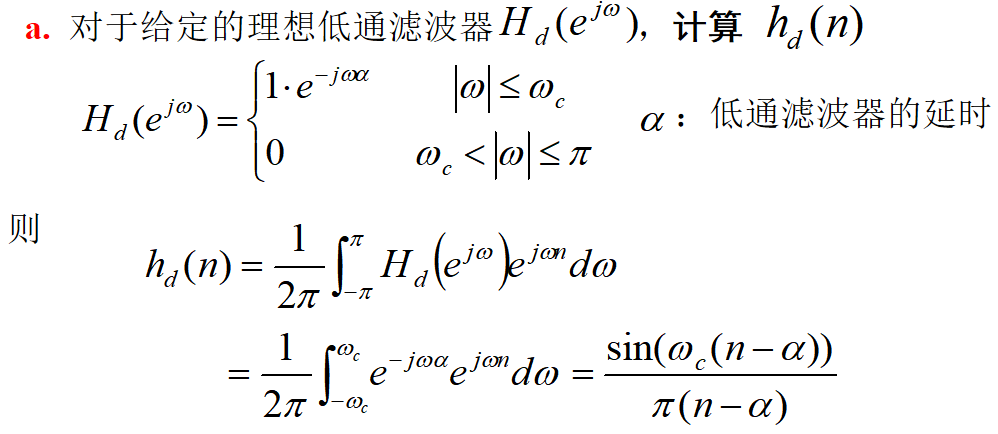
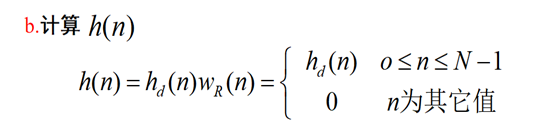
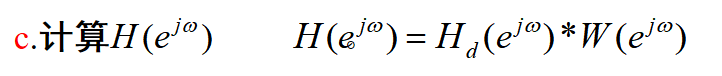
.2  几种常用的窗函数

      1). 矩形窗，

     2). 汉宁窗（升余弦窗）

     3.) 汉明窗（改进的升余弦窗）

     4). 布莱克曼窗（二阶升余弦窗）

5) .凯塞窗

在窗口函数方面，MATLAB可计算以下的窗口函数：

     W=hanning(N)

     W=hamming(N)

     W=blackman(N)

     W=kaiser(N, beta)

变量Ｎ是窗函数的长度，beta就是凯塞窗的参数β，它可以利用以上讨论的公式计算，Ｗ是返回的窗口函数，长度为Ｎ。

［M, Wc, beta, ftype］=kaiserord(f, a, dev, fs)

f为通带和阻带边界频率，最高为fs/2；a为相应频带的幅度值；dev为波动值；fs缺省为2。M是滤波器阶数；Wc边界频率；beta即β；ftype是滤波器类型，低通为low。

例子1 用凯塞窗设计一FIR低通滤波器，低通边界频率，阻带边界频率，阻带衰减不小于50dB。

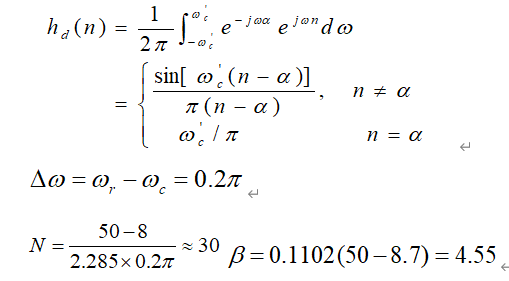
 wn=kaiser(30,4.55);

  nn=[0:1:29];

  alfa=(30-1)/2;

  hd=sin(0.4*pi*(nn-alfa))./(pi*(nn-alfa));

  h=hd.*wn';

  [h1,w1]=freqz(h,1);

  plot(w1/pi,20*log10(abs(h1)));

  axis([0,1,-80,10]);

  grid;

  xlabel('归一化频率/p')

  ylabel('幅度/dB')

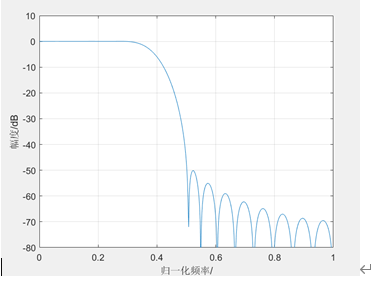
fir1是用窗函数法设计线性相位FIR DF的工具箱函数，以实现线性相位FIR DF的标准窗函数法设计。

b=fir1(n,wn);

b=fir1(n,wn,'ftype');

b=fir1(n,wn,'ftype',window);

b为滤波器系数，n为滤波器阶数，Wn—截止频率，0≤Wn≤1

ftype—当指定ftype时，可设计高通和带阻滤波器。   

Ftype=high时，设计高通FIR滤波器；

ftype=stop时设计带阻FIR滤波器。低通和带通

FIR滤波器无需输入ftype参数。

Window—窗函数。窗函数的长度应等于FIR滤波器系数个数，即阶数n+1

b=fir1(n,wn);

b=fir1(n,wn,'ftype');

b=fir1(n,wn,'ftype',window);

b为滤波器系数，n为滤波器阶数，Wn—截止频率，0≤Wn≤1

ftype—当指定ftype时，可设计高通和带阻滤波器。

例子2 用窗函数法设计一线性相位高通滤波器。该滤波器在通带和阻带具有相同的波动幅度0.01，通带范围为0.35pi~pi，阻带范围为0~0.2pi

采用fir1的函数，凯塞窗，MATLAB程序如下：

    f=[0.2 0.35];    a=[0 1];

    dev=[0.01 0.01];

    [M, Wc, beta, ftype]=kaiserord(f, a, dev);

    h=fir1(M, Wc,ftype, kaiser(M+1,beta));

   [h1,w1]=freqz(h,1);

    plot(w1/pi,20*log10(abs(h1)));

    axis([0,1,-80,10]);  grid;

    xlabel('归一化频率/pi'), ylabel('幅度/dB')

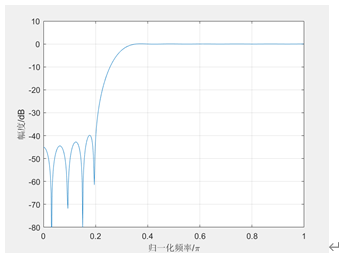
例子3 试用Kaiser窗设计满足下列指标的具有2个通带FIR滤波器

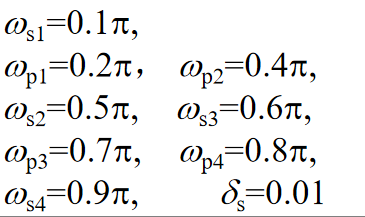
f=[0.1 0.2 0.4 0.5 0.6 0.7 0.8 0.9];

a=[0,1,0,1,0];Rs=0.01;

dev=Rs*ones(1,length(a));

[N,Wc,beta,ftype] = kaiserord(f,a,dev);

h = fir1(N,Wc,ftype,kaiser(N+1,beta));
         [h1,w1]=freqz(h,1);

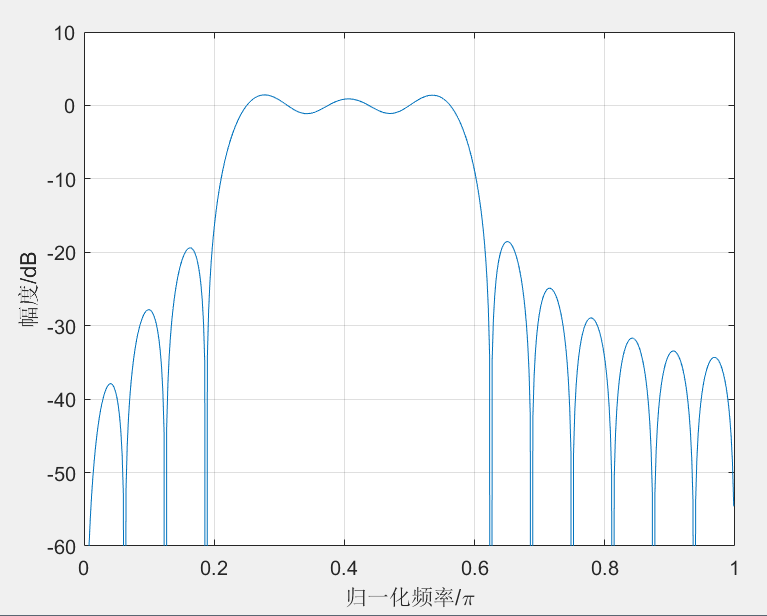
  plot(w1/pi,20*log10(abs(h1)));

xlabel('Normalized frequency');

ylabel('Gain, db');grid;

axis([0 1 -80 5]);

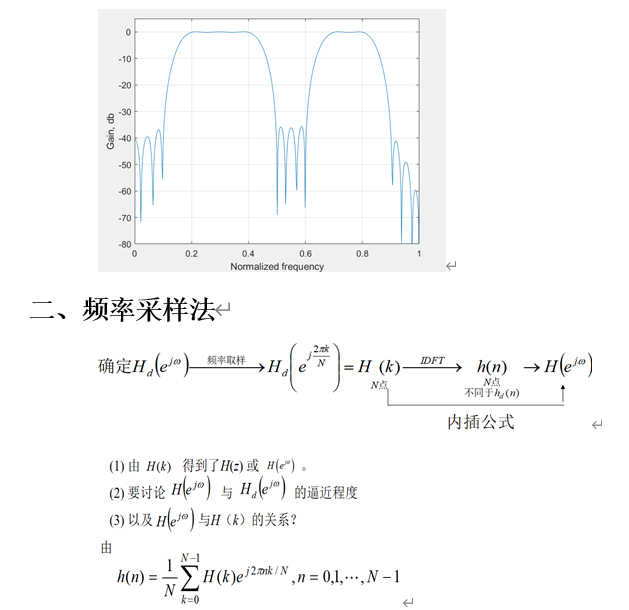
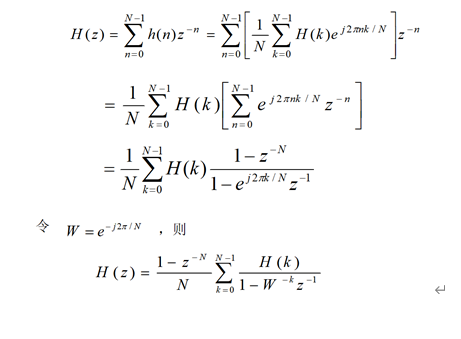
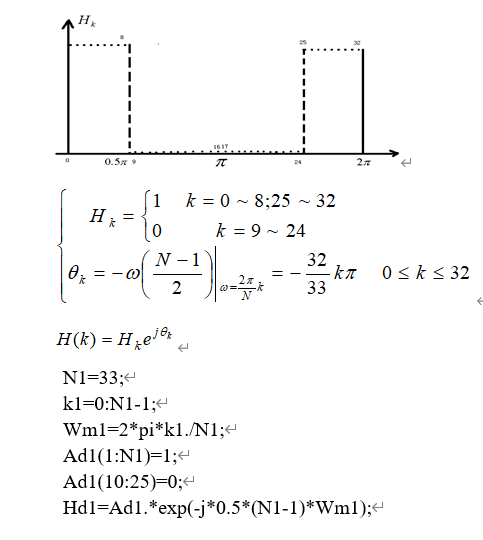
h1=real(ifft(Hd1));

w1=linspace(0,pi-0.1,1000);

H1=freqz(h1,[1],w1);

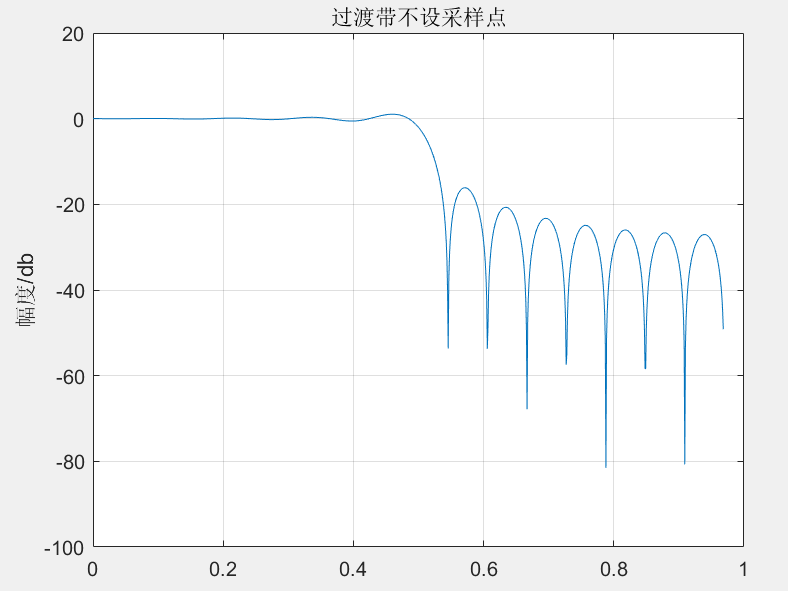
plot(w1/pi,20*log10(abs(H1)));grid;

axis([0 1 -100 20]);

xlabel('pi');

ylabel('幅度/db');

title('过渡带不设采样点');

最后

以上就是大意金针菇为你收集整理的FIR滤波器设计的全部内容，希望文章能够帮你解决FIR滤波器设计所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。