FFT变换频谱图中幅值的设置方法

按照上篇博文所画出来的频谱图中，原信号的每个频率是准确地找出来了，但是各个频率点所对应的的幅值可不是原信号中真正的幅值，因为在进行DFT(FFT)变换的时候，已经把幅值改变了，要想让频谱图的纵坐标显示为原信号中真正的幅值其实也很简单，代码如下：

clear all
fs=150;%采样频率要大于等于原信号中最高频率的二倍
N=150;
t=(0:N-1)/fs;
y=0.5*sin(2*pi*65*t)+0.8*cos(2*pi*40*t)+0.7*cos(2*pi*30*t);
F=fft(y,N);
freq=(0:N/2)*fs/N;%只画(0,fs/2)范围内的频率分量，起始坐标是0，因为只有(0,fs/2)范围内的频率才有意义，因为原信号的最大频率小于等于fs
F1=abs(F(1:N/2+1));%频谱图中各频率点对应的幅值并不是原信号中真正的幅值
F2=abs(F(1:N/2+1))*2/N;%频谱图中各频率点对应的的幅值就是原信号中真正的幅值
subplot(211)
stem(freq,F1,'k');%依据频率坐标来绘制傅里叶变换后的信号的频率-幅度谱，注意F的起始坐标是1
xlabel('频率(Hz)');
ylabel('幅值');
xlim([0 130]);
subplot(212)
stem(freq,F2,'k');
xlabel('频率(Hz)');
ylabel('幅值');
xlim([0 130]);

运行结果：

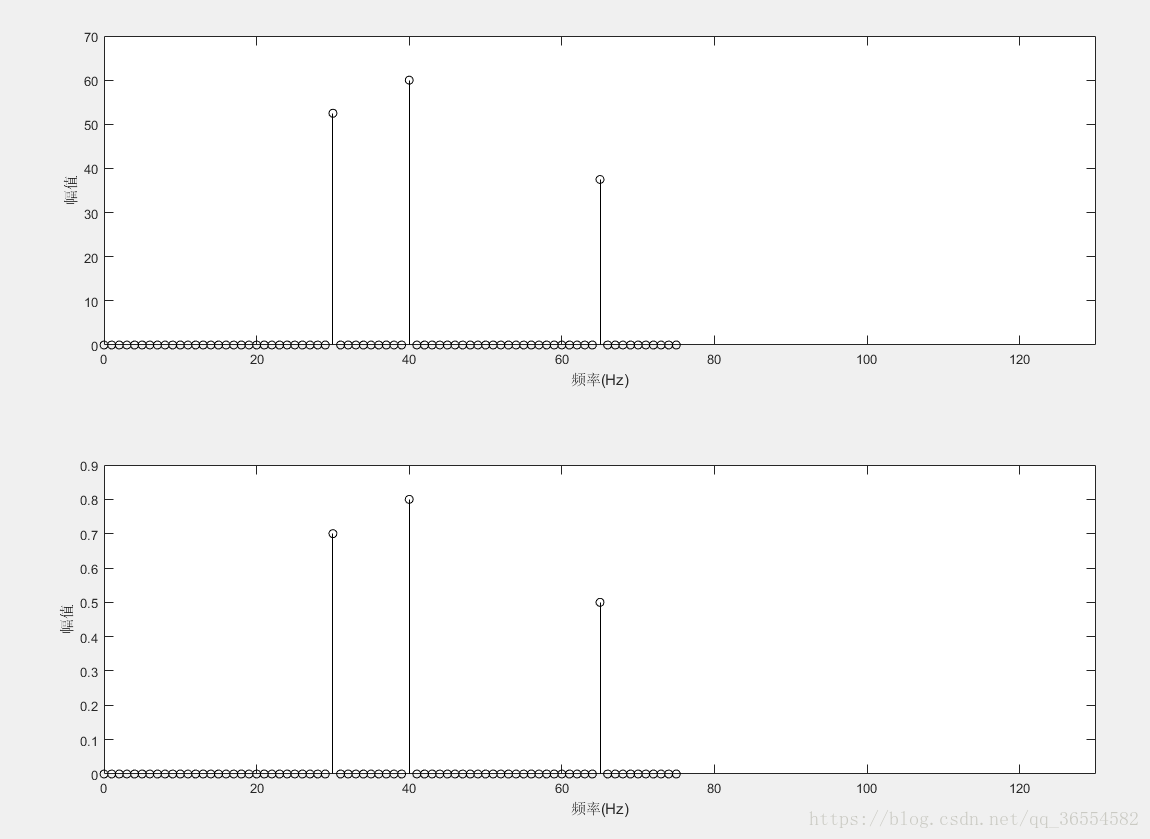
我们只需要把之前的语句F1=abs(F(1:N/2+1));
更改为：F2=abs(F(1:N/2+1))*2/N; 即可，也就是说FFT变换后的各频率点对应的幅度和原信号真正的幅度就相差了一个2/N或者说是N/2的关系。

接下来再看一个例子：

clear all
fs=15000;%采样频率要大于等于原信号中最高频率的二倍
N=15000;
t=(0:N-1)/fs;
y=0.5*sin(2*pi*1000*t)+0.8*cos(2*pi*3000*t)+0.7*cos(2*pi*6000*t);
F=fft(y,N);
freq=(0:N/2)*fs/N;%只画(0,fs/2)范围内的频率分量，起始坐标是0，因为只有(0,fs/2)范围内的频率才有意义，因为原信号的最大频率小于等于fs
F1=abs(F(1:N/2+1));%频谱图中各频率点对应的幅值并不是原信号中真正的幅值
F2=abs(F(1:N/2+1))*2/N;%频谱图中各频率点对应的的幅值就是原信号中真正的幅值
subplot(211)
plot(freq,F1,'k');%依据频率坐标来绘制傅里叶变换后的信号的频率-幅度谱，注意F的起始坐标是1
xlabel('频率(Hz)');
ylabel('幅值');
xlim([0 8000]);
subplot(212)
plot(freq,F2,'k');
xlabel('频率(Hz)');
ylabel('幅值');
xlim([0 8000]);
ylim([0 1]);

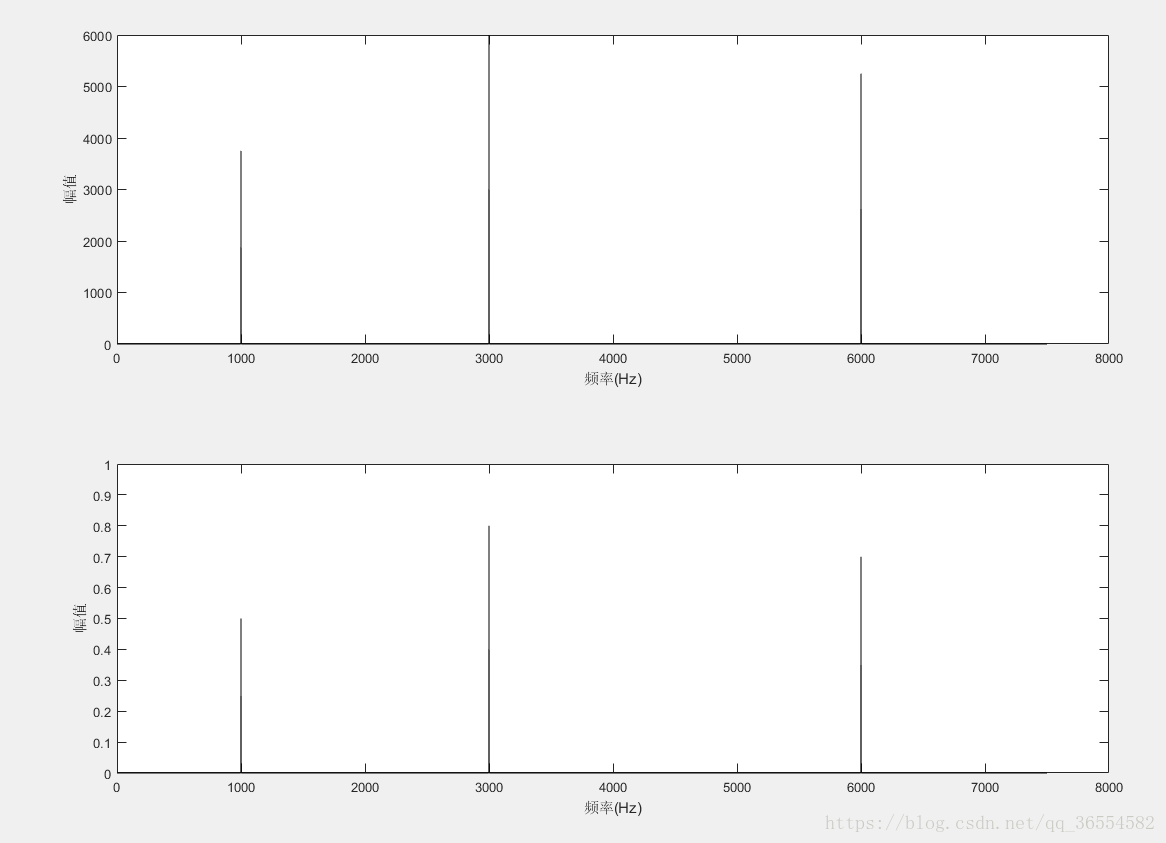
最后

以上就是深情板凳为你收集整理的FFT变换频谱图中幅值的设置方法的全部内容，希望文章能够帮你解决FFT变换频谱图中幅值的设置方法所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。