1 GLU
GLU的起源是2016年由Yann N. Dauphin在
论文:Language Modeling with Gated Convolutional Networks
在语言模型的建模方法上相比于循环神经网络更具有竞争力,提出了一种简单的线性门控单元来堆叠卷积层从而使得文本中的token可以并行化处理来获得上下文的语义特征。
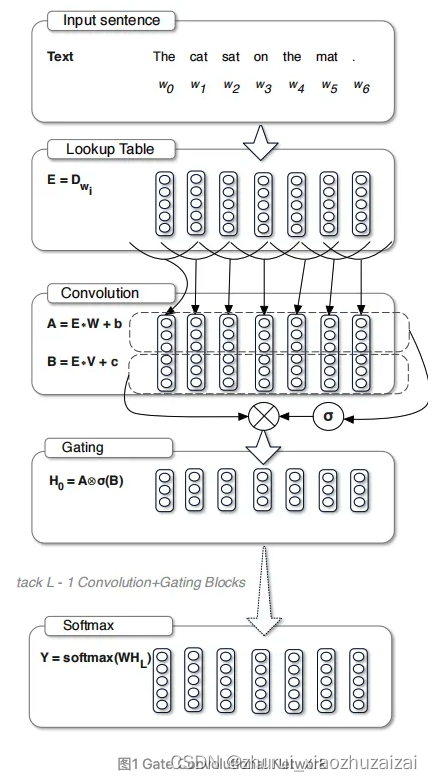
而且与循环神经网络相比,其复杂度从O(N)降低到O(N/k),其中的k为卷积核的宽度,N为文本的上下文集合。这里的循环神经网络不单指RNN,还有其变种LSTM、GRU等等。论文中整个模型的结构如下图所示:输入层(Input Sentence+Lookup Table)、中间层(Convolution+Gate)以及输出层(Softmax)
输入层(Input Sentence+Lookup Table)
W=[w1,w2,……,wn],wn代表输入token,通过lookuptable得到embedding
E=[ew1,ew2,……,ewn]
中间层(Convolution+Gate)
首先输入到两个卷积层Conv1和Conv2 ,得到两个输出Ccon1和Ccon2,然后将Ccon2利用sigmoid函数进行激活得到h(Ccon2),然后通过Hadamard积逐位相乘得到相应的隐层向量h,更一般的可表示为:
X表示输入的向量,N表示输入文本中token的集合长度,m表示向量的维度,k表示卷积核的宽度,n表示输出的特征图大小(输出维度),V,W是可训练的参数矩阵,b,c表示对应的偏置项。
可以看出,门控线性单元与LSTM的门控本质上是一样的,只不过在计算隐层向量时不需要依赖上一个时间步。通过堆叠多层卷积就可以得到文本的上下文信息GTU的门控机制,其实也就是将GLU的前一项利用 函数进行激活,但引入一个激活函数就代表梯度在反向传播过程中就多了一项衰减项,因此,作者认为GLU优于GTU。GTU表示为:
对于采用sigmoid可能导致的梯度弥散问题,作者还在网络加入了残差。并且由于sigmoid在中间部分(近0端)表现近似于线性,所以整个模型的复杂度基本近似于线性。
输出层(Softmax),
由于在语言模型建模过程中的词表V是相当大的,也就是在进行一次预测时会撸一遍词表,其复杂度就为O(V),会严重影响模型的效率。所以作者采用了AdaptiveSoftmax作为归一化函数,将词表中的词分为高频词和低频词两组,将不同词频区间的词分为不同的clusters,按照词频高的cluster优先访问的原则,对cluster中的每个词进行softmax来预测,所以也要求词表需要按照频率从大到小进行排列。以此来加快模型训练时的效率。
门控线性单元(Gated Linear Unit, GLU),它是门控增强的改进版 MLP 变体。
GLU 已被证实在很多情况下都有效,并在 SOTA Transformer 中使用;
GLU Variants Improve Transformer标准FFN
GLU
一般情况下的GLU是U不加激活函数而V加Sigmoid
GAU
论文《Transformer Quality in Linear Time》
其核心思路是将注意力和 GLU 作为一个统一层,并尽可能多地共享它们的计算,具体如下图所示。这样做不仅实现了更高的参数和计算效率,而且自然地赋能一个强大的注意力门控机制。
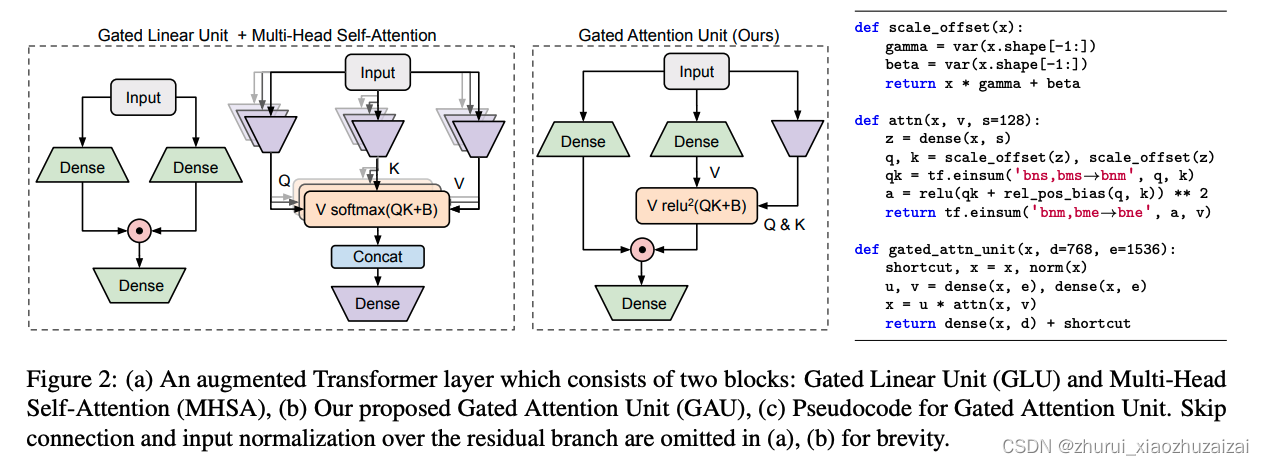
结合GLU。将Attention和GLU结合
在式(3)中,如果A等于单位阵I,那么它就是GLU式的FFN;而如果A是全1矩阵,那么它就是普通的注意力机制。所以说,(3)是Attention和FFN的一个简单而自然的融合,我们期望它能同时替换掉Attention和FFN,甚至有更好的表现。
Z是共享表示 (s<<d), 论文中s =128
当GAU只有一个头时,Wz的参数量就很少了,主要参数量在Wu,Wv,Wo上,所以GAU的参数量大约为3de;
而在标准的Transformer中,Attention的参数量为4d2,FFN的参数量为8d2(标准FFN中一般是e=4d),所以总参数量为12d2。
因此,从参数量看,当e=2d时,两层GAU大致上就等于原来的Attention+FFN。
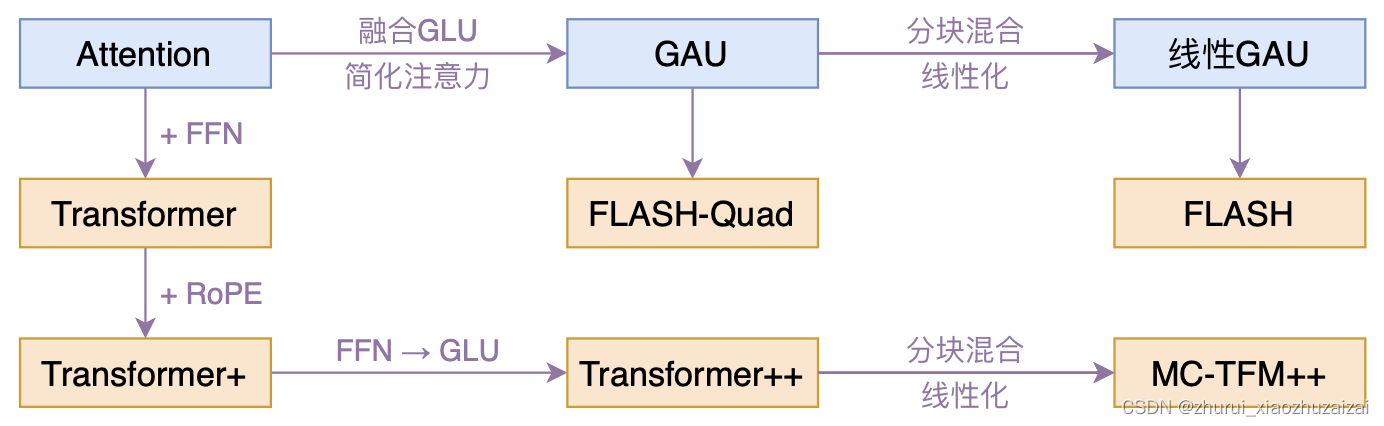
“n层Attention+n层FFN”的标准Transformer模型,对应的就是“2n层GAU”的新模型,我们记为FLASH-Quad,其中Quad是“Quadratic”的简写,表明复杂度依然是二次的。
降低复杂度的方法
(1)将注意力计算稀疏化、即人为根据先验知识规定哪些token可以进行注意力计算(典型代表: Longformer、BigBird等)
(2)将注意力计算线性化。提出另外的方法,去逼近标准注意力的效果(典型代表: Linformer、Performer等),如下公式所示:
假设Q , K , V 的维度都为:( m , d )
右边是正常计算:m∗d∗m + m∗d∗m = 2dm2,跟序列长度m成平方正比.
左边:先计算KTV, d∗m∗d+d∗m∗d,即:2md2.第二种方法随着序列的边长,效率会远高于第一种方法
分块注意力的计算
假设序列长度为n,每个块的维度为c,则可分成n/c个块(默认可整除)。
块内注意力:
每个块的token内部自行交互,本质上也算是“稀疏化”的一种,其复杂度大致是????(n/c×c2)=????(nc),正比于n。实现时相当于头数为n/c、序列长度为c的多头注意力,可以充分地并行,
而如果想要做Decoder,那么mask掉注意力矩阵的上三角部分即可
全局注意力:
注意,这个操作跟直接用完整矩阵Qlin,Klin∈ℝn×s与V做线性Attention是完全等价的,写成这样只是更好地体现跟分块的联系。
如果是做Decoder,那么要防止泄漏未来信息,所以要改为cumsum形式:
这种情况下,为了保持并行性,我们只需要b(n/c)se的空间复杂度,而如果不分块直接用线性Attention,那么是bns2(要是原始的用法还要加上多头,那就是bhns2),在当前参数设置下有e/c≪s,所以是更省显存了。
最终GAU:基于线性版本GAU搭建的Transformer模型
GAU与标准的多头注意力之间MHSA的比较,其实也就是FLASH-Quad和标准Transformer的比较了,如下图:
注意横轴是速度,纵轴是效果,这种图越靠近右上角的点意味着越理想(速度和效果都最优),
所以上图显示不管哪种规格的模型,GAU都比相应的多头注意力模型更有优势。
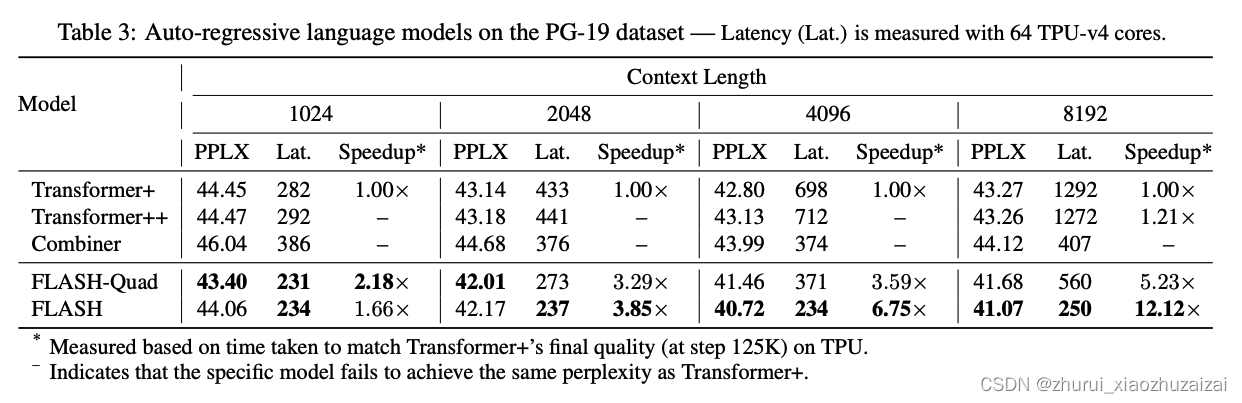
FLASH模型的实验表格
1、尽管FLASH-Quad和Transformer都是二次复杂度,但FLASH-Quad效果更好、速度更快;
2、在序列足较长时,线性复杂度的FLASH比FLASH-Quad更快,并且效果相仿。
与 Transformer 层相比,每个 GAU 层更便宜。更重要的是,它的质量更少依赖于注意力精度。事实上,小单头、无 softmax 注意力的 GAU 与 Transformers 性能相近。
最后
以上就是多情店员最近收集整理的关于FFN -> GLU -> GAU1 GLUGAU的全部内容,更多相关FFN内容请搜索靠谱客的其他文章。
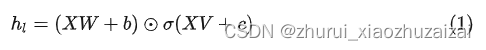
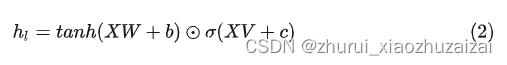
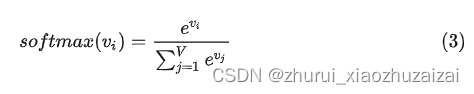

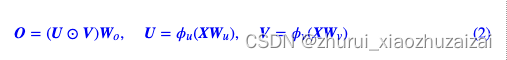


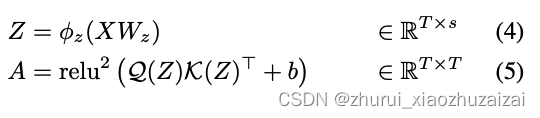
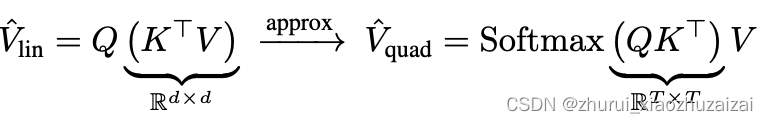

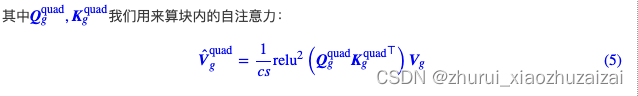

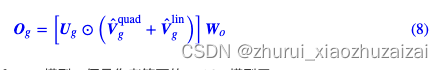









发表评论 取消回复