Matlab常用数学功能速览

106 阅读 0 评论 70 点赞

我是靠谱客的博主喜悦未来，最近开发中收集的这篇文章主要介绍Matlab常用数学功能速览，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

1.语法

行向量：
x=[1,2.2,3,4,5.5,6]
可以等效于一维数组

列向量：
y=[1,-2,3,4.12,5.5,6]'
'（英文单引号）表示向量或者矩阵的转置

矩阵：
a=[1,2,3 ; 4,5,6]
a'表示a的转置

矩阵乘/除法和元素乘除法
若a,b均为矩阵，则a*b表示矩阵a乘矩阵b，a，b必须符合矩阵乘法的条件。
a.*b表示a中每个元素乘以b中对应元素得到的矩阵，此时a,b必须行列数都相等

 >>a=[1,2;3,4];
 >>b=[3,5;7,9];
 >> a*b

ans =

    17    23
    37    51

>> a.*b

ans =

     3    10
    21    36

所以[1,2;3,4]*[1,2]'可以执行，结果为

而[1,2;3,4].*[1,2]'则会报错

Error using  .* 
Matrix dimensions must agree.

匿名函数
fun = @(x) (sin(x^2)./x)
@(x)表示自变量是x，后面函数表达式两端的括号可以去掉，不影响使用,个人习惯用括号来包裹

二元：
fun = @(x,y)(y*sin(x)+x*cos(y));
依此类推

2.函数

ode23
求解非刚性微分方程的低阶方法
[t,y] = ode23(odefun,tspan,y0)
odefun为微分方程，tspan指定微分区间，y0为初始条件，对应的是tspan中的第一个元素的函数值，请看下面的例子：
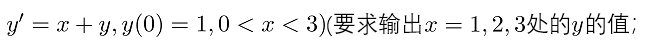
在这里插入图片描述

>> fun=@(x,y)x+y;
>> [x,y]=ode23(fun,[0,1,2,3],1)
x =
     0
     1
     2
     3


y =
    1.0000
    3.4341
   11.7625
   36.1040

integral
数值积分
q = integral(fun,xmin,xmax) 使用全局自适应积分和默认误差容限在 xmin 至 xmax 间以数值形式为函数 fun 求积分。

quadl(fun,a,b)
求函数fun在(a,b)上的的积分,误差小于 10^-6
范围 a 和 b 必须是有限的

例：

f= @(x)(x.*log(x.^4).*asin(1./x.^2));
quadl(f,1,3)

ans =
    2.4598

dblquad(fun,xmin,xmax,ymin,ymax)
矩形区域上的二重积分的数值计算
例：
F = @(x,y)(y*sin(x)+x*cos(y));
dblquad(F,pi,2*pi,0,pi)

ans =

   -9.8696

quad2d(fun,a,b,c,d)
计算二重数值积分
逼近 fun(x,y) 在平面区域 a≤x≤b 和 c(x)≤y≤d(x) 上的积分。边界 c 和 d 均可为标量或函数句柄
例如：求解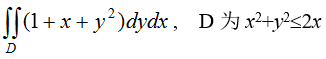在这里插入图片描述
fun=@(x,y)1+x+y.^2;
clo=@(x)-sqrt(2*x-x.^2);
dup=@(x)sqrt(2*x-x.^2);
quad2d(fun,0,2,clo,dup)


ans =

    7.0686

trapz(x,y)
梯形数值积分,根据 X 指定的坐标或标量间距对 Y 进行积分。
如果只有一个参数:
trapz(y), 则是采用单位间距计算 Y 的近似积分

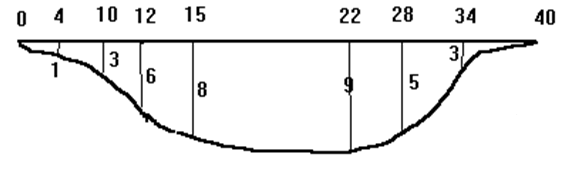
比如下面图形的面积就可以用以下语句求出
x=[0 4 10 12 15 22 28 34 40];
y=[0 1 3 6 8 9 5 3 0];
trapz(x,y)

在这里插入图片描述

diff(x)
计算沿大小不等于 1 的第一个数组维度的 X 相邻元素之间的差分，
如果 X 是长度为 m 的向量，则 Y = diff(X) 返回长度为 m-1 的向量。Y 的元素是 X 相邻元素之间的差分。
Y = [X(2)-X(1) X(3)-X(2) ... X(m)-X(m-1)]

例：
>>diff([1,2,4,5,7,8,10])

ans =
     1     2     1     2     1     2

其中第一个等于2-1, 第二个数等于4-2, 第三个数等于5-4，第四个数等于7-5，以此类推
如果 X 是不为空的非向量 p×m 矩阵，则 Y = diff(X) 返回大小为 (p-1)×m 的矩阵，其元素是 X 的行之间的差分。
Y = [X(2,:)-X(1,:); X(3,:)-X(2,:); ... X(p,:)-X(p-1,:)]
例：
diff([1,2,3,4;5,6,7,8;9,10,11,12])