算法与数据结构---红黑树

77 阅读 0 评论 51 点赞

我是靠谱客的博主高高树叶，最近开发中收集的这篇文章主要介绍算法与数据结构---红黑树，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

算法与数据结构—红黑树

1. 前言
红黑树是一个平衡的二叉树，但不是一个完美的平衡二叉树。虽然我们希望一个所有查找都能在lgN次比较内结束，但是这样在动态插入中保持树的完美平衡代价太高，所以，我们稍微放宽一下限制，希望找到一个能在对数时间内完成查找的数据结构，这样就产生了红黑树。要了解红黑树就必须先了解二叉树。红黑树是在普通二叉树上，对没个节点添加一个颜色属性形成的。
2. 树
2.1. 树的定义
树是一种数据结构，它是由n（n>=1）个有限节点组成一个具有层次关系的集合。如下图所示：
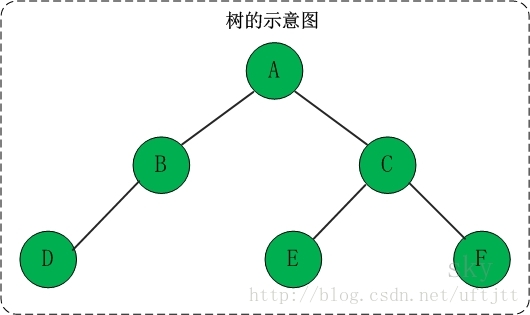
这里写图片描述
把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。它具有以下的特点：
(1) 每个节点有零个或多个子节点；
(2) 没有父节点的节点称为根节点；
(3) 每一个非根节点有且只有一个父节点；
(4) 除了根节点外，每个子节点可以分为多个不相交的子树。
2.2. 树的基本术语
若一个结点有子树，那么该结点称为子树根的”双亲”，子树的根是该结点的”孩子”。有相同双亲的结点互为”兄弟”。一个结点的所有子树上的任何结点都是该结点的后裔。从根结点到某个结点的路径上的所有结点都是该结点的祖先。
结点的度：结点拥有的子树的数目。
叶子：度为零的结点。
分支结点：度不为零的结点。
树的度：树中结点的最大的度。
层次：根结点的层次为1，其余结点的层次等于该结点的双亲结点的层次加1。
树的高度：树中结点的最大层次。
无序树：如果树中结点的各子树之间的次序是不重要的，可以交换位置。
有序树：如果树中结点的各子树之间的次序是重要的, 不可以交换位置。
森林：0个或多个不相交的树组成。对森林加上一个根，森林即成为树；删去根，树即成为森林。
3. 二叉树
3.1. 二叉树的定义
二叉树是每个节点最多有两个子树的树结构。它有五种基本形态：二叉树可以是空集；根可以有空的左子树或右子树；或者左、右子树皆为空。
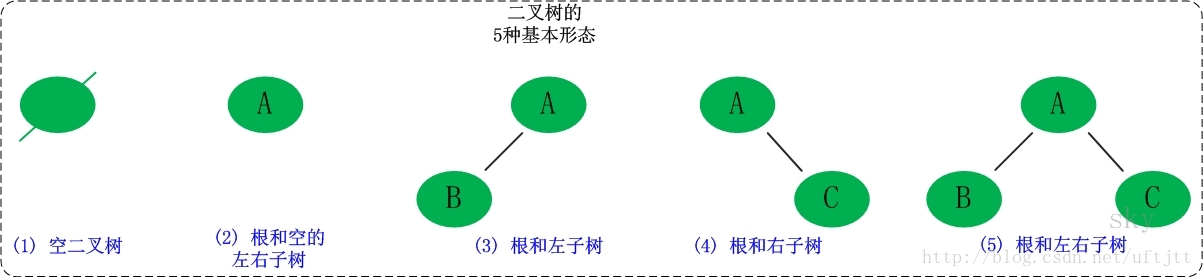
这里写图片描述
3.2. 二叉树的性质
二叉树有以下几个性质：TODO(上标和下标)
性质1：二叉树第i层上的结点数目最多为

2 i - 1 (i \geq 1)

$2^{i-1} (i≥1)$ 。
性质2：深度为k的二叉树至多有

2 k - 1 (k \geq 1)

$2^k-1(k≥1)$ 个结点。
性质3：包含n个结点的二叉树的高度至少为

l o g 2 (n + 1)

$log2 (n+1)$ 。
性质4：在任意一棵二叉树中，若终端结点的个数为n0，度为2的结点数为n2，则n0=n2+1。
3.2.1 性质1：二叉树第i层上的结点数目最多为 $2 i - 1 (i \geq 1)$ $2^{i-1} (i≥1)$
证明：下面用”数学归纳法”进行证明。
(1) 当i=1时，第i层的节点数目为

2 i - 1 = 20 = 1

$2^{i-1}=2^{0}=1$ 。因为第1层上只有一个根结点，所以命题成立。
(2) 假设当i>1，第i层的节点数目为

2 i - 1

$2^{i-1}$ 。这个是根据(1)推断出来的！
下面根据这个假设，推断出”第(i+1)层的节点数目为

2 i

$2^{i}$ ”即可。
由于二叉树的每个结点至多有两个孩子，故”第(i+1)层上的结点数目” 最多是 “第i层的结点数目的2倍”。即，

第 (i + 1) 层 上 的 结 点 数 目 最 大 值 = 2 \times 2 i - 1 = 2 i

$第(i+1)层上的结点数目最大值=2×2^{i-1}=2^{i}$ 。
故假设成立，原命题得证！
3.2.2 性质2：深度为k的二叉树至多有 $2 k - 1 (k \geq 1) 个结点$ $2^{k}-1(k≥1)个结点$
证明：在具有相同深度的二叉树中，当每一层都含有最大结点数时，其树中结点数最多。利用”性质1”可知，深度为k的二叉树的结点数至多为：

20 + 21 + \dots + 2 k - 1 = 2 k - 1

$2^0+2^1+…+2^{k-1}=2^k-1$
故原命题得证！
3.2.3 性质3：包含n个结点的二叉树的高度至少为 $l o g 2 (n + 1)$ $log2 (n+1)$
证明：根据”性质2”可知，高度为h的二叉树最多有

2 h - 1

$2^{h}–1$ 个结点。反之，对于包含n个节点的二叉树的高度至少为

l o g 2 (n + 1)

$log2(n+1)$ 。
3.2.4 性质4：在任意一棵二叉树中，若终端结点的个数为n0，度为2的结点数为n2，则n0=n2+1
证明：因为二叉树中所有结点的度数均不大于2，所以结点总数(记为n)=”0度结点数(n0)” + “1度结点数(n1)” + “2度结点数(n2)”。由此，得到等式一。
(等式一) n=n0+n1+n2
　另一方面，0度结点没有孩子，1度结点有一个孩子，2度结点有两个孩子，故二叉树中孩子结点总数是：n1+2n2。此外，只有根不是任何结点的孩子。故二叉树中的结点总数又可表示为等式二。
(等式二) n=n1+2n2+1
由(等式一)和(等式二)计算得到：n0=n2+1。原命题得证！
4. 满二叉树、完全二叉树和二叉查找树
4.1 满二叉树
定义：

高 度 为 h ， 并 且 由 2 h - 1 个 结 点 的 二 叉 树 ， 被 称 为 满 二 叉 树 。

$高度为h，并且由2^{h} –1个结点的二叉树，被称为满二叉树。$
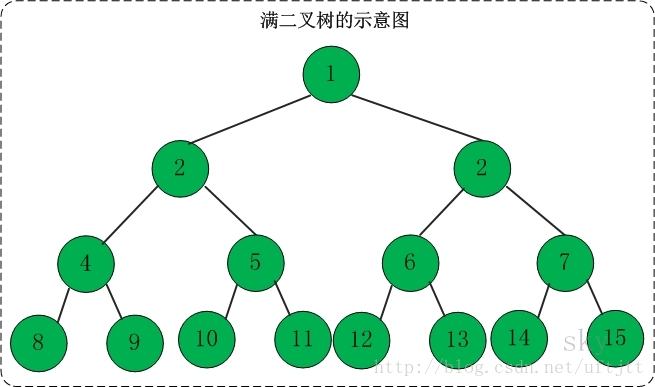
这里写图片描述

4.2 完全二叉树
定义：一棵二叉树中，只有最下面两层结点的度可以小于2，并且最下一层的叶结点集中在靠左的若干位置上。这样的二叉树称为完全二叉树。
特点：叶子结点只能出现在最下层和次下层，且最下层的叶子结点集中在树的左部。显然，一棵满二叉树必定是一棵完全二叉树，而完全二叉树未必是满二叉树。
4.3 二叉查找树
定义：二叉查找树(Binary Search Tree)，又被称为二叉搜索树。设x为二叉查找树中的一个结点，x节点包含关键字key，节点x的key值记为key[x]。如果y是x的左子树中的一个结点，则key[y] <= key[x]；如果y是x的右子树的一个结点，则key[y] >= key[x]。
在二叉查找树中：
(1) 若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
(2) 任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
(3) 任意节点的左、右子树也分别为二叉查找树。
(4) 没有键值相等的节点（no duplicate nodes）。
5. 2-3-4 Tree(2-3-4树)
二叉查找树（Binary Search Tree，简称BST）是一棵二叉树，它的左子节点的值比父节点的值要小，右节点的值要比父节点的值大。它的高度决定了它的查找效率。
我们知道二叉查找树。每个节点只可以有一个key，而2-3-4树就是将节点的key的数量增加，可以有多个key，并且2-3-4树可以保持完美平衡（Perfect balance. Every path from root to leaf has same length）
什么是完美平衡（Perfect balance）？实际上就是每条从根节点到叶节点的路径的高度都是一样的（Every path from root to leaf has same length）
2-3-4树的名字是根据子节点数来确定的。
我们看2-3-4树的key的种类。

    2-node: one key, two children.一个key值，两个儿子节点
    3-node: two keys, three children。两个key值，三个儿子节点
    4-node: three keys, four children.三个key值，四个儿子节点

其中2-node的左孩子就代表比key小，右孩子就代表比key大，
3-node的左孩子代表比第一个key小，中间的孩子代表值位于第一个key和第二个key之间，右孩子代表值大于第二个key
4-node同理
接下来我们看一棵2-3-4树的例子，如图下图所示：
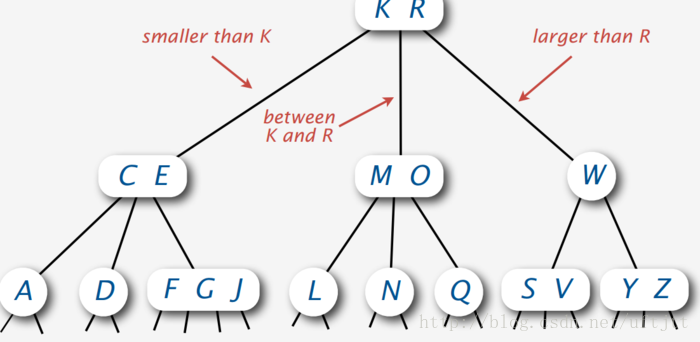
这里写图片描述
5.1 2-3-4树的查找（Search in a 2-3-4 Tree）
2-3-4的查找类似于BST的查找，只要递归找到所在的子树就可以。

    比较要查找的key与当前节点中的key值
    根据key值选择要查找的key所存在的子树区间
    重复上述步骤（递归实现），直到查找到key

5.2 2-3-4的插入（Insertion in a 2-3-4 Tree）
2-3-4的插入有几种情况，下面我们会一一的讨论。
首先，如果是向一个2-node插入节点的话，那么直接将它转换为3-node就可以了。如下图所示：
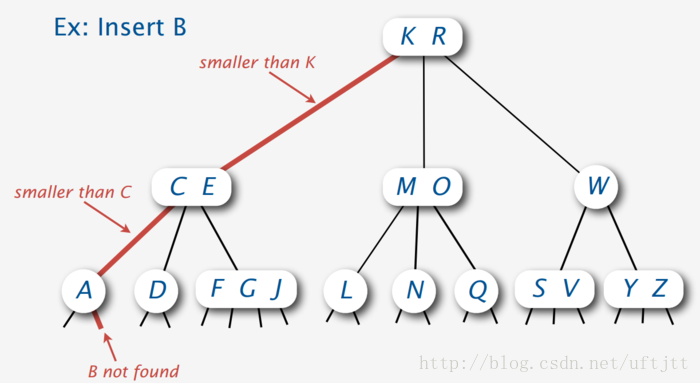
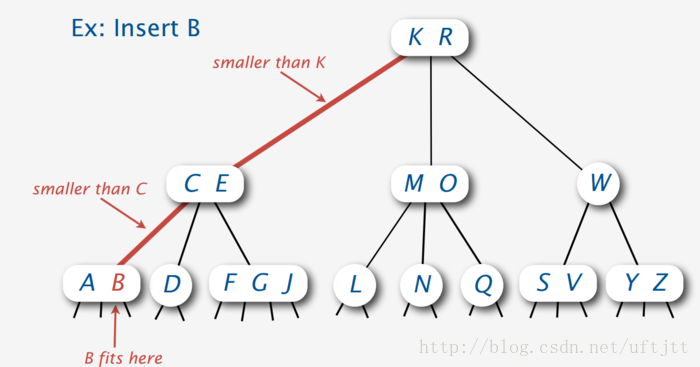
这里写图片描述

如果我们是向3-node插入，就将3-node变成4-node即可，如下图：

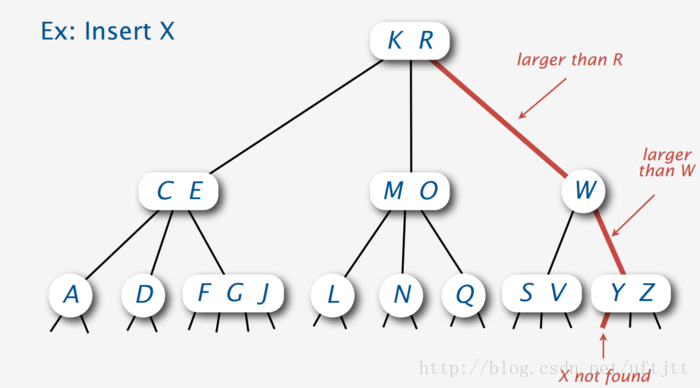
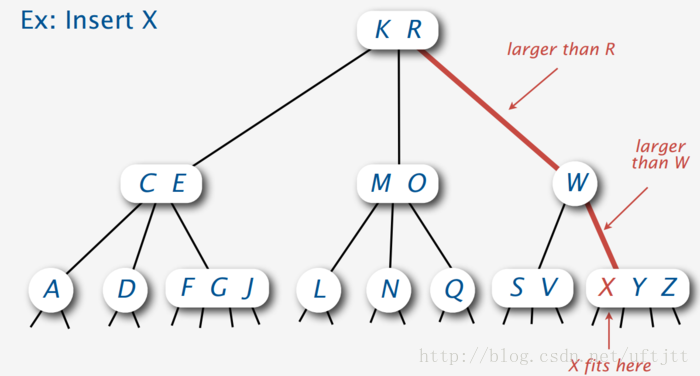
那么问题就来了，如果我们向4-node插入呢?
显然我们无法直接插入，因为4-node已经是最大的节点了。
这时，我们就需要对节点进行一些变换
最常用的方法就是将4-node的中间节点向上移动，移动到父节点中。这样就可以插入了。
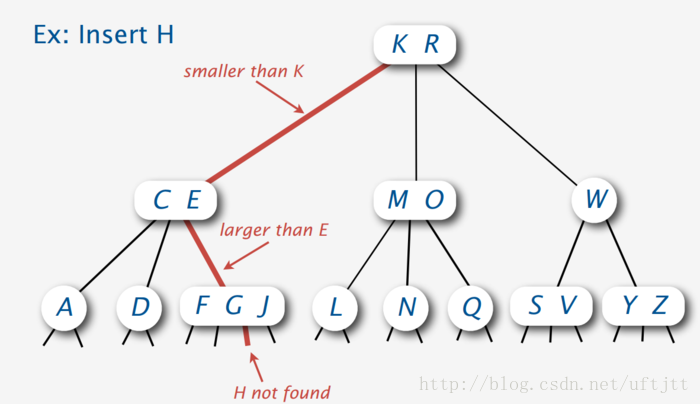
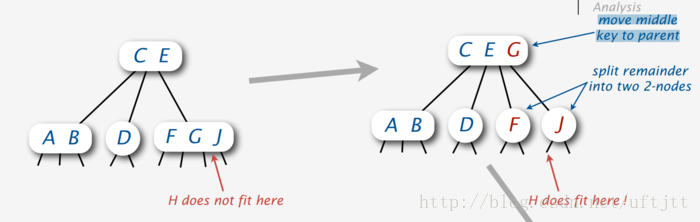
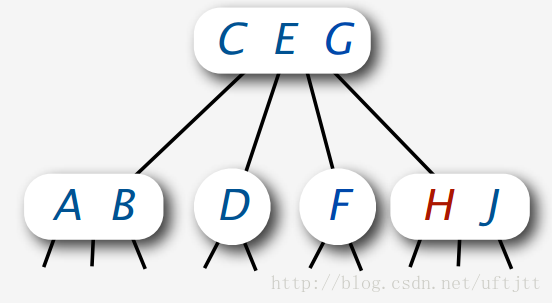
这里写图片描述

但这个方法有一个问题，就是如果父节点是4-node，那么就无法切分中间节点了。
一种解决的方法就是ensures that the “current” node is not a 4-node ，我们做出保证父节点永远不会是4-node，就是说4-node不会出现在最后一层以外的层上。
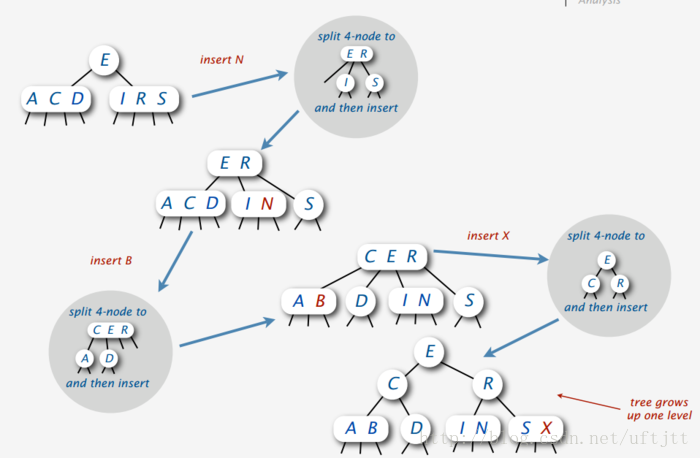
这里写图片描述
最终我们会发现，2-3-4树所有叶子节点都在同一个高度上。如下图：

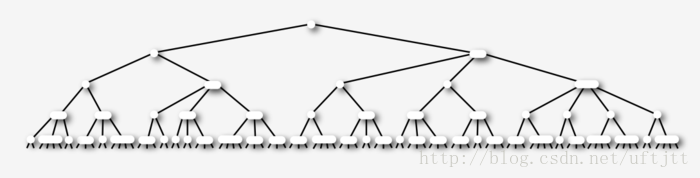
我们分析2-3-4树的效率：
2-3-4的高度的最坏情况（全是2-node），也就相当于演变成了平衡二叉树：相当于平衡二叉树 lgN
2-3-4树高度的最好情况（全是4-node），log4 N = 1/2 lg N（但我们知道这种情况是不可能出现的，因为我们要求4-node的父节点或者子节点不能是4-node）
对于100万个节点，2-3-4树的高度会在10~20之间
对于10亿的节点，2-3-4树的高度会在15~30之间
由此来看，2-3-4树的效率比平衡二叉树要好，但是问题在于，2-3-4树并不好实现
首先，我们需要用三种不同类型的节点代表2-3-4node
然后，在插入节点的时候，我们可能需要进行大量的切分4-node的工作
我们可能也需要频繁的在三种节点之间进行转换
6. 红黑树
红黑树是在普通二叉树上，对没个节点添加一个颜色属性形成的，同时整个红黑二叉树需要同时满足一下五条性质，红黑树需要满足的五条性质：
性质一：节点是红色或者是黑色；
在树里面的节点不是红色的就是黑色的，没有其他颜色，要不怎么叫红黑树呢，是吧。
性质二：根节点是黑色；
根节点总是黑色的。它不能为红。
性质三：每个叶节点（NIL或空节点）是黑色；
这个可能有点理解困难，可以看图：
这里写图片描述
这个图片就是一个红黑树，NIL节点是个空节点，并且是黑色的。
性质四：每个红色节点的两个子节点都是黑色的（也就是说不存在两个连续的红色节点）；
就是连续的两个节点不能是连续的红色，连续的两个节点的意思就是父节点与子节点不能是连续的红色。
性质五：从任一节点到其每个叶节点的所有路径都包含相同数目的黑色节点；
还是看图：
这里写图片描述
从根节点到每一个NIL节点的路径中，都包含了相同数量的黑色节点。
这五条性质约束了红黑树，可以通过数学证明来证明，满足这五条性质的二叉树可以将查找删除维持在对数时间内。
当我们进行插入或者删除操作时所作的一切操作都是为了调整树使之符合这五条性质。
下面我们先介绍两个基本操作，旋转。
旋转的目的是将节点多的一支出让节点给另一个节点少的一支，旋转操作在插入和删除操作中经常会用到。
6.1 左旋
看图：
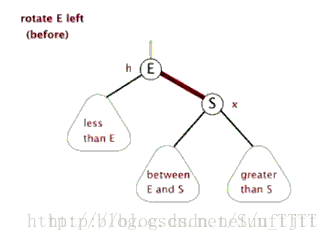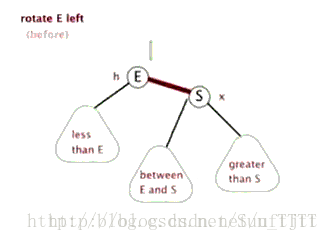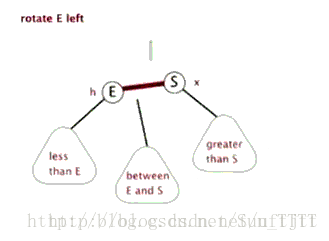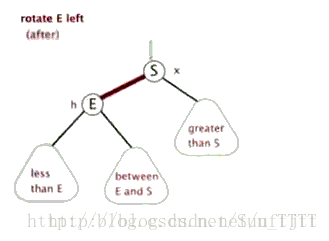
这里写图片描述
6.2 右旋
看图：

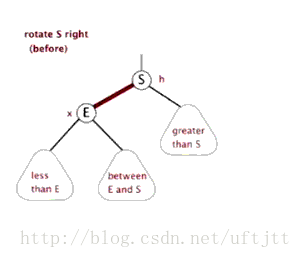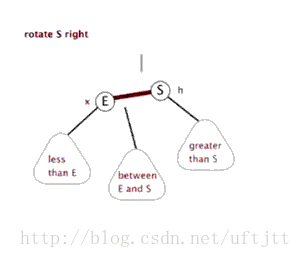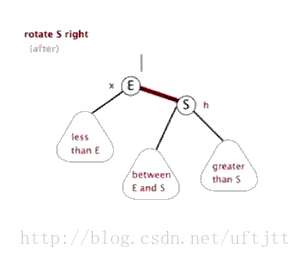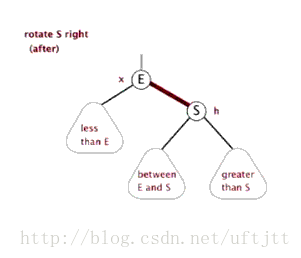
6.3 插入结点
在介绍插入结点前先明确下各个结点的叫法，如下图：

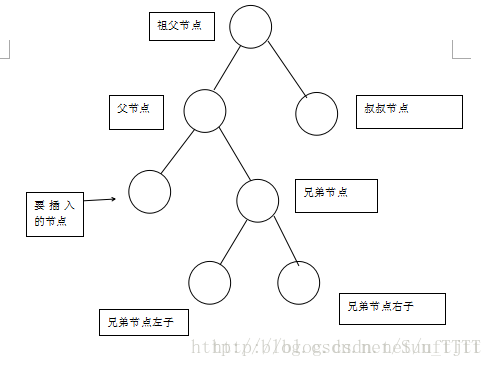
因为要满足红黑树的这五条性质，如果我们插入的是黑色节点，那就违反了性质五，需要进行大规模调整，如果我们插入的是红色节点，那就只有在要插入节点的父节点也是红色的时候违反性质四或者是当插入的节点是根节点时，违反性质二，所以，我们把要插入的节点的颜色变成红色。
下面是可能遇到的插入的几种状况：
（1）当插入的节点是根节点时，直接涂黑即可；
（2）当要插入的节点的父节点是黑色的时候。如下图：
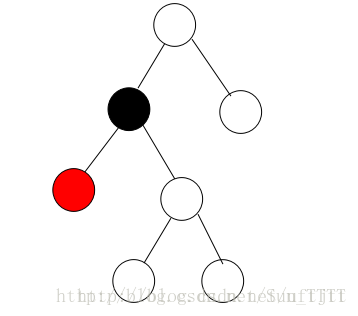
这里写图片描述
这个时候插入一个红色的节点并没有对这五个性质产生破坏。所以直接插入不用在进行调整操作。
（3）如果要插入的节点的父节点是红色且父节点是祖父节点的左支的时候。
这个要分两种情况，一种是叔叔节点为黑的情况，一种是叔叔节点为红的情况。
当叔叔为黑时，也分为两种情况，一种是要插入的节点是父节点的左支，另一种是要插入的节点是父亲的右支。
我们先看一下当要插入的节点是父节点的左支的情况：
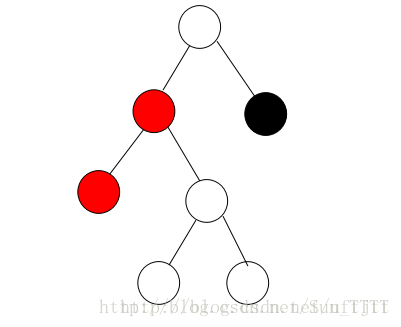
这里写图片描述
这个时候违反了性质四，我们就需要进行调整操作，使之符合性质四，我们可以通过对祖父节点进行右旋同时将祖父节点和父节点的颜色进行互换，这样就变成了：

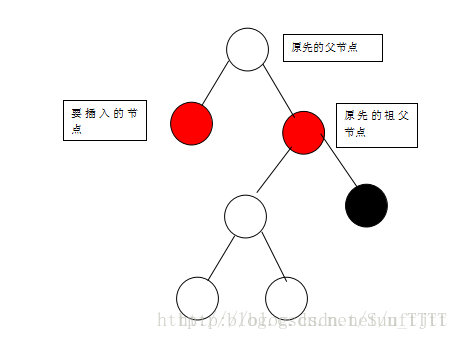
经过这样的调整可以符合性质四并且不对其他性质产生破坏。
当插入的节点是父节点的右支的时候，如下图：
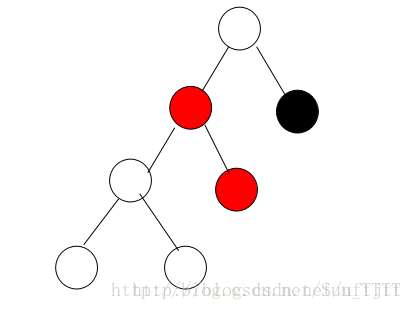
这里写图片描述
当要插入的节点是父节点的右支的时候，我们可以先对父节点进行左旋，变成如下：

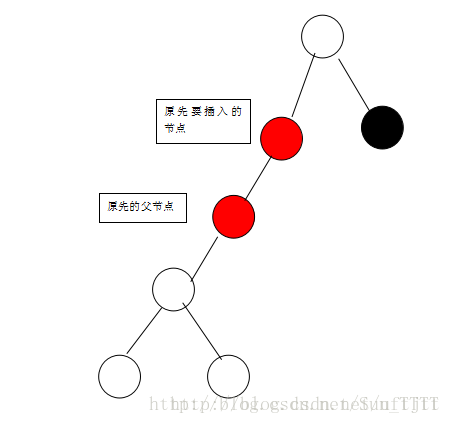
如果我们把原先的父节点看做是新的要插入的节点，把原先要插入的节点看做是新的父节点，那就变成了当要插入的节点在父节点的左支的情况，对，是的，就是按照当要插入的节点在父节点的左支的情况进行旋转，旋转完之后变成如下：
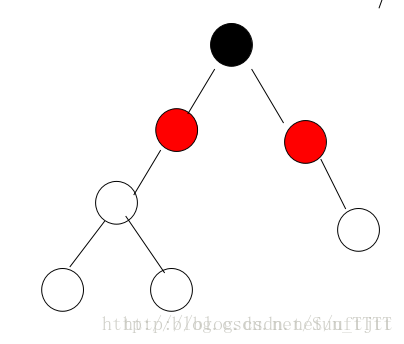
这里写图片描述
（4）如果要插入的节点的父节点是红色且父节点是祖父节点的右支的时候；
这个时候的情况跟情况3所表述的情况是一个镜像，将情况3的左和右互换一下就可以了。
（5）如果要插入的节点的父节点是红色并且叔叔节点也为红色，如下：
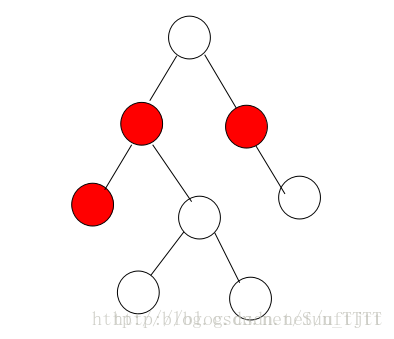
这里写图片描述
这个时候，只需将父亲节点和叔叔节点涂黑，将祖父节点涂红。
以上就是插入的全部过程。
6.4 删除操作
首先你要了解普通二叉树的删除操作：
1.如果删除的是叶节点，可以直接删除；
2.如果被删除的元素有一个子节点，可以将子节点直接移到被删除元素的位置；
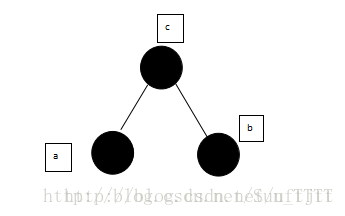
3.如果有两个子节点，这时候就可以把被删除元素的右支的最小节点（被删除元素右支的最左边的节点）和被删除元素互换，我们把被删除元素右支的最左边的节点称之为后继节点（后继元素），然后在根据情况1或者情况2进行操作。如图：
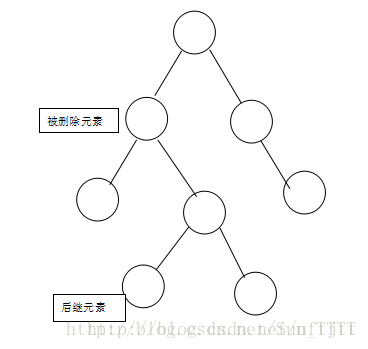
这里写图片描述
将被删除元素与其右支的最小元素互换，变成如下图所示：

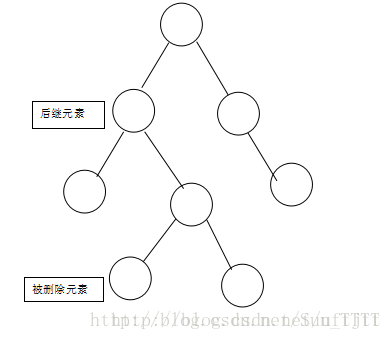
然后再将被删除元素删除：

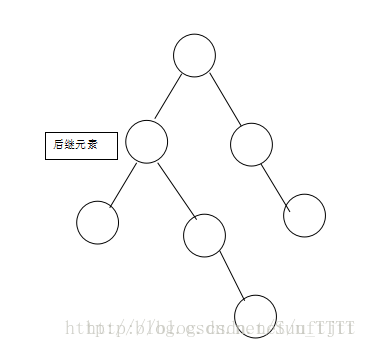
我们下面所称的被删除元素，皆是指已经互换之后的被删除元素。
加入颜色之后，被删除元素和后继元素互换只是值得互换，并不互换颜色，这个要注意。
6.5 红黑树删除规则
下面开始讲一下红黑树删除的规则：
（1）当被删除元素为红时，对五条性质没有什么影响，直接删除。
（2）当被删除元素为黑且为根节点时，直接删除。
（3）当被删除元素为黑，且有一个右子节点为红时，将右子节点涂黑放到被删除元素的位置，如图：
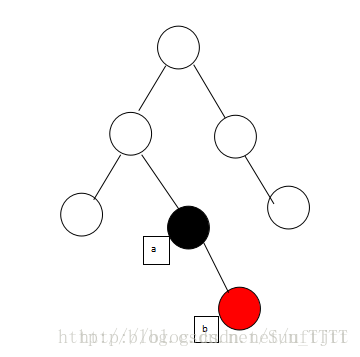
这里写图片描述
删除后变为：

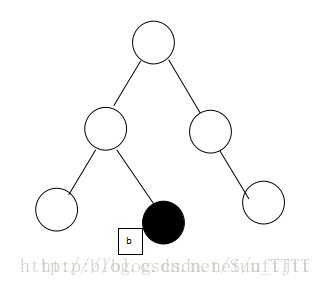
（4）当被删除元素为黑，且兄弟节点为黑，兄弟节点两个孩子也为黑，父节点为红，此时，交换兄弟节点与父节点的颜色；NIL元素是指每个叶节点都有两个空的，颜色为黑的NIL元素，需要他的时候就可以把它看成两个黑元素，不需要的时候可以忽视他。
如图：
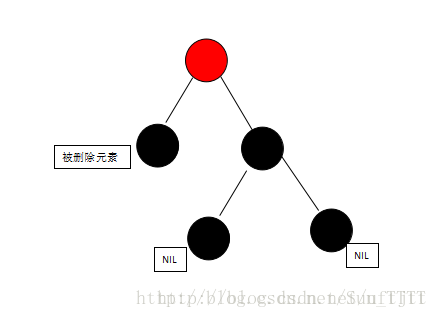
这里写图片描述
删除后变为：

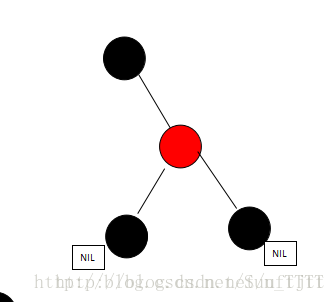
（5）当被删除元素为黑、并且为父节点的左支，且兄弟颜色为黑，兄弟的右支为红色，这个时候需要交换兄弟与父亲的颜色，并把父亲涂黑、兄弟的右支涂黑，并以父节点为中心左转。如图：
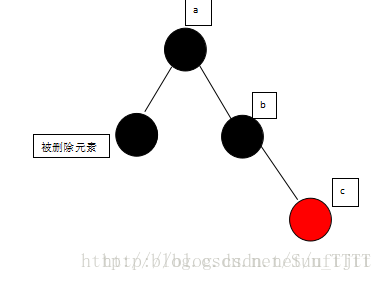
这里写图片描述
删除后变为：

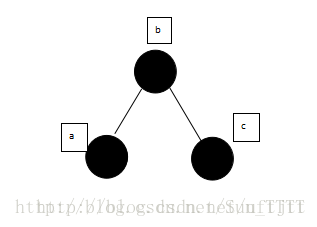
（6）当被删除元素为黑、并且为父节点的左支，且兄弟颜色为黑，兄弟的左支为红色，这个时候需要先把兄弟与兄弟的左子节点颜色互换，进行右转，然后就变成了规则5一样了，在按照规则5进行旋转。如图：
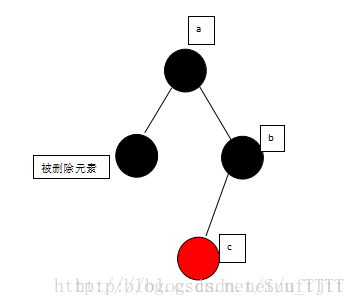
这里写图片描述
先兄弟与兄弟的左子节点颜色互换，进行右转，变成：

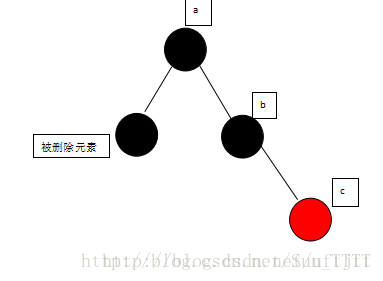
然后在按照规则5进行旋转，变成：

（7）当被删除元素为黑且为父元素的右支时，跟情况5.情况6 互为镜像。
（8）被删除元素为黑且兄弟节点为黑，兄弟节点的孩子为黑，父亲为黑，这个时候需要将兄弟节点变为红，再把父亲看做那个被删除的元素（只是看做，实际上不删除），看看父亲符和哪一条删除规则，进行处理变化如图，
由：
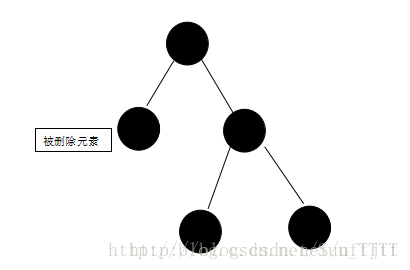
这里写图片描述
删除后变为：

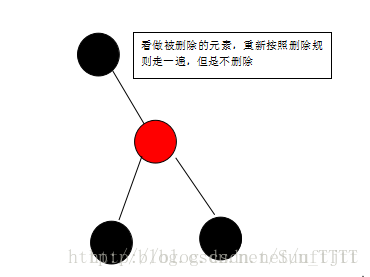
（9）当被删除的元素为黑，且为父元素的左支，兄弟节点为红色的时候，需要交换兄弟节点与父亲结点的颜色，以父亲结点进行左旋，就变成了情况4，在按照情况四进行操作即可，变化如下，由：
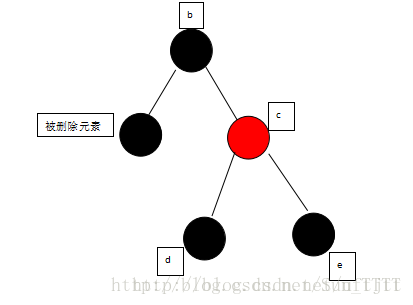
这里写图片描述
交换兄弟节点与父亲结点的颜色，以父亲结点进行左旋变成：

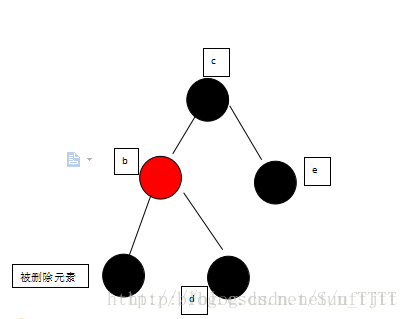
在按照情况四进行操作，变成：

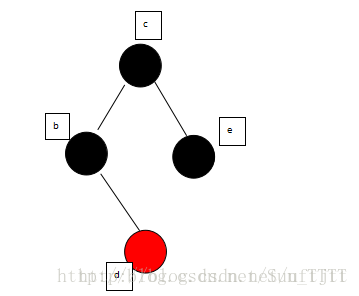
7. 总结
在添加删除的时候，时刻要记得更改根元素的颜色为黑。
这里并没有语言实现，只是讲了一下红黑树的插入删除步骤，你可以根据步骤自己把红黑树实现。
最后：
1.红黑树的实现其实是一个2、3、4树，只是将双节点或者三节点用红色进行了标示，如果你将红色节点放到和它父元素相同的高度，并把它和父元素看做是一个元素，你就会发现，变成了一个高度为lgN的二叉树，这个2.3.4树对红黑树很有启发意义。
2.上面的步骤其实可以不用死记硬背，是可以推导出来的，因为我们是把一个平衡但通过插入或者删除破坏了平衡的红黑树再次平衡，同过旋转让位，改变红黑颜色，使之符合那五条基本性质。比如遇到删除操作情况四的时候，我们可以把那个删除元素去除，发现左边比右边少一个黑元素，这个时候，怎么办，我们发现兄弟节点的子元素有一个红元素，操作这个不会影响那五条性质，所以我们通过变换颜色，旋转，即可让左右两边的的黑色数目一样。
3.旋转操作的目的是出让一个元素到另外的地方并且符合二叉树左小右大的性质，交换颜色的目的是为了保持红黑树的那五条性质。
4.要时刻记得，一切的操作都是为了保持那五条性质。