MATLAB--simulink工具箱的使用（2）

MATLAB–simulink工具箱的使用（2）

实例：计算机控制系统–倒立摆实验

之前在（1）中已经讲过了simulink工具箱的基本操作，今天就用simulink工具箱对倒立摆进行仿真控制。

1. 倒立摆系统
   这里我们用到的是直线一级倒立摆系统，在忽略空气阻力和摩擦的影响之后可以简化为以下模型。
   
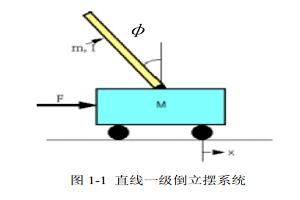
   在建立系统模型的状态空间表达式的过程中，我们考虑到有以下的物理量：
   倒立摆系统中，我们需要控制的量有φ（摆杆与垂直向上方向的夹角），ω（摆杆与垂直向上方向的角速度，即φ的导数），x（小车的位置），ν（小车的速度，即x的导数）。则在建立状态空间表达式的时候，选择这四个物理量为状态变量。经过推导，可以得到模型的状态空间表达式为：
   
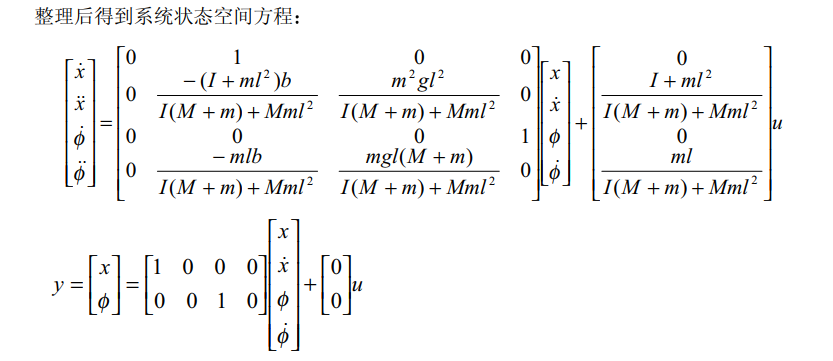
2. 倒立摆系统连续控制器的设计
   （1）仿真原系统的输出响应
   由上，我们已经得到了倒立摆系统的状态空间表达式。在simulink中对此开环系统进行仿真。
   实际系统参数如下：
   
   假定以后研究的对象是φ（摆杆与垂直向上方向的夹角），那么以阶跃信号作为输入信号进行开环系统的仿真，可以发现输出响应如下，由此得出不稳定。
   

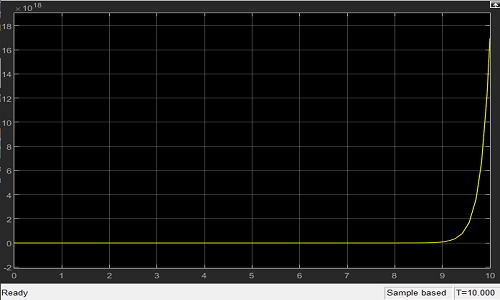
（2）设计准备
确定设计要求：对倒立摆系统中的角度状态进行控制
①调节时间ts<3；②阻尼比>0.7；③单位阶跃干扰下最大偏离<5°。
在matlab中用tf函数将状态空间表达式转化为传递函数，得到角度与输入的传递函数为：

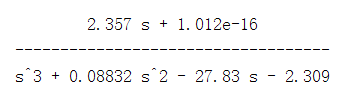
（3）在sisotool工具箱中进行控制器设计
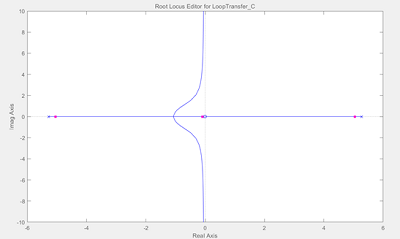
①首先，通过根轨迹图可以看到被控对象是不稳定的。根轨迹图中始终有极点处在s平面的右半平面（无论如何选择k值都有闭环极点在s右半平面）

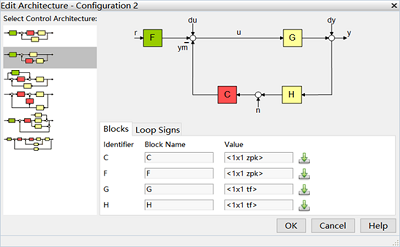
②选择合适的系统模型，选择控制器在反馈通道上的模式。（C就是控制器）

③确定控制器的零极点。观察可以发现，根轨迹图之所以在右半平面恒有值，是因为在原点有一个零点。

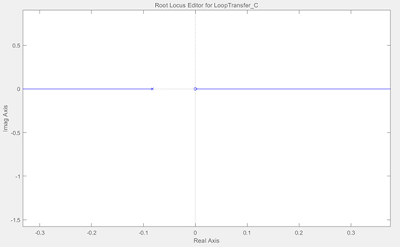
所以控制器先添加一个积分器，让整个系统在原点的零点进行零极相消。再给控制器添加两个零点-2和-4（随机选择），让根轨迹往左拉。最后再添加一个极点-50，使得影响尽量小。最后系统的根轨迹图如下所示，可以发现当选择k为一定范围内的值时，可以保证所有此时所有的闭环极点都在s的左半平面。
加入零极点之后的系统根轨迹图形为：

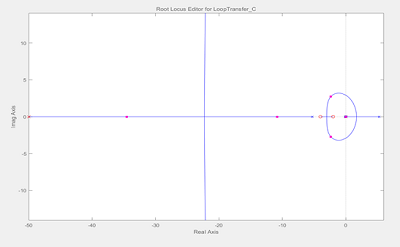
④确定控制器的k值。
由于设计的系统指标要求为，调节时间ts<3；阻尼比>0.7；单位阶跃干扰下最大偏离<5°，也就是单位阶跃响应图中的最大偏离<0.08rad。将设计指标在根轨迹图中显示出来（只能显示调节时间和阻尼比的要求）。需要主导极点的位置在图中白色部分。
体现调节时间要求的方法是:根轨迹图上右键->Design requirements->new->Settling time->选择小于3s。（阻尼比要求也一样，最后选择Damping ratio，大于0.7）

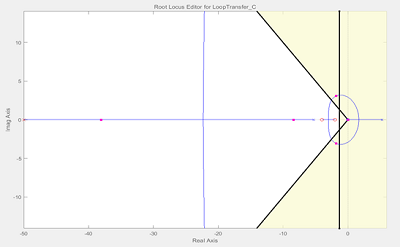
调节k值，当k=400时，发现主导极点在上图中的白色部分（即满足调节时间和阻尼比的要求），且单位阶跃响应图中最大偏移量不超过0.08rad。

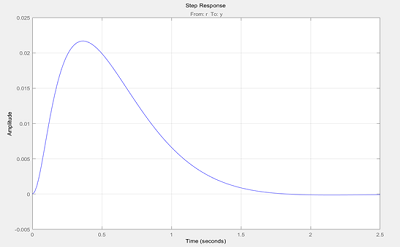
（4）得出结果并仿真
所以最终得到的控制器的传递函数为[400(s+2)(s+4)]/[s(s+50)]。
在simulink中仿真，可以看出最终输出趋于稳定，且满足设计要求。

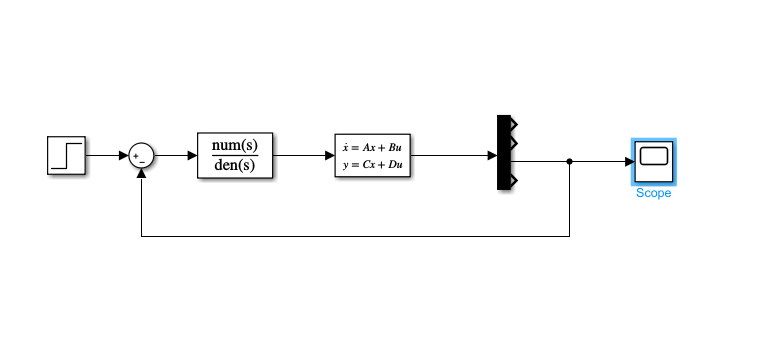
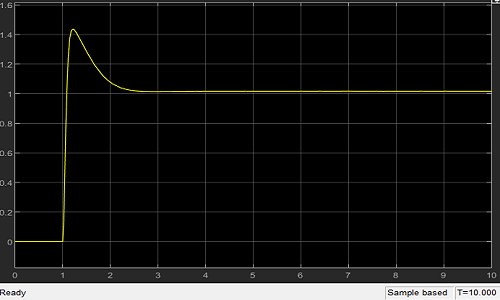
由此，就设计好了倒立摆系统的角度控制器！
成功！！撒花！！！！

最后

以上就是爱听歌小兔子为你收集整理的MATLAB--simulink工具箱的使用（2）的全部内容，希望文章能够帮你解决MATLAB--simulink工具箱的使用（2）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。