原创文章，转载请注明出处：
http://blog.csdn.net/chengcheng1394/article/details/78756522
请安装TensorFlow1.0，Python3.5，seaborn
项目地址：
https://github.com/chengstone/LotteryPredict

前言

使用人工智能技术来预测彩票，是这次的主题，那么预测哪种彩票呢？我们先选择简单一些的，就是排列组合少一些的，如果证明我们的模型work，再扩展到其他的彩票上。最终我选择了排列三, 从000-999的数字中选取1个3位数，一共有1000种，中奖概率就是千分之一，够简单了吧。
历史数据在这里。
数据是按照每期一组数的顺序排列的，从第一期到最新的一期，实际上是时间序列的数据。跟回归预测有很大的区别，因为特征上没有特殊的意义，不具备一组特征x映射到label y的条件。但是按照时间序列来训练的话就不一样了，输入x是一期的开奖结果，要学习的y是下一期的开奖结果。

LSTM介绍

我们需要从过往的历史数据中寻找规律，LSTM再适合不过了。如果你对LSTM不熟悉的话，以下几篇文章建议你阅读：
Understanding LSTM Networks
[译] 理解 LSTM 网络
RNN以及LSTM的介绍和公式梳理

看看数据集的结构

数据情况：
不重复单词(彩票开奖记录)的个数: 988
开奖期数: 4656期
行数: 4657
平均每行单词数: 1.0

开奖记录从 0 到 10:
202
243
580
306
598
900
761
262
891
623

一共4656条记录，4600多期了。共出现了988个不重复的结果，就是说还有（1000 – 988）12组数到现在还没有开出来过。文件中第一行是最新的一期，第二行是之前的一期，。。。，最后一行是第一期。
我们可以把三个数组合成一组数，就像数据集中体现的那样，并且把一组数当作一个数或者说当作一个单词。这样在预处理数据集的时候会简单一些，从索引到单词（0 -> ‘000’）和从单词到索引（‘012’-> 12）其实都是同一个数。

预测网络介绍

网络的输入是每一期的开奖结果，总共有1000组数，用one hot编码是一个1000维的稀疏向量：

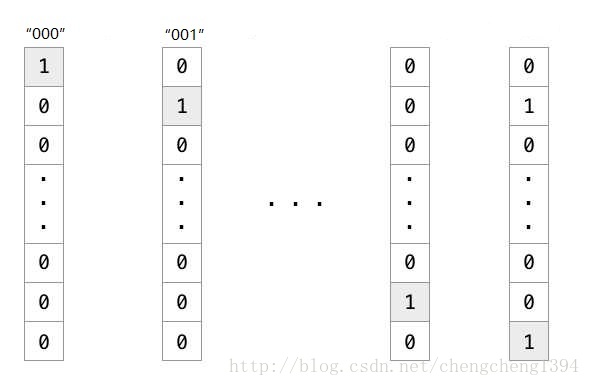
使用one hot稀疏向量在输入层与网络第一层做矩阵乘法时会很没有效率，因为向量里面大部分都是0， 矩阵乘法浪费了大量的计算，最终矩阵运算得出的结果是向量中值为1的列所对应的矩阵中的行向量。

图片来源
这看起来很像用索引查表一样，one hot向量中值为1的位置作为下标，去索引参数矩阵中的行向量。
为了代替矩阵乘法，我们将参数矩阵当作一个查找表（lookup table）或者叫做嵌入矩阵（embedding matrix），将每组开奖数据所对应的数作为索引，比如“958”，对应索引就是958，然后在查找表中找第958行。

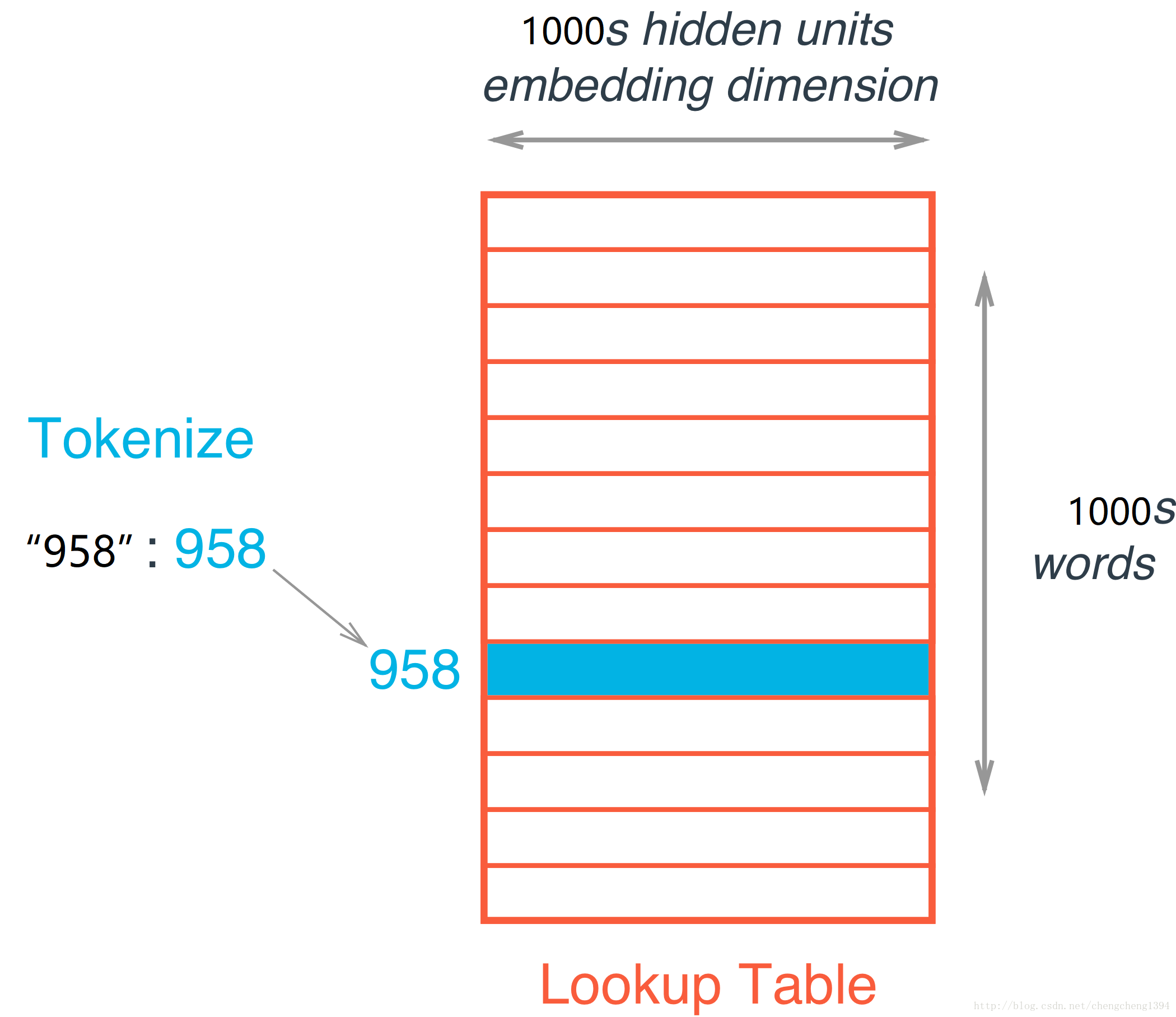
这其实跟替换之前的模型没有什么不同，嵌入矩阵就是参数矩阵，嵌入层仍然是隐层。查找表只是矩阵乘法的一种便捷方式，它会像参数矩阵一样被训练，是要学习的参数。
下面就是我们要构建的网络架构，从嵌入层输出的向量进入LSTM层进行时间序列的学习，然后经过softmax预测出下一期的开奖结果。

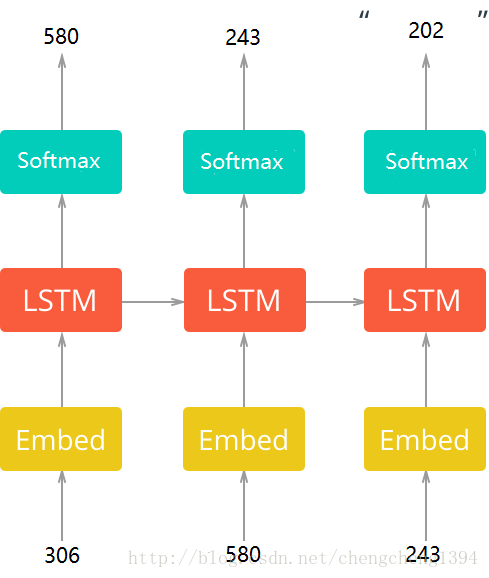
网络训练的代码，使用了几个trick，在下文<构建计算图>和<训练>章节会做说明，<结论>在最后。

主要代码讲解

完整代码请参见项目地址。

实现数据预处理

首先要做的事是对数据进行预处理，要实现下面的函数：
Lookup Table

使用词向量之前，我们需要先准备好单词(彩票开奖记录)和ID之间的转换关系。在这个函数中，创建并返回两个字典：

• 单词到ID的转换字典： vocab_to_int
• ID到单词的转换字典： int_to_vocab

import numpy as np
from collections import Counter

def create_lookup_tables():
    """
    Create lookup tables for vocabulary
    :param text: The text of tv scripts split into words
    :return: A tuple of dicts (vocab_to_int, int_to_vocab)
    """
    vocab_to_int = {str(ii).zfill(3) : ii for ii in range(1000)}
    int_to_vocab = {ii : str(ii).zfill(3) for ii in range(1000)}
    return vocab_to_int, int_to_vocab

构建神经网络

输入

def get_inputs():
    """
    Create TF Placeholders for input, targets, and learning rate.
    :return: Tuple (input, targets, learning rate)
    """
    inputs = tf.placeholder(tf.int32, [None, None], name="input")
    targets = tf.placeholder(tf.int32, [None, None], name="targets")
    LearningRate = tf.placeholder(tf.float32)
    return inputs, targets, LearningRate

构建RNN单元并初始化
将一个或多个BasicLSTMCells 叠加在MultiRNNCell中，这里我们使用2层LSTM cell。

def get_init_cell(batch_size, rnn_size):
    """
    Create an RNN Cell and initialize it.
    :param batch_size: Size of batches
    :param rnn_size: Size of RNNs
    :return: Tuple (cell, initialize state)
    """
    lstm_cell = tf.contrib.rnn.BasicLSTMCell(rnn_size)#num_units=embed_dim
    cell = tf.contrib.rnn.MultiRNNCell([lstm_cell] * 2)
    InitialState = cell.zero_state(batch_size, tf.float32)
    InitialState = tf.identity(InitialState, name="initial_state")
    return cell, InitialState

词嵌入

• embed_matrix：嵌入矩阵，后面计算相似度(距离)的时候会用到。
• embed_layer：从嵌入矩阵（查找表）中索引到的向量。

def get_embed(input_data, vocab_size, embed_dim):
    """
    Create embedding for <input_data>.
    :param input_data: TF placeholder for text input.
    :param vocab_size: Number of words in vocabulary.
    :param embed_dim: Number of embedding dimensions
    :return: Tuple (Embedded input, embed_matrix)
    """
    embed_matrix = tf.Variable(tf.random_uniform([vocab_size, embed_dim], -1, 1))
    embed_layer = tf.nn.embedding_lookup(embed_matrix, input_data)
    return embed_layer, embed_matrix

构建RNN

def build_rnn(cell, inputs):
    """
    Create a RNN using a RNN Cell
    :param cell: RNN Cell
    :param inputs: Input text data
    :return: Tuple (Outputs, Final State)
    """
    Outputs, final_State = tf.nn.dynamic_rnn(cell, inputs, dtype=tf.float32)
    final_State = tf.identity(final_State, name="final_state")
    return Outputs, final_State

创建神经网络

• 使用 get_embed(input_data, vocab_size, embed_dim) 函数将 input_data应用在嵌入层中。
• 使用 cell 和 build_rnn(cell, inputs) 函数创建RNN 。
• 使用具有线性激活函数的全连接层，将 vocab_size 作为输出的维度。

def build_nn(cell, rnn_size, input_data, vocab_size, embed_dim):
    """
    Build part of the neural network
    :param cell: RNN cell
    :param rnn_size: Size of rnns
    :param input_data: Input data
    :param vocab_size: Vocabulary size
    :param embed_dim: Number of embedding dimensions
    :return: Tuple (Logits, FinalState, embed_matrix)
    """
    embed_layer, embed_matrix = get_embed(input_data, vocab_size, embed_dim)
    Outputs, final_State = build_rnn(cell, embed_layer)
    logits = tf.layers.dense(Outputs, vocab_size)
    return logits, final_State, embed_matrix

训练神经网络

超参

调整如下参数：

• num_epochs ：设置训练几代。
• batch_size ：批次大小。
• rnn_size ：RNN的大小（隐藏节点的维度）。
• embed_dim： 嵌入层的维度。
• seq_length： 序列的长度，始终为1。
• learning_rate： 学习率。
• show_every_n_batches： 是过多少batch以后打印训练信息。

# Number of Epochs
num_epochs = 25
# Batch Size
batch_size = 32
# RNN Size
rnn_size = 1000
# Embedding Dimension Size
embed_dim = 1000
# Sequence Length
seq_length = 1
# Learning Rate
learning_rate = 0.01
# Show stats for every n number of batches
show_every_n_batches = 10

save_dir = './save'

构建计算图

使用实现的神经网络构建计算图。
要说明的是优化损失的部分，这里要优化两个损失：
cost：损失函数没有使用softmax交叉熵，而是使用了sequence loss。
similar_loss：另外一个要优化的想法是，要让预测的结果与正确结果在嵌入矩阵中的特征向量尽量接近，即让两者距离越来越小。
得到了最终的损失：total_loss = cost + similar_loss
使用normalized_embedding做相似度上距离的计算。

from tensorflow.contrib import seq2seq

tf.reset_default_graph()
train_graph = tf.Graph()
with train_graph.as_default():
    vocab_size = len(int_to_vocab)
    input_text, targets, lr = get_inputs()
    input_data_shape = tf.shape(input_text)
    cell, initial_state = get_init_cell(input_data_shape[0], rnn_size)
    logits, final_state, embed_matrix = build_nn(cell, rnn_size, input_text, vocab_size, embed_dim)

    # Probabilities for generating words
    probs = tf.nn.softmax(logits, name='probs')

    # Loss function
    cost = seq2seq.sequence_loss(
        logits,
        targets,
        tf.ones([input_data_shape[0], input_data_shape[1]]))

    # We use the cosine distance:
    norm = tf.sqrt(tf.reduce_sum(tf.square(embed_matrix), 1, keep_dims=True))
    normalized_embedding = embed_matrix / norm

    probs_embeddings = tf.nn.embedding_lookup(normalized_embedding, tf.squeeze(tf.argmax(probs, 2)))#np.squeeze(probs.argmax(2))
    probs_similarity = tf.matmul(probs_embeddings, tf.transpose(normalized_embedding))

    y_embeddings = tf.nn.embedding_lookup(normalized_embedding, tf.squeeze(targets))
    y_similarity = tf.matmul(y_embeddings, tf.transpose(normalized_embedding))

    similar_loss = tf.reduce_mean(tf.abs(y_similarity - probs_similarity))
    total_loss = cost + similar_loss

    # Optimizer
    optimizer = tf.train.AdamOptimizer(lr)

    # Gradient Clipping
    gradients = optimizer.compute_gradients(total_loss)
    capped_gradients = [(tf.clip_by_value(grad, -1., 1.), var) for grad, var in gradients if grad is not None]  #clip_by_norm
    train_op = optimizer.apply_gradients(capped_gradients)

    # Accuracy
    correct_pred = tf.equal(tf.argmax(probs, 2), tf.cast(targets, tf.int64))
    accuracy = tf.reduce_mean(tf.cast(correct_pred, tf.float32), name='accuracy')

训练

在预处理过的数据上训练神经网络。
这里除了保存预测准确率之外，还保存了三类准确率：

• Top K准确率： 预测结果中，前K个结果的预测准确率。
• 与预测结果距离最近的Top K准确率： 先得到预测结果，使用嵌入矩阵计算与预测结果Top 1距离最近的相似度向量，取这个相似度向量中前K个结果的预测准确率。
• 浮动距离中位数范围K准确率：得到预测结果之后，计算正确结果在预测结果中的距离中位数，这个距离实际上是元素在向量中的位置与第一个元素位置的距离。这个距离数据告诉我们真正的结果在我们的预测向量中的位置在哪。每次训练之后，距离中位数都会有变化，所以是浮动的，当然也可以考虑使用众数或均值。使用中位数表示真正的结果通常会在我们的预测向量中大部分时候（平均、或者说更具代表性的）位置在哪。所以这个准确率就是以中位数为中心，范围K为半径预测准确的概率。

这里距离中位数准确率我分别在预测结果向量和与预测结果Top 1距离最近的相似度向量中都做了统计，从结果来看在相似度向量中的距离中位数准确率要稍好一些。
浮动距离中位数的概率越高，说明我们的模型训练的不好，理想情况下应该是Top K准确率越来越高，说明模型预测的越来越准确。一旦模型预测的很差，那么预测向量中一定会有一部分区域是热点区域，也就是距离中位数指示的区域，这样可以通过距离中位数来进行预测。我们使用距离中位数来帮助我们进行预测，相当于为预测做了第二套方案，一旦模型预测不准确的时候，可以尝试使用距离中位数来预测。
这三类准确率都是范围的，我们只能知道在某个范围内猜中的概率会高一些，但是到底是范围内的哪一个是准确值则很难说。

%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import seaborn as sns
import matplotlib.pyplot as plt

batches = get_batches(int_text[:-(batch_size+1)], batch_size, seq_length)
test_batches = get_batches(int_text[-(batch_size+1):], batch_size, seq_length)
top_k = 10
#预测结果的Top K准确率
topk_acc_list = []
topk_acc = 0
#与预测结果距离最近的Top K准确率
sim_topk_acc_list = []
sim_topk_acc = 0

#表示k值是一个范围，不像Top K是最开始的K个
range_k = 5
#以每次训练得出的距离中位数为中心，以范围K为半径的准确率，使用预测结果向量
floating_median_idx = 0
floating_median_acc_range_k = 0
floating_median_acc_range_k_list = []

#同上，使用的是相似度向量
floating_median_sim_idx = 0
floating_median_sim_acc_range_k = 0
floating_median_sim_acc_range_k_list = []

#保存训练损失和测试损失
losses = {'train':[], 'test':[]}
#保存各类准确率
accuracies = {'accuracy':[], 'topk':[], 'sim_topk':[], 'floating_median_acc_range_k':[], 'floating_median_sim_acc_range_k':[]}

with tf.Session(graph=train_graph) as sess:
    sess.run(tf.global_variables_initializer())
    saver = tf.train.Saver()
    for epoch_i in range(num_epochs):
        state = sess.run(initial_state, {input_text: batches[0][0]})

        #训练的迭代，保存训练损失
        for batch_i, (x, y) in enumerate(batches):
            feed = {
                input_text: x,
                targets: y,
                initial_state: state,
                lr: learning_rate}
            train_loss, state, _ = sess.run([total_loss, final_state, train_op], feed)  #cost
            losses['train'].append(train_loss)

            # Show every <show_every_n_batches> batches
            if (epoch_i * len(batches) + batch_i) % show_every_n_batches == 0:
                print('Epoch {:>3} Batch {:>4}/{}   train_loss = {:.3f}'.format(
                    epoch_i,
                    batch_i,
                    len(batches),
                    train_loss))

        #使用测试数据的迭代
        acc_list = []
        prev_state = sess.run(initial_state, {input_text: np.array([[1]])})
        for batch_i, (x, y) in enumerate(test_batches):
            # Get Prediction
            test_loss, acc, probabilities, prev_state = sess.run(
                [total_loss, accuracy, probs, final_state],
                {input_text: x, 
                 targets: y,
                 initial_state: prev_state})  

            #保存测试损失和准确率
            acc_list.append(acc)
            losses['test'].append(test_loss)
            accuracies['accuracy'].append(acc)

            print('Epoch {:>3} Batch {:>4}/{}   test_loss = {:.3f}'.format(
                epoch_i,
                batch_i,
                len(test_batches),
                test_loss))

            #利用嵌入矩阵和生成的预测计算得到相似度矩阵sim
            valid_embedding = tf.nn.embedding_lookup(normalized_embedding, np.squeeze(probabilities.argmax(2)))
            similarity = tf.matmul(valid_embedding, tf.transpose(normalized_embedding))
            sim = similarity.eval()

            #保存预测结果的Top K准确率和与预测结果距离最近的Top K准确率
            topk_acc = 0
            sim_topk_acc = 0
            for ii in range(len(probabilities)):

                nearest = (-sim[ii, :]).argsort()[0:top_k]
                if y[ii] in nearest:
                    sim_topk_acc += 1

                if y[ii] in (-probabilities[ii]).argsort()[0][0:top_k]:
                    topk_acc += 1

            topk_acc = topk_acc / len(y)
            topk_acc_list.append(topk_acc)
            accuracies['topk'].append(topk_acc)

            sim_topk_acc = sim_topk_acc / len(y)
            sim_topk_acc_list.append(sim_topk_acc)
            accuracies['sim_topk'].append(sim_topk_acc)

            #计算真实值在预测值中的距离数据
            realInSim_distance_list = []
            realInPredict_distance_list = []
            for ii in range(len(probabilities)):
                sim_nearest = (-sim[ii, :]).argsort()
                idx = list(sim_nearest).index(y[ii])
                realInSim_distance_list.append(idx)

                nearest = (-probabilities[ii]).argsort()[0]
                idx = list(nearest).index(y[ii])
                realInPredict_distance_list.append(idx)

            print('真实值在预测值中的距离数据：')
            print('max distance : {}'.format(max(realInPredict_distance_list)))
            print('min distance : {}'.format(min(realInPredict_distance_list)))
            print('平均距离 : {}'.format(np.mean(realInPredict_distance_list)))
            print('距离中位数 : {}'.format(np.median(realInPredict_distance_list)))
            print('距离标准差 : {}'.format(np.std(realInPredict_distance_list)))

            print('真实值在预测值相似向量中的距离数据：')
            print('max distance : {}'.format(max(realInSim_distance_list)))
            print('min distance : {}'.format(min(realInSim_distance_list)))
            print('平均距离 : {}'.format(np.mean(realInSim_distance_list)))
            print('距离中位数 : {}'.format(np.median(realInSim_distance_list)))
            print('距离标准差 : {}'.format(np.std(realInSim_distance_list)))

            #计算以距离中位数为中心，范围K为半径的准确率
            floating_median_sim_idx = int(np.median(realInSim_distance_list))
            floating_median_sim_acc_range_k = 0

            floating_median_idx = int(np.median(realInPredict_distance_list))
            floating_median_acc_range_k = 0
            for ii in range(len(probabilities)):
                nearest_floating_median = (-probabilities[ii]).argsort()[0][floating_median_idx - range_k:floating_median_idx + range_k]
                if y[ii] in nearest_floating_median:
                    floating_median_acc_range_k += 1

                nearest_floating_median_sim = (-sim[ii, :]).argsort()[floating_median_sim_idx - range_k:floating_median_sim_idx + range_k]
                if y[ii] in nearest_floating_median_sim:
                    floating_median_sim_acc_range_k += 1

            floating_median_acc_range_k = floating_median_acc_range_k / len(y)
            floating_median_acc_range_k_list.append(floating_median_acc_range_k)
            accuracies['floating_median_acc_range_k'].append(floating_median_acc_range_k)

            floating_median_sim_acc_range_k = floating_median_sim_acc_range_k / len(y)
            floating_median_sim_acc_range_k_list.append(floating_median_sim_acc_range_k)
            accuracies['floating_median_sim_acc_range_k'].append(floating_median_sim_acc_range_k)

        print('Epoch {:>3} floating median sim range k accuracy {} '.format(epoch_i, np.mean(floating_median_sim_acc_range_k_list)))#:.3f
        print('Epoch {:>3} floating median range k accuracy {} '.format(epoch_i, np.mean(floating_median_acc_range_k_list)))#:.3f
        print('Epoch {:>3} similar top k accuracy {} '.format(epoch_i, np.mean(sim_topk_acc_list)))#:.3f
        print('Epoch {:>3} top k accuracy {} '.format(epoch_i, np.mean(topk_acc_list)))#:.3f
        print('Epoch {:>3} accuracy {} '.format(epoch_i, np.mean(acc_list)))#:.3f

    # Save Model
    saver.save(sess, save_dir) 
    print('Model Trained and Saved')
    embed_mat = sess.run(normalized_embedding)

最后一次迭代输出的结果：

真实值在预测值中的距离数据：
max distance : 998
min distance : 9
平均距离 : 534.59375
距离中位数 : 489.0
距离标准差 : 299.3345598338713
真实值在预测值相似向量中的距离数据：
max distance : 988
min distance : 1
平均距离 : 505.28125
距离中位数 : 443.5
距离标准差 : 297.11700498025607
Epoch  24 floating median sim range k accuracy 0.0325 
Epoch  24 floating median range k accuracy 0.01125 
Epoch  24 similar top k accuracy 0.0275 
Epoch  24 top k accuracy 0.025 
Epoch  24 accuracy 0.0 

距离图表

真实值在预测值相似向量中的距离数据：
距离中位数 : 443.5
距离标准差 : 297.11700498025607

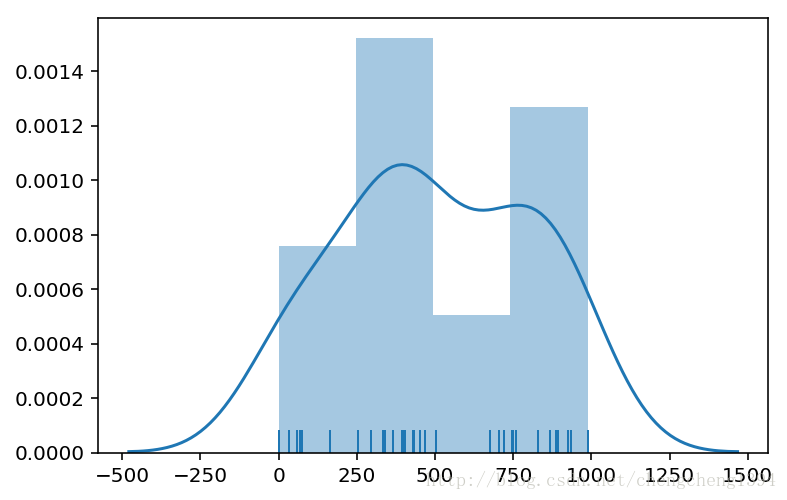
真实值在预测值中的距离数据：
距离中位数 : 489.0
距离标准差 : 299.3345598338713

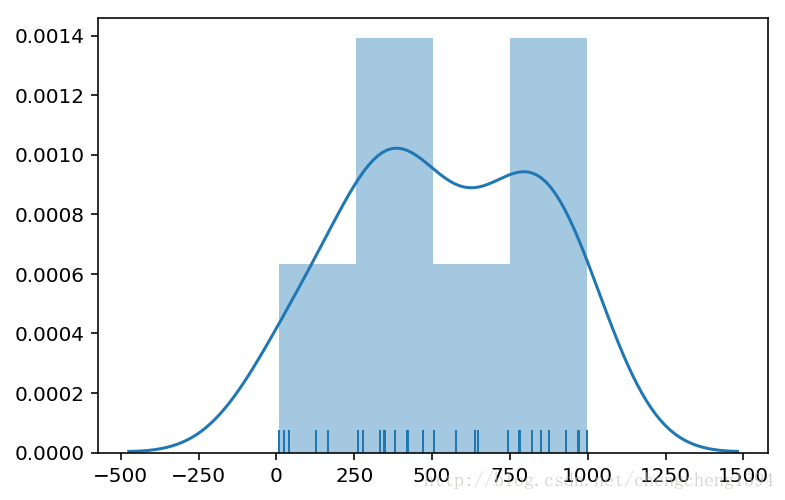
从最后一次的距离图表来看，跟训练得出的数据还是比较吻合的，双峰一个对应了中位数，另一个对应着中位数+标准差。说明模型训练的还不够好，不过可以用中位数来弥补预测的不足。

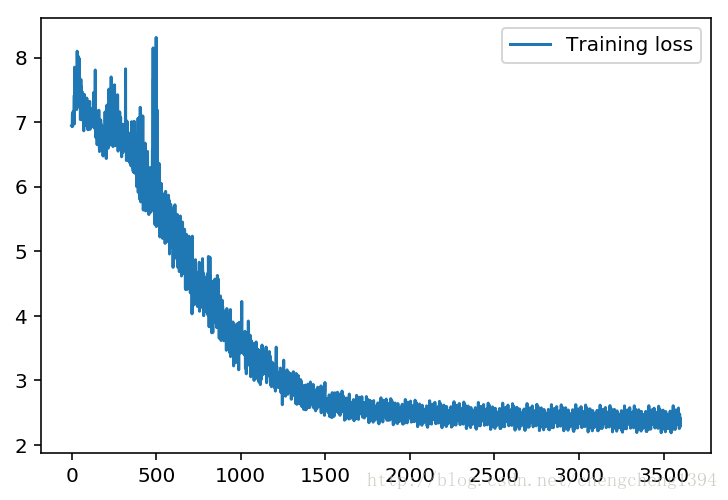
显示训练Loss

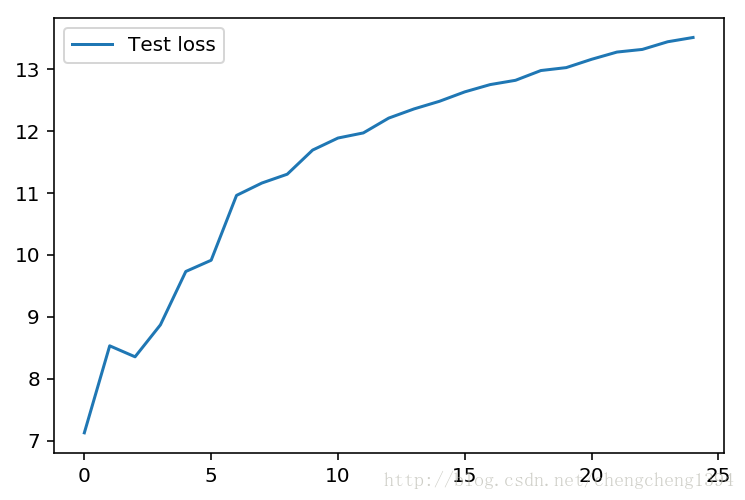
显示测试Loss

测试损失始终没有降下去。。。，epochs高一点的话会出现下降-上升-下降的波浪形曲线。

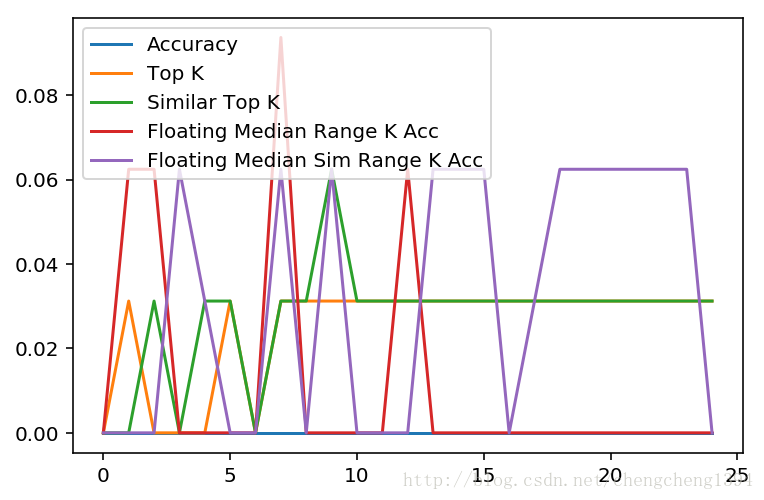
显示准确率

• 测试准确率
• Top K准确率
• 相似度Top K准确率
• 浮动距离中位数Range K准确率
  

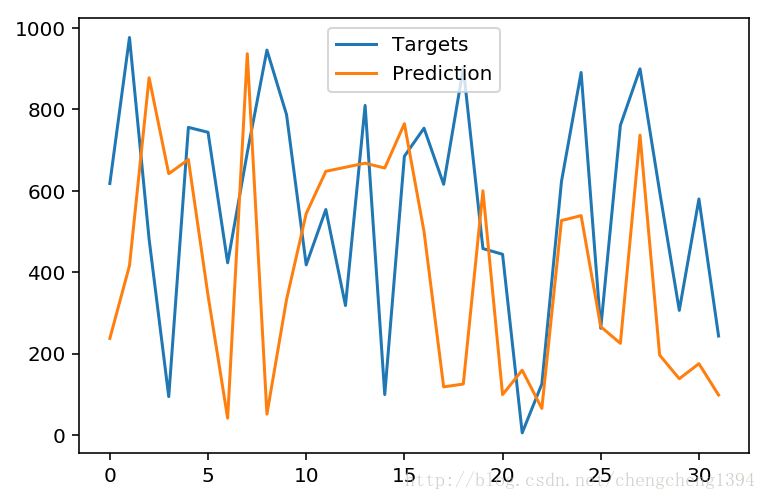
显示预测结果和实际开奖结果

感觉从趋势上看起来还行，实际结果是一个都没有猜中 ：P
有的简直错的离谱，南辕北辙

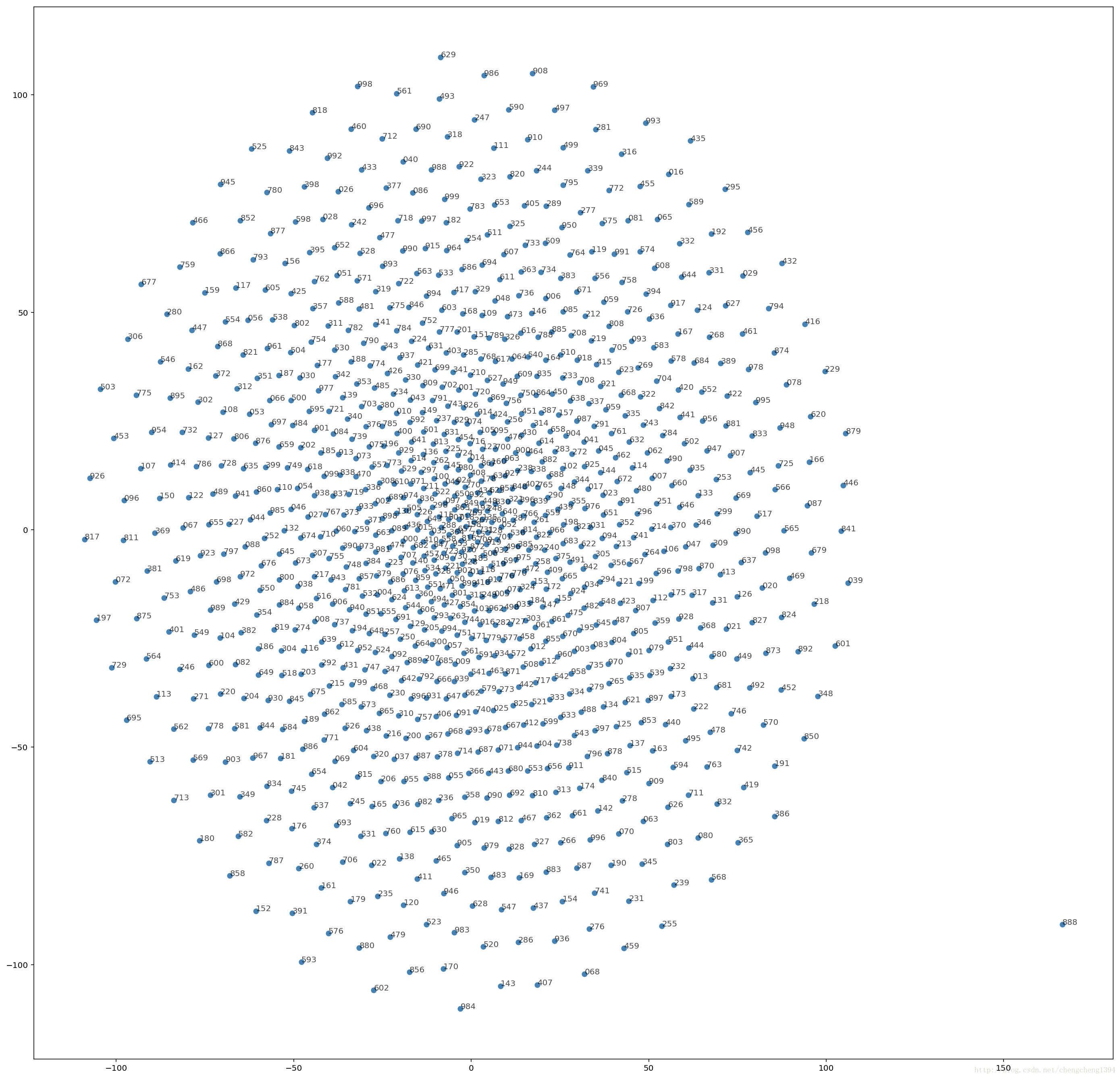
往期开奖结果的相似度分布

在训练不够充分的情况下，从往期开奖的相互之间的距离图可以看出，大部分的数据点相互之间的距离基本上都差不多，完全符合彩票随机的特性，出现任何一种结果的概率都是一样的。甚至上一期和下一期之间的距离也有可能间隔非常远，只有一部分数据点之间联系的比较紧密，这部分数据点我们还可以试试运气。
迭代100次的话，你会看到如下的距离图：

实现生成预测函数

选择号码

实现 pick_word() 函数从概率向量 probabilities或相似度向量sim中选择号码。
pred_mode是选择预测的种类：

• sim：从相似度向量Top K中选号。
• median：从浮动距离中位数（相似度向量）Range K中选号。
• topk：从概率向量Top K中选号。
• max：从概率向量中选择最大概率的号码。

def pick_word(probabilities, sim, int_to_vocab, top_n = 5, pred_mode = 'sim'):

    vocab_size = len(int_to_vocab)

    if pred_mode == 'sim':
        p = np.squeeze(sim)
        p[np.argsort(p)[:-top_n]] = 0
        p = p / np.sum(p)
        c = np.random.choice(vocab_size, 1, p=p)[0]
        return int_to_vocab[c]
    elif pred_mode == 'median':
        p = np.squeeze(sim)
        p[np.argsort(p)[:floating_median_sim_idx - top_n]] = 0
        p[np.argsort(p)[floating_median_sim_idx + top_n:]] = 0
        p = np.abs(p) / np.sum(np.abs(p))
        c = np.random.choice(vocab_size, 1, p=p)[0]
        return int_to_vocab[c]
    elif pred_mode == 'topk':
        p = np.squeeze(probabilities)
        p[np.argsort(p)[:-top_n]] = 0
        p = p / np.sum(p)
        c = np.random.choice(vocab_size, 1, p=p)[0]
        return int_to_vocab[c]
    elif pred_mode == 'max':
        return int_to_vocab[probabilities.argmax()]

生成号码

开始进行预测了。

• gen_length 为你想生成多少期的号码。
• prime_word 是前一期号码

gen_length = 17
prime_word = '202'

loaded_graph = tf.Graph()  #loaded_graph
with tf.Session(graph=train_graph) as sess:
    # Load saved model
    loader = tf.train.import_meta_graph(load_dir + '.meta')
    loader.restore(sess, load_dir)

    # Get Tensors from loaded model
    input_text, initial_state, final_state, probs = get_tensors(train_graph)  #loaded_graph

    # Sentences generation setup
    gen_sentences = [prime_word]
    prev_state = sess.run(initial_state, {input_text: np.array([[1]])})

    # Generate sentences
    for n in range(gen_length):
        # Dynamic Input
        dyn_input = [[vocab_to_int[word] for word in gen_sentences[-seq_length:]]]
        dyn_seq_length = len(dyn_input[0])

        # Get Prediction
        probabilities, prev_state = sess.run(
            [probs, final_state],
            {input_text: dyn_input, initial_state: prev_state})

        valid_embedding = tf.nn.embedding_lookup(normalized_embedding, probabilities.argmax())
        valid_embedding = tf.reshape(valid_embedding, (1, len(int_to_vocab)))
        similarity = tf.matmul(valid_embedding, tf.transpose(normalized_embedding))
        sim = similarity.eval()

        pred_word = pick_word(probabilities[dyn_seq_length-1], sim, int_to_vocab, 5, 'median')

        gen_sentences.append(pred_word)

    cp_script = ' '.join(gen_sentences)
    cp_script = cp_script.replace('n ', 'n')
    cp_script = cp_script.replace('( ', '(')

    print(cp_script)

预测出的号码：202 526 164 739 151 015 196 670 193 425 015 270 472 915 549 191 958 419

结论

先从数据上说，训练的最后打印出的准确率如下：

Epoch 24 floating median sim range k accuracy 0.0325
Epoch 24 floating median range k accuracy 0.01125
Epoch 24 similar top k accuracy 0.0275
Epoch 24 top k accuracy 0.025
Epoch 24 accuracy 0.0

正常的开奖概率是1‰。
经过25次迭代训练之后准确率是0，一个都没猜中。。。
top k和相似度向量top k差不多，都是25‰左右，但因为是top 10，所以实际上是2.5‰左右。
浮动中位数准确率在11.25‰~32.5‰之间，但由于这个范围range 10，所以实际上是1.125~3.25‰之间。
最好的时刻是在Epoch 2 floating median range k accuracy 0.041666666666666664，也就是4.16‰。
真没比正常开奖概率好多少。
从训练结果打印出的准确率，和往期开奖的相互之间的距离图都可以看得出来，想进行彩票预测实际上是不可行的。在排列三如此简单的、排列组合只有1000(样本空间已经足够小了)的等概率事件上进行预测都如此的困难，这也印证了数学的奇妙之处。都说了彩票是等概率，那么出任何一种号码都是有可能的，没有规律可言。惊不惊喜？意不意外？

新的思路

既然不能准确的预测，唯一能给我们提供思路的就是学习器学到的趋势，来看看下面的代码。

• int_sentences：里面保存着上面生成的若干期号码
• val_data：是最新几期的开奖号码，作为validate数据集

int_sentences = [int(words) for words in gen_sentences]
int_sentences = int_sentences[1:]

val_data = [[103],[883],[939],[36],[435],[173],[572],[828],[509],[723],[145],[621],[535],[385],[98],[321],[427]]
plt.plot(int_sentences, label='History')
plt.plot(val_tests, label='val_data')
plt.legend()
_ = plt.ylim()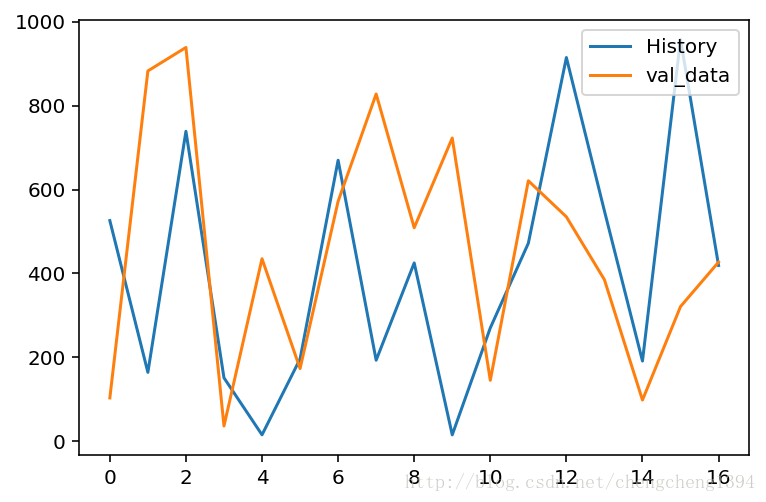

看得出来，虽然每期预测的号码不对，但是下一期号码的大概范围以及若干期号码的变化趋势学习的还可以，剩下的就要靠运气了：）
看看最后一期的号码是427，我们预测的是419，是不是很接近？

如果您有更好的想法，或者想挑战我的预测结果，欢迎在下面留言或email我 ^_^

今天的分享就到这里，大家洗洗睡吧 ：）

最后

以上就是自觉寒风为你收集整理的TensorFlow实战——使用LSTM预测彩票前言LSTM介绍看看数据集的结构预测网络介绍主要代码讲解训练神经网络结论的全部内容，希望文章能够帮你解决TensorFlow实战——使用LSTM预测彩票前言LSTM介绍看看数据集的结构预测网络介绍主要代码讲解训练神经网络结论所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。