概述
文章目录
- 一、理论基础
- 1、标准鲸鱼优化算法
- 2、改进鲸鱼优化算法
- （1）自适应惯性权重
- （2）镜像选择
- 二、WOA-MS算法流程图
- 三、仿真实验与结果分析
- 四、参考文献
一、理论基础
1、标准鲸鱼优化算法
请参考这里。
2、改进鲸鱼优化算法
针对鲸鱼优化算法容易陷入局部最优解且收敛速度慢的问题，提出了一种改进的基于镜像选择的鲸鱼优化算法(WOA-MS)，采用两种改进的方法，从理论上提高了算法的整体性能不同的方面。
（1）自适应惯性权重
在WOA中引入了惯性权重的概念。在迭代开始时，算法应着眼于全局搜索；在迭代的后半部分，算法应注重局部挖掘。因此，惯性权重的值应随着迭代次数的增加而减小。为了实现惯性权重的动态变化，本文引入Branin函数来构造惯性权重。
Branin是一个二维复合函数，其图像是不均匀的。它的函数表达式是：
f
(
x
,
y
)
=
(
y
−
5.1
4
π
2
x
2
+
5
π
x
−
6
)
2
+
10
(
1
−
1
8
π
)
cos
x
+
10
(1)
f(x,y)=left(y-frac{5.1}{4pi^2}x^2+frac5pi x-6right)^2+10left(1-frac1{8pi}right)cos x+10tag{1}
f(x,y)=(y−4π25.1x2+π5x−6)2+10(1−8π1)cosx+10(1)为了实现上述惯性权重的动态调整效果，本文将Branin函数转化为
f
(
x
,
y
)
=
[
(
y
−
5.1
4
π
2
x
2
+
5
π
x
−
6
)
2
+
10
(
1
−
1
8
π
)
cos
(
−
x
)
+
10
]
100
(2)
f(x,y)=frac{left[left(y-frac{5.1}{4pi^2}x^2+frac5pi x-6right)^2+10left(1-frac1{8pi}right)cos(-x)+10right]}{100}tag{2}
f(x,y)=100[(y−4π25.1x2+π5x−6)2+10(1−8π1)cos(−x)+10](2)改变后的函数图像如图1所示。
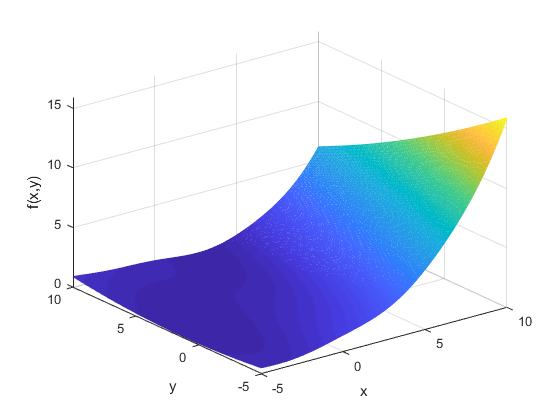
自适应惯性权重计算过程如下：
（1）在迭代过程的每一代中，每个维度的平均值向量计算如下：
X
a
v
g
(
j
)
=
∑
i
=
1
N
X
(
i
,
j
)
/
N
(3)
boldsymbol X_{avg}(j)=sum_{i=1}^Nboldsymbol X(i,j)/Ntag{3}
Xavg(j)=i=1∑NX(i,j)/N(3)其中，
X
(
i
,
j
)
boldsymbol X(i, j)
X(i,j)表示第
i
i
i头鲸在第
j
j
j个维度上的位置；
N
N
N表示种群规模。
（2）计算种群中每个个体的距离，它是由每个维度的平均值计算得出的。
d
(
j
)
=
∣
X
(
j
)
−
X
a
v
g
(
j
)
∣
(4)
boldsymbol d(j)=|boldsymbol X(j)-boldsymbol X_{avg}(j)|tag{4}
d(j)=∣X(j)−Xavg(j)∣(4)其中，
X
(
j
)
boldsymbol X(j)
X(j)表示种群在第
j
j
j维上的位置向量。
（3）
X
boldsymbol X
X和
y
boldsymbol y
y由公式(13)(14)计算得到，再代入公式(2)得到
f
(
j
)
boldsymbol f(j)
f(j)。
x
=
d
(
j
)
d
m
a
x
(
j
)
+
1
0
−
200
(5)
boldsymbol x=frac{boldsymbol d(j)}{boldsymbol d_{max}(j)+10^{-200}}tag{5}
x=dmax(j)+10−200d(j)(5)
y
=
t
T
(6)
boldsymbol y=frac tTtag{6}
y=Tt(6)其中，
f
(
j
)
boldsymbol f(j)
f(j)表示第
j
j
j维种群中个体的惯性权重向量；
T
T
T代表最大迭代次数；
d
m
a
x
(
j
)
boldsymbol d_{max}(j)
dmax(j)表示所有个体与第
j
j
j维上的平均值之间的最远距离。自适应Branin系数函数的图像如图2所示。
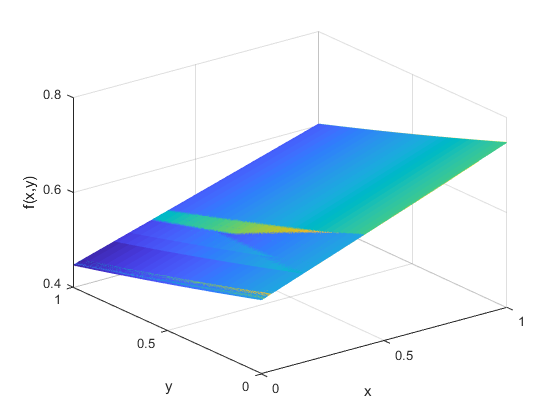
之后根据公式(7)(8)(9)进行位置更新。
X
(
t
+
1
)
=
F
(
t
)
⋅
X
r
a
n
d
−
A
⋅
D
(7)
boldsymbol X(t+1)=boldsymbol F(t)cdotboldsymbol X_{rand}-boldsymbol{Acdot D}tag{7}
X(t+1)=F(t)⋅Xrand−A⋅D(7)
X
(
t
+
1
)
=
F
(
t
)
⋅
X
∗
(
t
)
−
A
⋅
D
(8)
boldsymbol X(t+1)=boldsymbol F(t)cdotboldsymbol X^*(t)-boldsymbol{Acdot D}tag{8}
X(t+1)=F(t)⋅X∗(t)−A⋅D(8)
X
(
t
+
1
)
=
X
∗
(
t
)
+
F
(
t
)
⋅
D
e
b
l
cos
(
2
π
l
)
(9)
boldsymbol X(t+1)=boldsymbol X^*(t)+boldsymbol F(t)cdotboldsymbol De^{bl}cos(2pi l)tag{9}
X(t+1)=X∗(t)+F(t)⋅Deblcos(2πl)(9)其中，
F
(
t
)
boldsymbol F(t)
F(t)表示每个维度上个体第
t
t
t代的惯性权重向量。
该方法在迭代初期更新的惯性权重较大，有利于全局搜索；在迭代后期，权重减小，这有利于局部的开发。
（2）镜像选择
镜像选择策略是通过镜像方法对整个种群进行变异的一种策略。它可以大大增加种群的多样性，但同时也增加了种群中的个体数量。因此，选择变异后的个体作为下一代迭代的输入，以增强种群的多样性，提高个体质量，加快收敛速度。镜像选择策略可分为镜像变异和优胜劣汰两部分。具体来说根据公式(10)来产生对称(镜像)解。
X
(
t
)
′
=
B
u
+
B
l
−
X
(
t
)
(10)
boldsymbol X(t)'=boldsymbol B_u+boldsymbol B_l-boldsymbol X(t)tag{10}
X(t)′=Bu+Bl−X(t)(10)其中，
X
(
t
)
′
boldsymbol X(t)'
X(t)′表示镜像独立个体的位置；
B
u
boldsymbol B_u
Bu和
B
l
boldsymbol B_l
Bl表示单个上下限向量；
X
(
t
)
boldsymbol X(t)
X(t)表示原始独立个体位置向量。
之后，种群数量增加到原来的两倍，然后进行“优胜劣汰”。新生成的镜像解与原始解合并，并根据适应度进行排序，选择适合度排名前
N
N
N的个体作为首选个体，进入下一次计算和迭代。
二、WOA-MS算法流程图
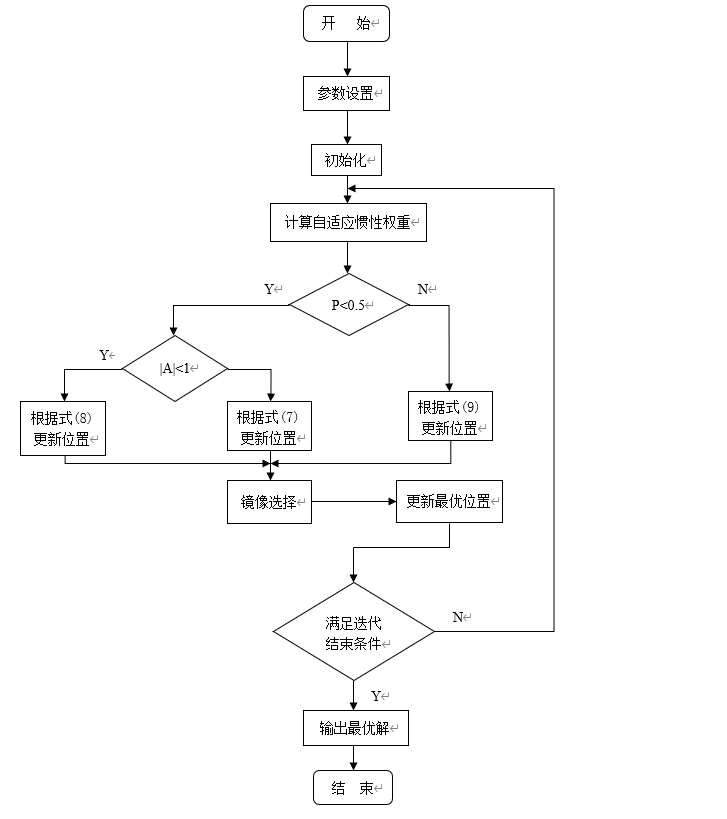
三、仿真实验与结果分析
本文对标准粒子群优化算法、标准WOA算法、改进粒子群优化算法(IPSO)和WOA-MS算法进行了比较，其中IPSO算法的改进措施包括加入动态自学习因子
c
1
c_1
c1、动态群学习因子
c
2
c_2
c2和动态惯性权重
w
w
w，并在相同参数下对WOA-MS算法的性能进行了测试。
12个基准函数图形如图4所示。
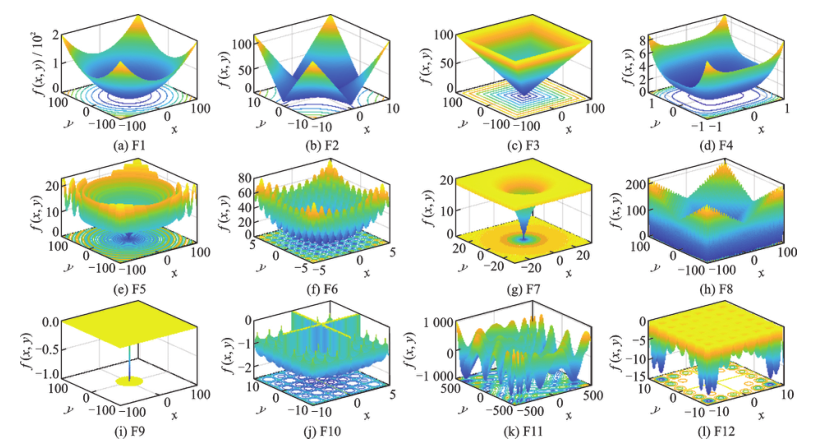
以F1、F2、F3为例。
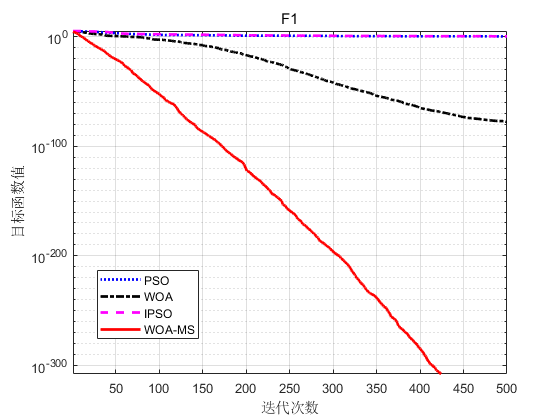
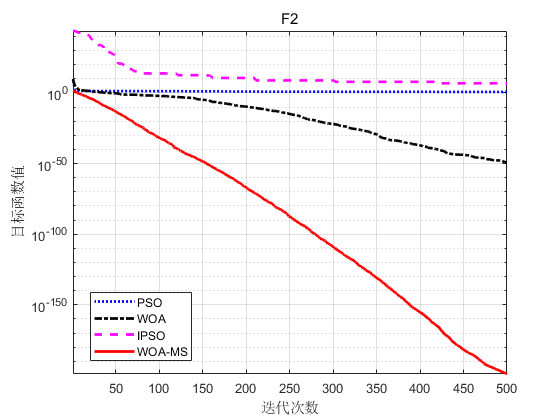
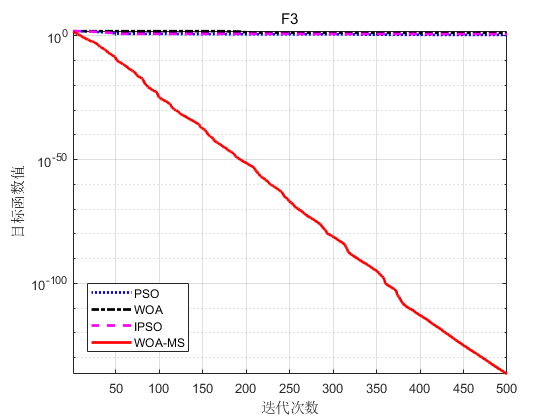仿真结果表明：
（1） WOA-MS具有良好的种群多样性。WOA-MS引入了自适应惯性权重，很好地平衡了全局搜索和局部搜索。因此，在优化过程中，不存在种群高度集中、多样性急剧降低的现象，同时保持多样性以提高全局搜索能力。
（2） WOA-MS算法收敛速度快，局部搜索能力强。镜像选择方法大大提高了每一代的个体质量，加快了算法的收敛速度，提高了局部寻优效率。总之，与其他三种传统算法相比，WOA-MS具有优异的全局优化性能。
四、参考文献
[1] 田东平, 赵天绪. 基于群体适应度方差的自适应粒子群优化算法[J]. 计算机工程与应用, 2010, 46(18):24-26.
[2] LI Jingnan, LE Meilong. Improved whale optimization algorithm based on mirror selection[J]. Transactions of Nanjing University of Aeronautics and Astronautics, 2020, 37(S): 115-123.
最后
以上就是美满母鸡为你收集整理的基于镜像选择的改进鲸鱼优化算法一、理论基础二、WOA-MS算法流程图三、仿真实验与结果分析四、参考文献的全部内容，希望文章能够帮你解决基于镜像选择的改进鲸鱼优化算法一、理论基础二、WOA-MS算法流程图三、仿真实验与结果分析四、参考文献所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复