1. 首页
  2. 文章中心
  3. Modelsim

独热码状态机，SR锁存器延迟模型，移位除法器模型

110 阅读 0 评论
我是靠谱客的博主 醉熏小懒虫，这篇文章主要介绍独热码状态机，SR锁存器延迟模型，移位除法器模型，现在分享给大家，希望可以做个参考。

独热码状态机

进行时序电路设计时，一般都要根据设计要求画出状态转换图，然后根据状态图来确定如何编写代码。

  • 该实例状态转换图如下
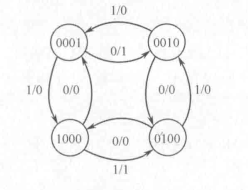
    状态转换图
  • 编写模块代码如下
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
module ex8_1(clock,reset,x,y1,y2);
input clock,reset;
input x;
output y1,y2;
reg y1,y2;

reg[3:0] cstate,nstate;

parameter s0=4'b0001,s1=4'b0010,	//本例中采用独热码，当然使用二进制码也可
		s2=4'b0100,s3=4'b1000;
		
always @(posedge clock or posedge reset)	//第一段always，原态变新态
begin
	if(reset)
		cstate<=s0;
	else
		cstate<=nstate;
end

always @(cstate or x)		//第二段always,状态转换
begin
	case(cstate)
	s0:begin
		if(x==0)
			nstate=s1;
		else
			nstate=s3;
	   end
	s1:begin
		if(x==0)
			nstate=s2;
		else
			nstate=s0;
	   end
	s2:begin
		if(x==0)
			nstate=s3;
		else
			nstate=s1;
	   end
	s3:begin
		if(x==0)
			nstate=s0;
		else
			nstate=s2;
	   end
	default:nstate=s0;
	endcase
end
always @(cstate or x)		//第三段always，产生输出
begin
	case(cstate)
	s0:begin
		if(x==0)
			y1=1;
		else
			y1=0;
	   end
	s1:begin
		if(x==0)
			y1=0;
		else
			y1=0;
	   end
	s2:begin
		if(x==0)
			y1=0;
		else
			y1=0;
	   end
	s3:begin
		if(x==0)
			y1=0;
		else
			y1=1;
	   end
	default:y1=0;
	endcase
end
always @(cstate or x)		//在输出比较简单时，也可以使用if来确定输出值
begin
	if(cstate==s0 && x==0)		//本段always功能与上段相同，但明显简洁易懂
		y2=1;
	else if(cstate==s3 && x==1)	//两种y2=1,发生的情况也可以合并成一种
		y2=1;
	else if(cstate==s3  && x==1)
		y2=1;
	else
		y2=0;
end
endmodule

在本例中使用了两个输出y1和y2，y2是一个简化输出，用来描述在两种情况下输出1值，其他情况下输出都是0值，如果结合括号使用，还可以进一步精简写成如下形式。

复制代码
1
2
3
4
5
6
7
8
always @(cstate or x)
begin
	if((cstate==s0 && x==0) || (cstate==s3 && x==1))	//合并输出
		y2=1;
	else
		y2=0;
end
  • 编写测试模块代码如下：
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
module tb_ex81;
reg x,clock,reset;
wire y1,y2;

initial clock=0;
always #5 clock=~clock;

initial
begin
	reset=0;
	#15 reset=1;
	#15 reset=0;
	#10000 $stop;
end

initial
begin
	#10 x=1;
	#500 x=0;
end

ex8_1  myex81(clock,reset,x,y1,y2);

endmodule

运行可得仿真波形图如下所示。

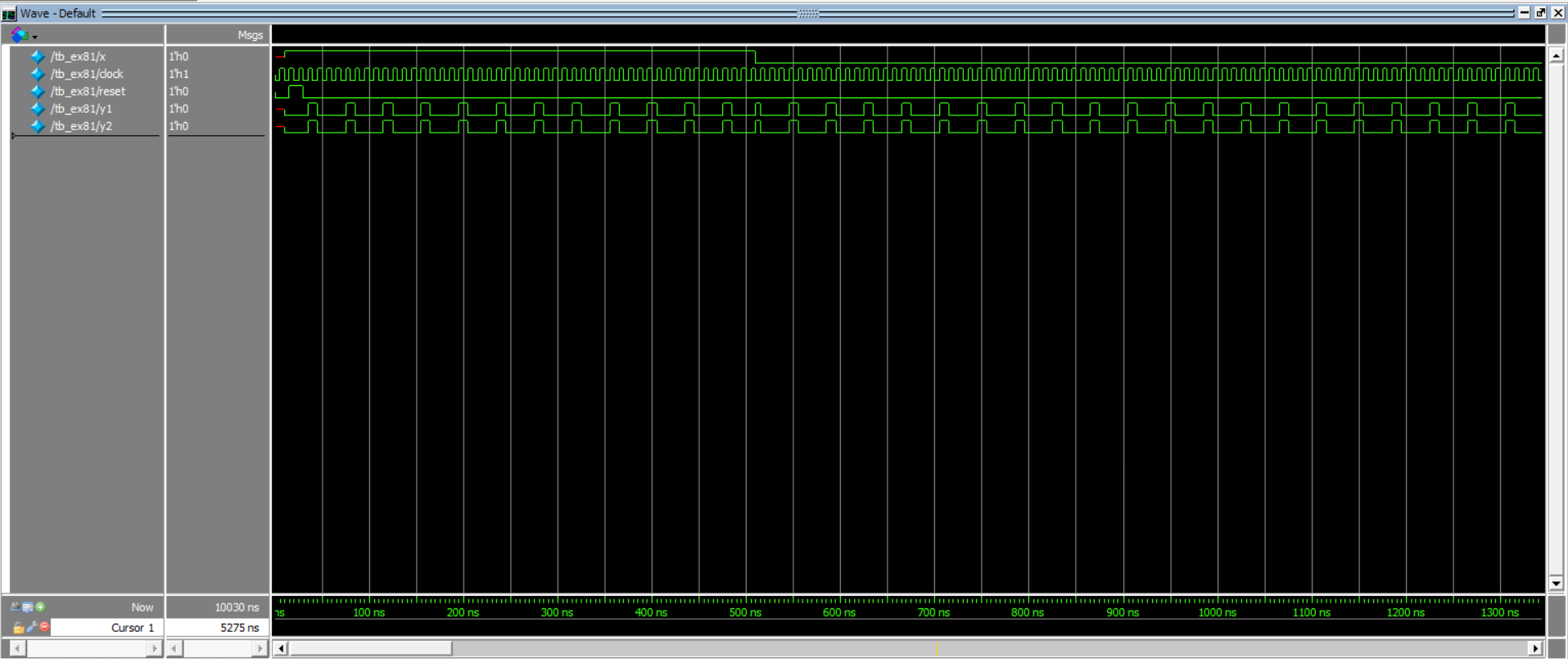
独热码状态机仿真图

SR锁存器延迟模型

采用门级建模语句实现一个SR锁存器， 主要体现延迟时间的问题，基本SR锁存器的电路图如图所示。

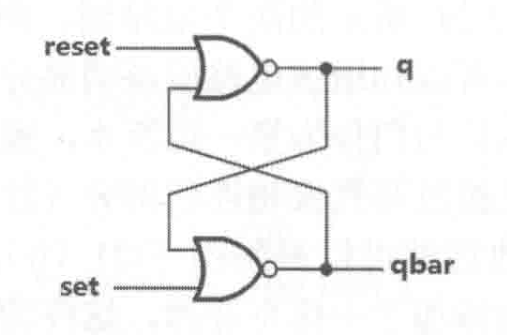
SR锁存器电路图

  • 添加门级延迟，对其建模如下：
复制代码
1
2
3
4
5
6
7
8
9
module my_rs(reset,set,q,qbar);
input reset,set;
output q,qbar;

nor#(1) n1(q,reset,qbar);
nor#(1) n2(qbar,set,q);

endmodule
  • 编写测试模块如下
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
module tb_71;
reg set,reset;
wire q,qbar;

initial
begin
	set<=0;reset<=1;
#10 set<=0;reset<=0;
#10 set<=1;reset<=0;
#10 set<=1;reset<=1;
end
my_rs rsl(reset,set,q,qbar);

initial
$monitor($time,"set= %b,reset= %b,q= %b,qbar= %b",set,reset,q,qbar);

endmodule

运行可得如图所示的仿真结果，该结果对应典型延迟时间。
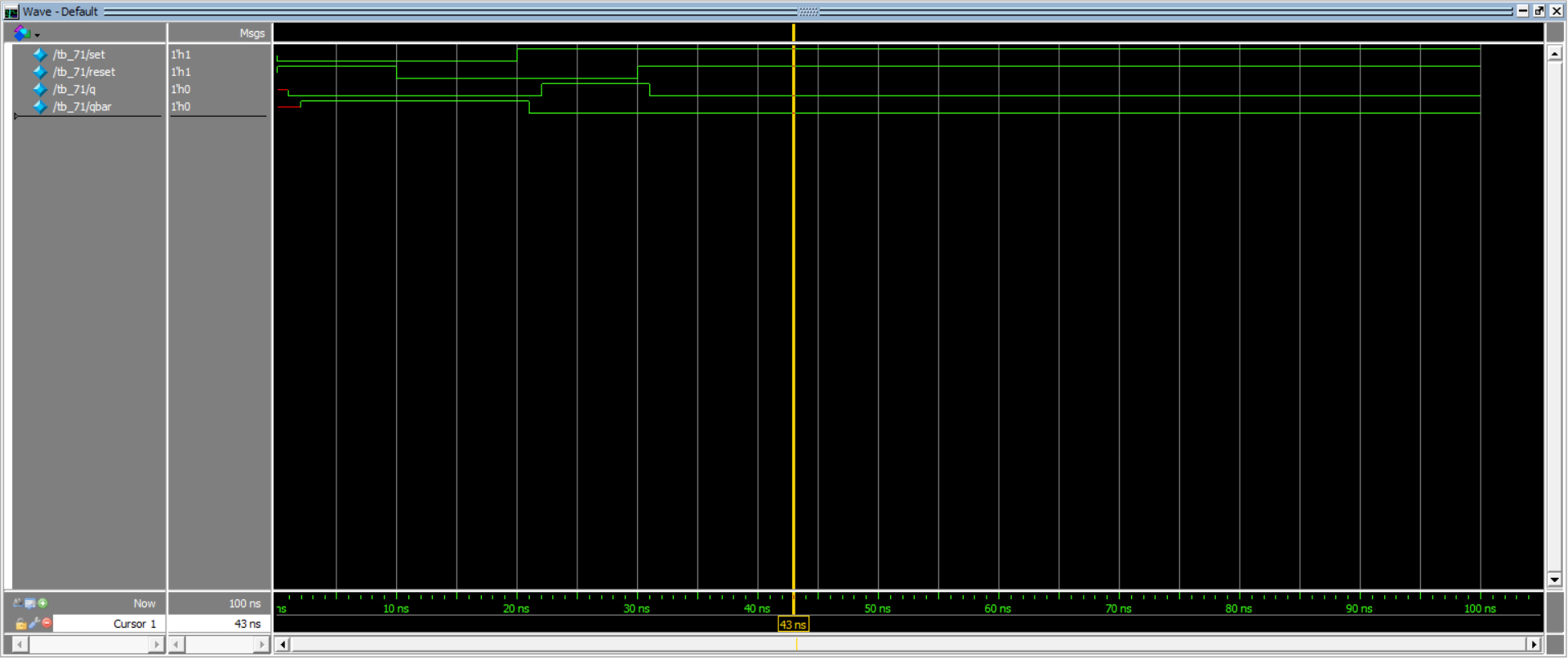
SR锁存器仿真图

仿真输出如下

复制代码
1
2
3
4
5
6
7
8
9
10
#                    0set= 0,reset= 1,q= x,qbar= x
#                    1set= 0,reset= 1,q= 0,qbar= x
#                    2set= 0,reset= 1,q= 0,qbar= 1
#                   10set= 0,reset= 0,q= 0,qbar= 1
#                   20set= 1,reset= 0,q= 0,qbar= 1
#                   21set= 1,reset= 0,q= 0,qbar= 0
#                   22set= 1,reset= 0,q= 1,qbar= 0
#                   30set= 1,reset= 1,q= 1,qbar= 0
#                   31set= 1,reset= 1,q= 0,qbar= 0

可以对照仿真输出来观察延迟输出的影响。初始reset为1，促使q变为0，所以经过1ns之后q从x变为0，此时qbar没有得到能改变输出的值，依然保持x，在2ns时通过set为0和q为0共同驱动qbar变为1，变化结束，后面的过程相似。

移位除法器模型

采用的算法类似笔算除法，只是变为了二进制而不是十进制。由于代码较长，采用层次化的方式进行设计，同时采用循环迭代的方式使用一个电路模板反复运算得到最后的结果。这个过程正好是流水线的一个反例，流水线牺牲了电路面积带来的速度的提升，而本例中的循环迭代反复使用同一个电路模板，节省了最后电路的面积，但是时间上也会相应延长。该除法器的顶层模块如下：

复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
module div2(clk, reset, start, A, B, D, R, ok, err);
	parameter n = 32;
	parameter m = 16;
	
	input clk, reset, start;
	input [n-1:0] A, B;
	output [n+m-1:0] D;
	output [n-1:0] R;
	output ok, err;
	
	wire invalid, carry, load, run;
	
	div_ctl UCTL(clk, reset, start, invalid, carry, load, run, err, ok);
	div_datapath UDATAPATH(clk, reset, A, B, load, run, invalid, carry, D, R);
	
endmodule

模块中包含两个子模块，div_ctl是用来生成控制信号的，div_datapath是用来进行迭代计算的，整体的模块划分如下图所示。
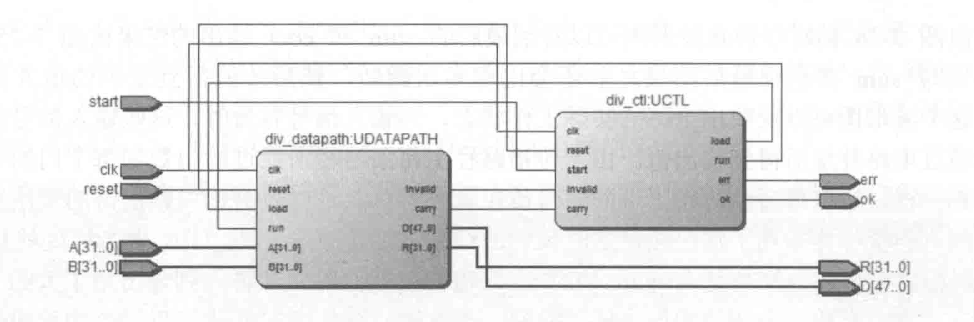
div2电路图
在两个模块中，div_ctl作为生成控制信号的单元是非常重要的，相当于整个电路的大脑，该模块的代码如下：

复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
module div_ctl(clk, reset, start, invalid, carry, load, run, err, ok);
	parameter n = 32;
	parameter m = 16;
	parameter STATE_INIT = 3'b001;
	parameter STATE_RUN = 3'b010;
	parameter STATE_FINISH = 3'b100;
	input clk, reset, start, invalid, carry;
	output load, run, err, ok;
	
	reg [2:0] current_state, next_state;
	reg [5:0] cnt;
	reg load, run, err, ok;
	
	always @(posedge clk or negedge reset)
	begin
		if(!reset) begin
			current_state <= STATE_INIT;
			cnt <= 0;
		end else begin
			current_state <= next_state;
			if(run) cnt <= cnt + 1'b1;
		end
	end
	
	always @(posedge clk or negedge reset)
	begin
		if(!reset) begin
			err <= 0;
		end else if(next_state==STATE_RUN) begin
			if(invalid) err <= 1;
		end
	end
	
	always @(current_state or start or invalid or carry or cnt)
	begin
		load <= 1'b0;
		ok <= 1'b0;
		run <= 1'b0;
			
		case(current_state)
			STATE_INIT:begin
				if(start) next_state <= STATE_RUN;
				else next_state <= STATE_INIT;
				load <= 1;
			end
			STATE_RUN : begin
				run <= 1;
				if(invalid) begin
					next_state <= STATE_FINISH;
				end else if(cnt==(n+m-1)) begin
					next_state <= STATE_FINISH;
				end else begin
					next_state <= STATE_RUN;
				end
			end
			STATE_FINISH : begin
				ok <= 1;
				next_state <= STATE_FINISH;
			end
			default : begin
				next_state <= STATE_INIT;
			end
		endcase
	end
endmodule

此模块的功能主要是根据当前的一些信号情况来判断电路应该处于哪个工作状态，根据不同的工作状态来输出不同的控制信号，采用的方式是时序电路设计中的核心方法：有限状态机。
当前的控制模板按下图所示状态进行工作，分为出事阶段、运行阶段和结束阶段，每个阶段能进行不同的信号控制。具体到每个阶段的功能，初始阶段完成数据的接受，运行阶段送入迭代单元进行迭代计算，接受阶段把计算所得的最终结果输出，此电路不能直接返回初始阶段，需要外界施加复位信号。
div_ctl电路图

该功能的实现是通过下图所示电路完成的，该电路由div_ctl模块综合之后生成。
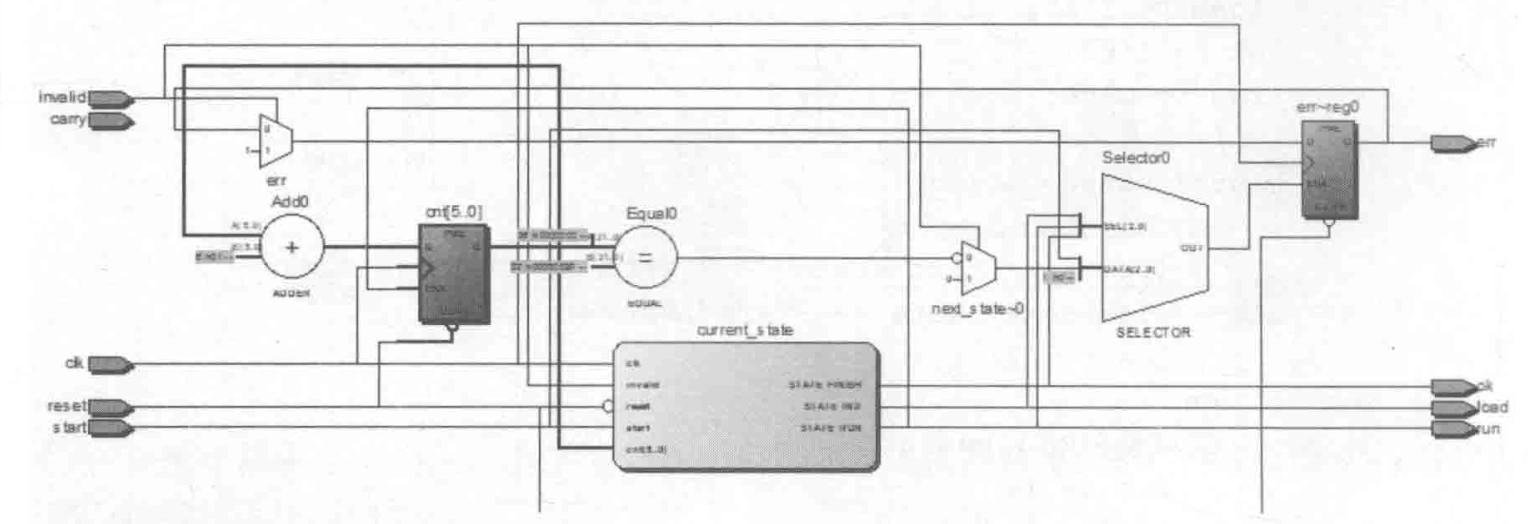
在这里插入图片描述
迭代电路div_datapath的模块代码如下

复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
module div_datapath(clk, reset, A, B, load, run, invalid, carry, D, R);
	parameter n = 32;
	parameter m = 16;
	input clk, reset;
	input [n-1:0] A, B;
	input load, run;
	output invalid, carry;
	output [n+m-1:0] D;
	output [n-1:0] R;
	
	reg [n+n+m-2:0] R0;
	reg [n+m-1:0] D;
	reg [n-1:0] B0;
	reg carry;
	
	wire invalid;
	wire [n-1:0] DIFF, R;
	wire CO;
	
	assign R = {carry, R0[n+n+m-2:n+m]};
	assign invalid = {B0==0};
	
	sub sub(R0[n+n+m-2:n+m-1], B0, 1'b0, DIFF, CO);	//实例化减法器
	
	always @(posedge clk)
	begin
		if(load) begin				//初始阶段
			D <= 0;
			R0 <= {{(n-1){1'b0}}, A, {m{1'b0}}};
			B0 <= B;
			carry <= 1'b0;
	end
		else if(run) begin			//结束阶段
			if(CO && !carry) begin
				R0 <= {R0, 1'b0};
				D <= {D[n+m-2:0], 1'b0};
				carry <= R0[n+n+m-2];
			end else begin			//迭代阶段
				R0 <= { DIFF, R0[n+m-2:0], 1'b0};
				D <= {D[n+m-2:0], 1'b1};
				carry <= DIFF[n-1];
			end
		end
	end
endmodule

该模块的主要部分在代码中已经注释出来，分别对应初始阶段、结束阶段和迭代阶段，在初始阶段接受数值并送入减法器，迭代阶段仿照笔算时的方式每次移动1位并送入减法器得到差值，如此循环直至最后剩余的值小于除数，此时表示运算已经完毕，也就是代码中的结束阶段。整个模块综合之后的电路图如下图所示。
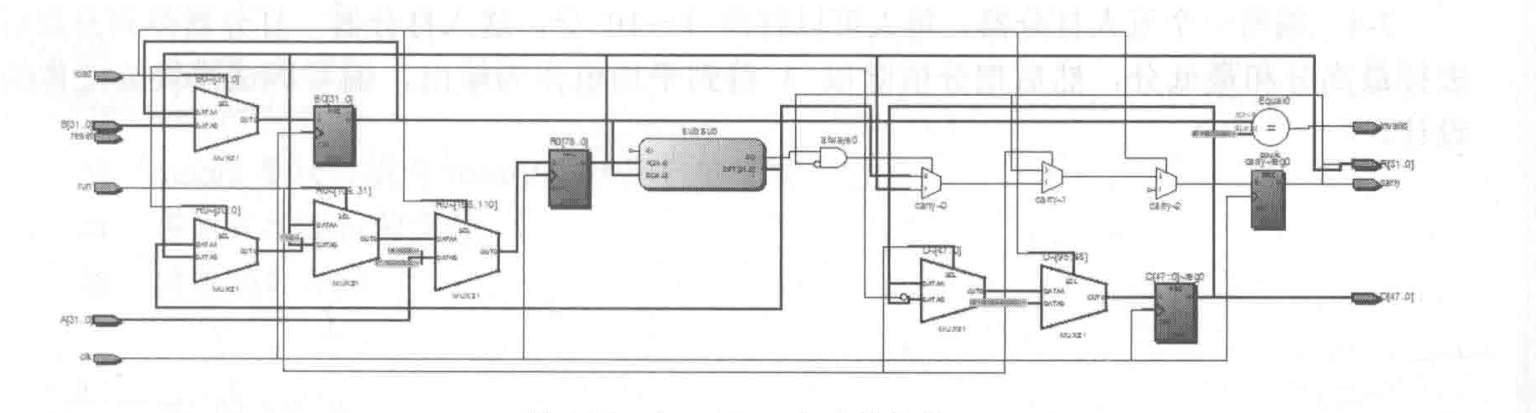
div_datapath电路图
这个模块中调用的减法器很简单，仿照加法器得到代码如下，所得电路如下图所示。

复制代码
1
2
3
4
5
6
7
8
9
10
11
module sub(A, B, CI, DIFF, CO);
	parameter n = 32;
	input [n-1:0] A, B;
	input CI;
	output [n-1:0] DIFF;
	output CO;
	
	assign {CO, DIFF} = {1'b0, A} - {1'b0, B} - {{n{1'b0}}, CI};
endmodule

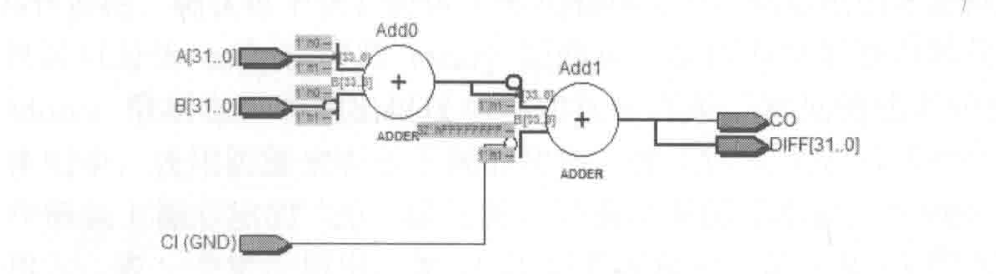
减法器结构

该div模块设计模块部分就结束了，其仿真模块如下。

复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
`timescale 1ns/10ps		//时间精度

module tb_div2;
	parameter n = 32;		//参数说明
	parameter m = 16;
	
	reg clk, reset;
	reg start;
	wire [n+m-1:0] D;
	wire [n-1:0] R;
	wire err, ok;
	integer i;			//内部变量声明
	
	reg [n-1:0] dividend;	//被除数
	reg [n-1:0] divisor;	//除数
	reg [n+m-1:0] quotient;	//参考商
	reg [n-1:0] remainder;    //参考余数
	
	div2 UDIV(clk, reset, start, dividend, divisor, D, R, ok, err);
		//实例化引用
	
	function [n+n+(n+m)+(n)-1:0] gen_rand_data;
		//函数部分，生成被除数、除数，和商与余数的参考值
	input integer i;
	reg [n+m-1:0] dividend;
	reg [n+m-1:0] divisor;
	reg [n+m-1:0] quotient;
	reg [n+m-1:0] remainder;
	integer k;
	integer flag;
	
	begin 
		k = {i/4 % 32 + 1};
		flag = 1;
		while(flag) 
		begin
		dividend = {{$random}, {m{1'b0}}};		//随机数生成被除数，并扩展位
		divisor = {{m{1'b0}}, {$random}};			//随机数生成除数，被扩展位
		
		divisor = divisor % (2 << k);
		if(divisor == {(n+m){1'b0}})
		begin
			$display("Divisor is zero!!!");
			end else begin
				flag = 0;
			end
			quotient = dividend / divisor;
			remainder = dividend % divisor;		//行为模型，得到参考的商和余数
			
			if(remainder > divisor)		//商大于余数时报错
			begin 
				$display("Bad remainder!!!");
				$stop;
			end
			
			if(quotient * divisor + remainder != dividend)	//结果不符时报错
			begin
				$display("bad values!!!");
				$stop;
			end
			end
			
			gen_rand_data = {dividend[n+m-1:m], divisor[n-1:0], quotient, remainder[n-1:0]};	
			//返回函数值
		end
	endfunction
	
	initial		//时钟信号
	begin
		clk=0;
		forever
			#10 clk=~clk;
	end
	
	initial
	begin
		reset = 0;
		start = 0;
	  for(i=1; i<=1000; i=i+1)			//生成1000个数
	  begin	
	    {dividend, divisor, quotient, remainder} = gen_rand_data(i);
													//调用函数返回4个值
		 @(posedge clk);					//等待时钟信号复位
		    reset = 0;
		 @(posedge clk);					//下一时钟开始运算
			reset = 1;
			start = 1;
		 @(posedge ok);					//等到ok上沿，即运算结束时
			if(quotient!=D || remainder!=R)		//若结果与参数值不符，报错
			begin
				$display("BAD RESULT!!!");
				$display("result:quotient=48'd%d,remainder=32'd%d",D,R);
				 $stop;
			end
	  end
	  
	  $stop;			//1000个数后结束仿真
	end
endmodule

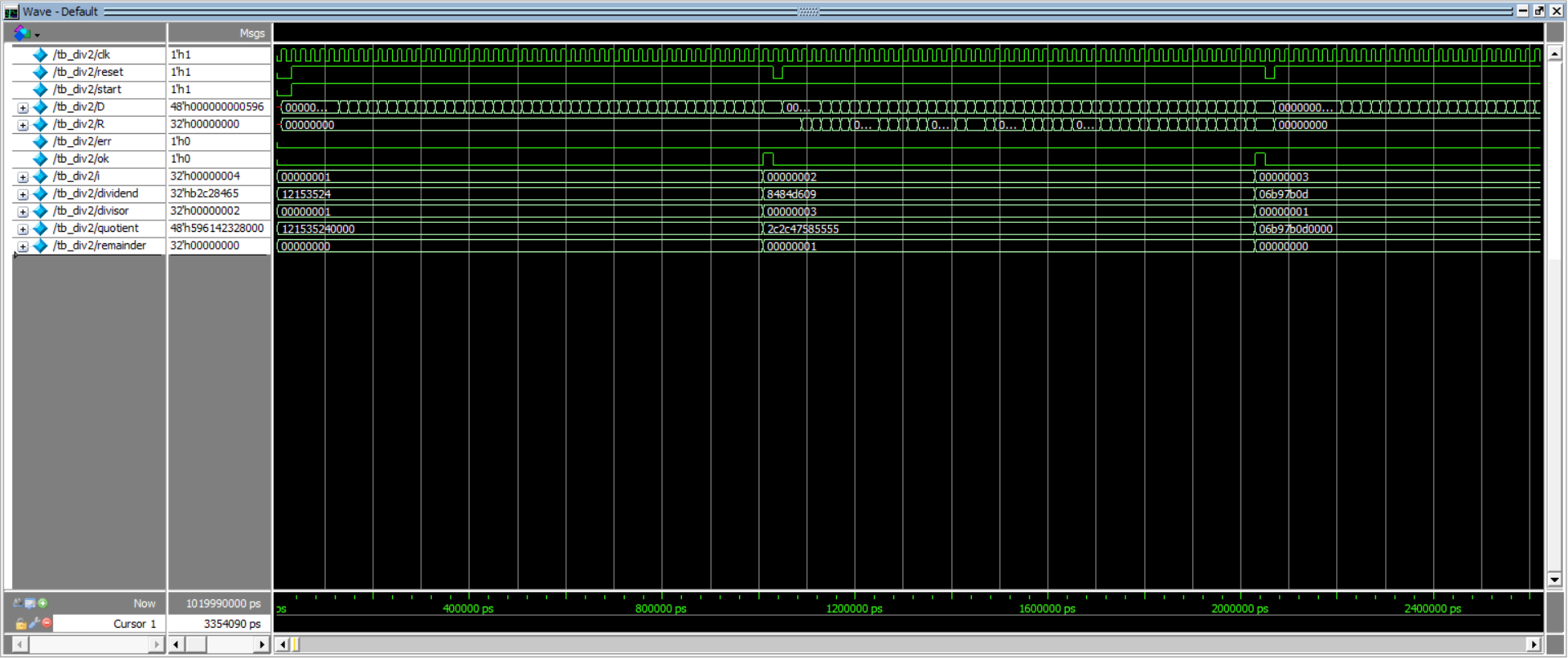
运行测试模块，一方面会根据行为模型生成参考输出值，另一方面有设计模块得到最好的实际输出，对比可知是否正确，如果出现结果不正确或是其他异常情况，使用显示任务进行报警。运行该测试模块进行仿真，得到的结果如下图所示。
div2仿真结果

实验视频地址：

bilibili

最后

以上就是醉熏小懒虫最近收集整理的关于独热码状态机，SR锁存器延迟模型，移位除法器模型的全部内容，更多相关独热码状态机内容请搜索靠谱客的其他文章。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
点赞(73)

相关文章

基于锁相环的直流电机控制系统simulink仿真一、理论基础二、部分MATLAB仿真
基于锁相环的直流电机控制系统simulink仿真一、理论基础二、部分MATLAB仿真
光电编码器原理及应用电路
光电编码器原理及应用电路
[转]使用D触发器制作正交编码器的鉴相电路
[转]使用D触发器制作正交编码器的鉴相电路
锁相环APLL仿真介绍
锁相环APLL仿真介绍
独热码状态机，SR锁存器延迟模型，移位除法器模型
独热码状态机，SR锁存器延迟模型，移位除法器模型
利用74LS161计数器芯片分别实现模12，模20的计数器，并在QuartusⅡ上进行仿真
利用74LS161计数器芯片分别实现模12，模20的计数器，并在QuartusⅡ上进行仿真
74HC163与74HC161 同步和异步计数器仿真示例
74HC163与74HC161 同步和异步计数器仿真示例
Java并发方面最为权威的人物:Doug Lea
Java并发方面最为权威的人物:Doug Lea

评论列表共有 0 条评论

立即
投稿
返回
顶部