【梳理】数字设计基础与应用 第3章 时序逻辑基础 3.4 移位寄存器

教材：数字设计基础与应用 第二版 邓元庆 关宇 贾鹏 石会 编著 清华大学出版社
源文档高清截图在后

3.4 移位寄存器

1、移位寄存器（shift register）是用于寄存二进制信息并将信息移位的时序逻辑电路，只能寄存二进制信息的称为寄存器。移位寄存器在数字通信中应用极其广泛。例如远程通信中，发送端将要发送的信息送入移位寄存器，然后信息被逐位移出到发送线路（称为数据格式的并入串出变换）；接收端从接收线路逐位接收信息并送入移位寄存器，接收完一个完整的数据组后才取走数据（串入并出变换）。寄存器和移位寄存器一般由D触发器构成。

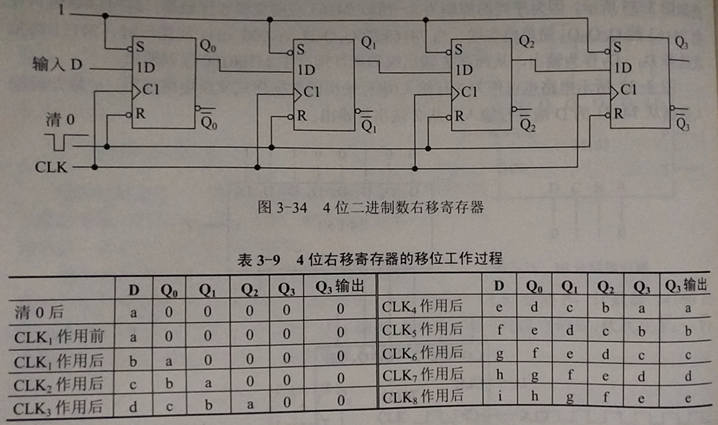
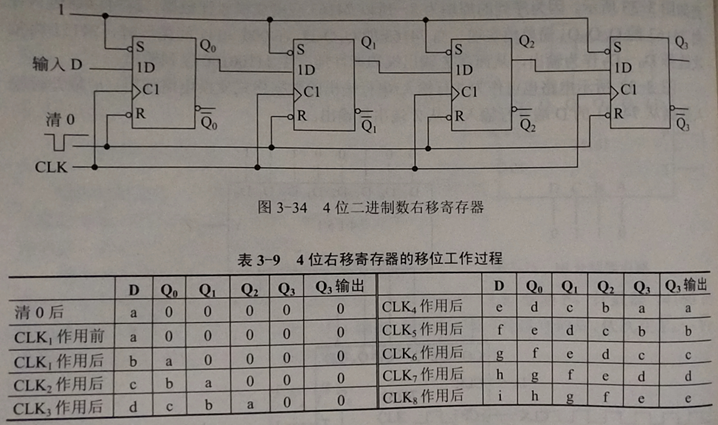
2、下图是用带异步置位、复位端的D触发器构成的4位右移寄存器。CLK的每个上升沿，数据右移一位，输入数据被移入Q0寄存。虽然各个D触发器几乎同时接收到上升沿，但触发器存在一定的延迟性，所以每次上升沿期间D只能移动一位。改变D端的连接方式，可以将其改成左移寄存器。

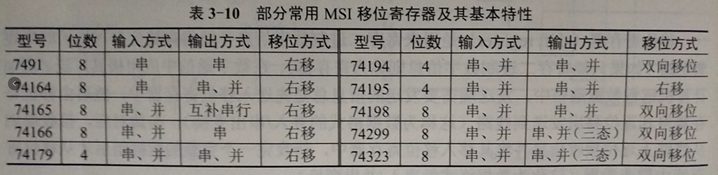
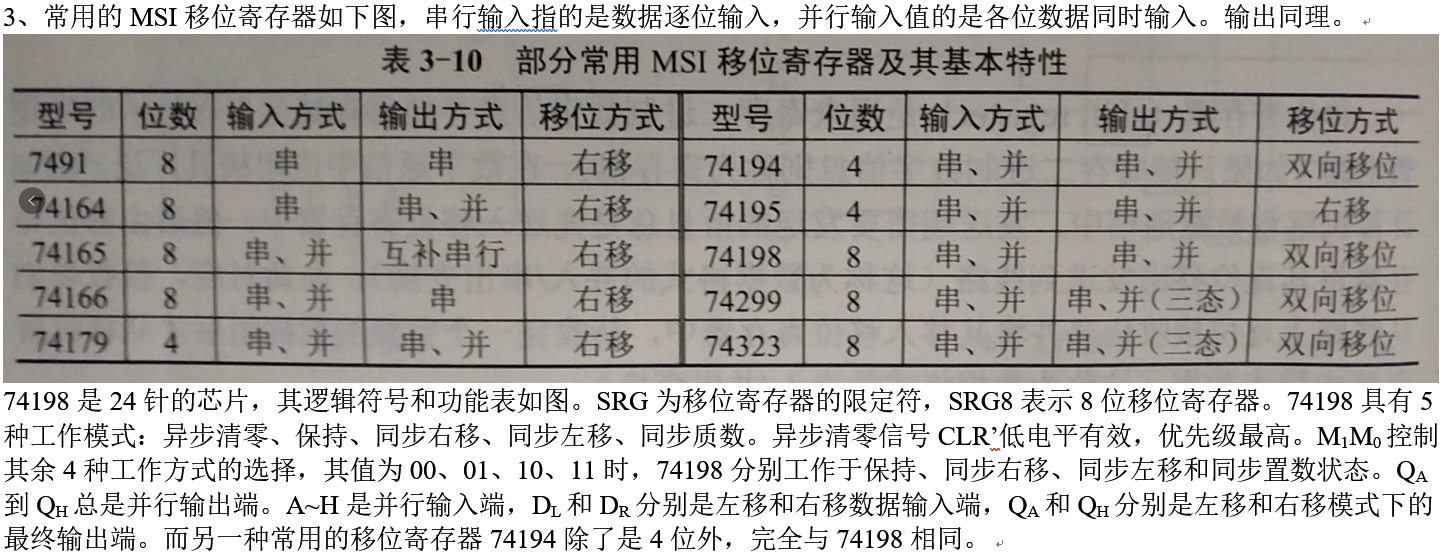
3、常用的MSI移位寄存器如下图，串行输入指的是数据逐位输入，并行输入值的是各位数据同时输入。输出同理。

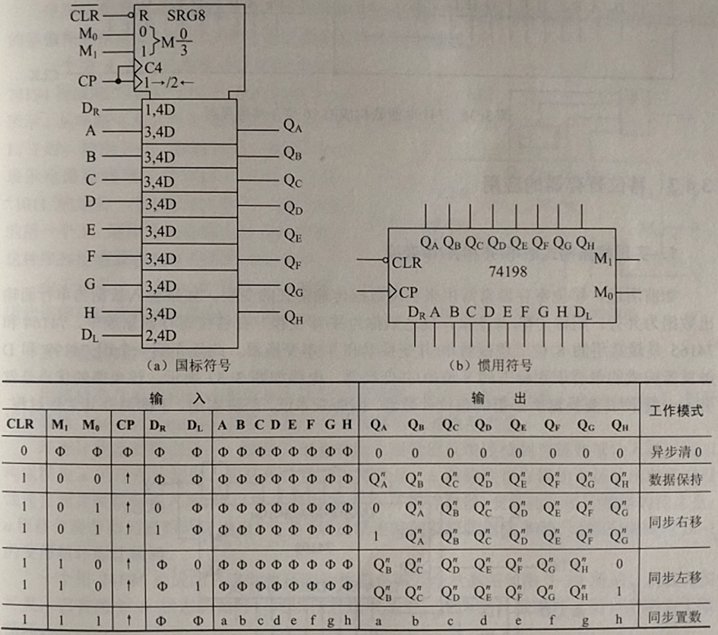
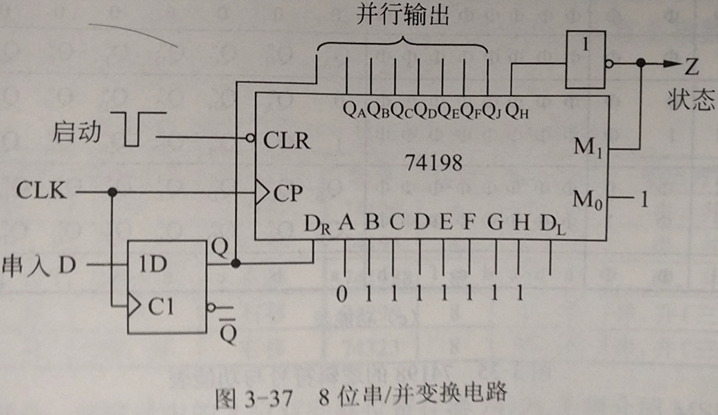
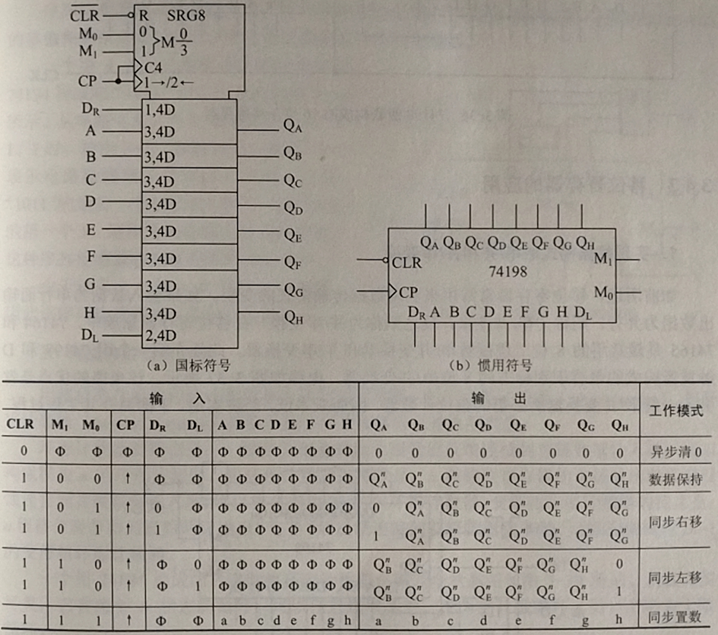
74198是24针的芯片，其逻辑符号和功能表如图。SRG为移位寄存器的限定符，SRG8表示8位移位寄存器。74198具有5种工作模式：异步清零、保持、同步右移、同步左移、同步质数。异步清零信号CLR’低电平有效，优先级最高。M1M0控制其余4种工作方式的选择，其值为00、01、10、11时，74198分别工作于保持、同步右移、同步左移和同步置数状态。QA到QH总是并行输出端。A~H是并行输入端，DL和DR分别是左移和右移数据输入端，QA和QH分别是左移和右移模式下的最终输出端。而另一种常用的移位寄存器74194除了是4位外，完全与74198相同。

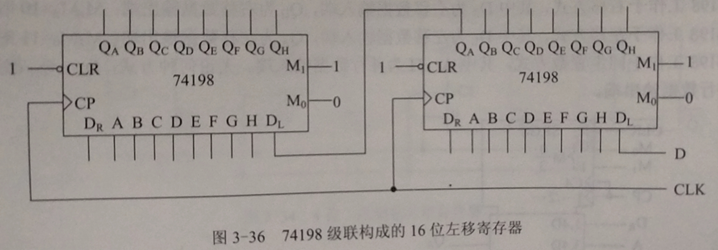
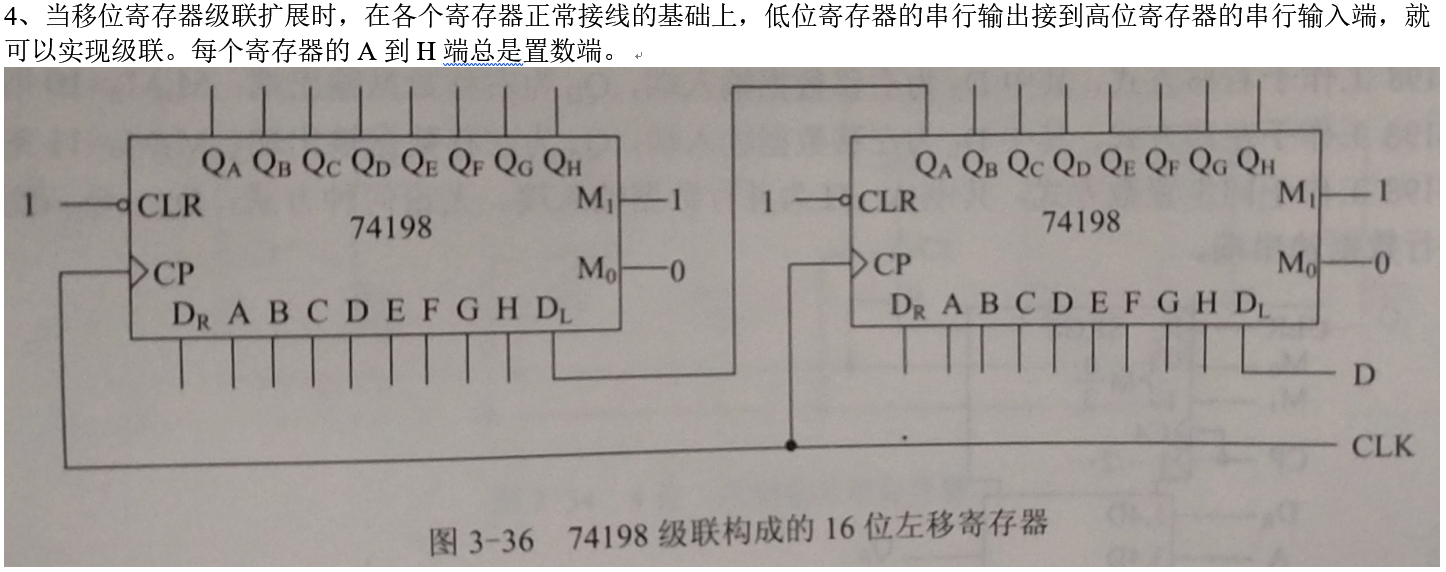
4、当移位寄存器级联扩展时，在各个寄存器正常接线的基础上，低位寄存器的串行输出接到高位寄存器的串行输入端，就可以实现级联。每个寄存器的A到H端总是置数端。

5、移位寄存器的应用：
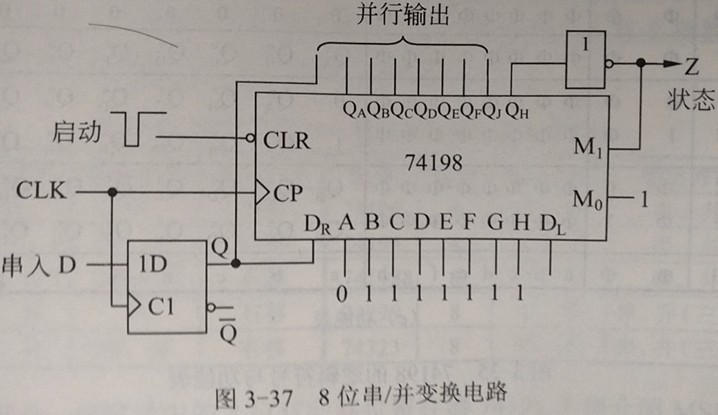
（1）实现数据的串并转换（并串转换）。
以74198为例，接线方式如下图。开始时先令CLR’ = 0将已有数据清零，然后A~H分别接01111111，再令M1M0 = 11，D = D0（最低位数据），给一个脉冲上沿，将01111111置入74198，同时最低位数据D0进入触发器。再给7个脉冲，前7位数据D0到D6，最高位D7则通过一个额外的D触发器的Q端直接输出。此时先前置数的0已经移到了QH，经过非门后输出Z = 1。该信号给出后，表示8位串行数据已经全部变换为并行数据，应当取走。而Z端与M1相连，又令M1M0 = 11，回到置数方式，开始下一轮转换。

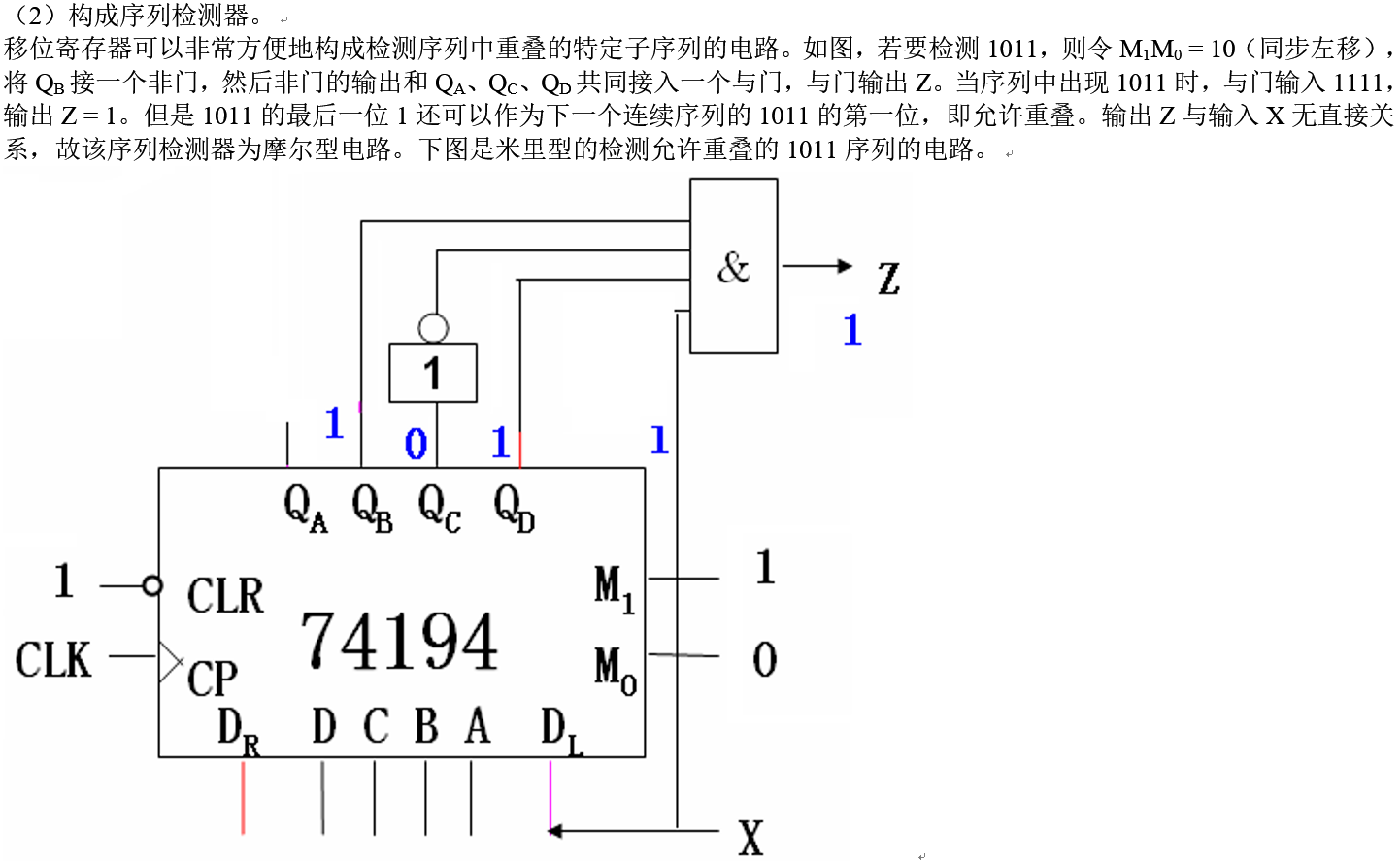
（2）构成序列检测器。
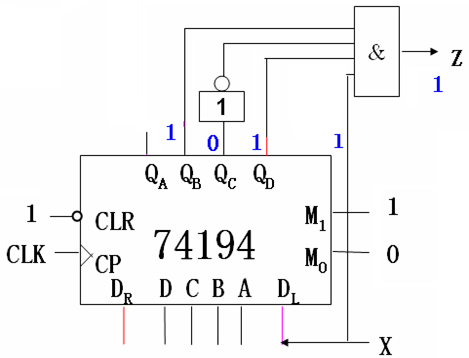
移位寄存器可以非常方便地构成检测序列中重叠的特定子序列的电路。如图，若要检测1011，则令M1M0 = 10（同步左移），将QB接一个非门，然后非门的输出和QA、QC、QD共同接入一个与门，与门输出Z。当序列中出现1011时，与门输入1111，输出Z = 1。但是1011的最后一位1还可以作为下一个连续序列的1011的第一位，即允许重叠。输出Z与输入X无直接关系，故该序列检测器为摩尔型电路。下图是米里型的检测允许重叠的1011序列的电路。

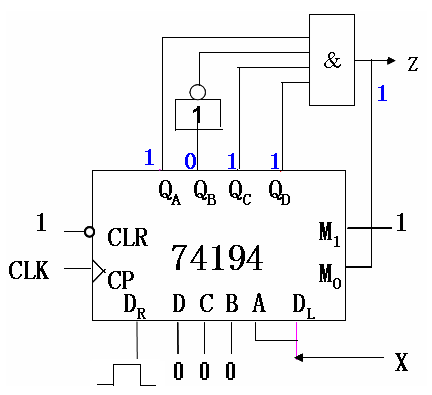
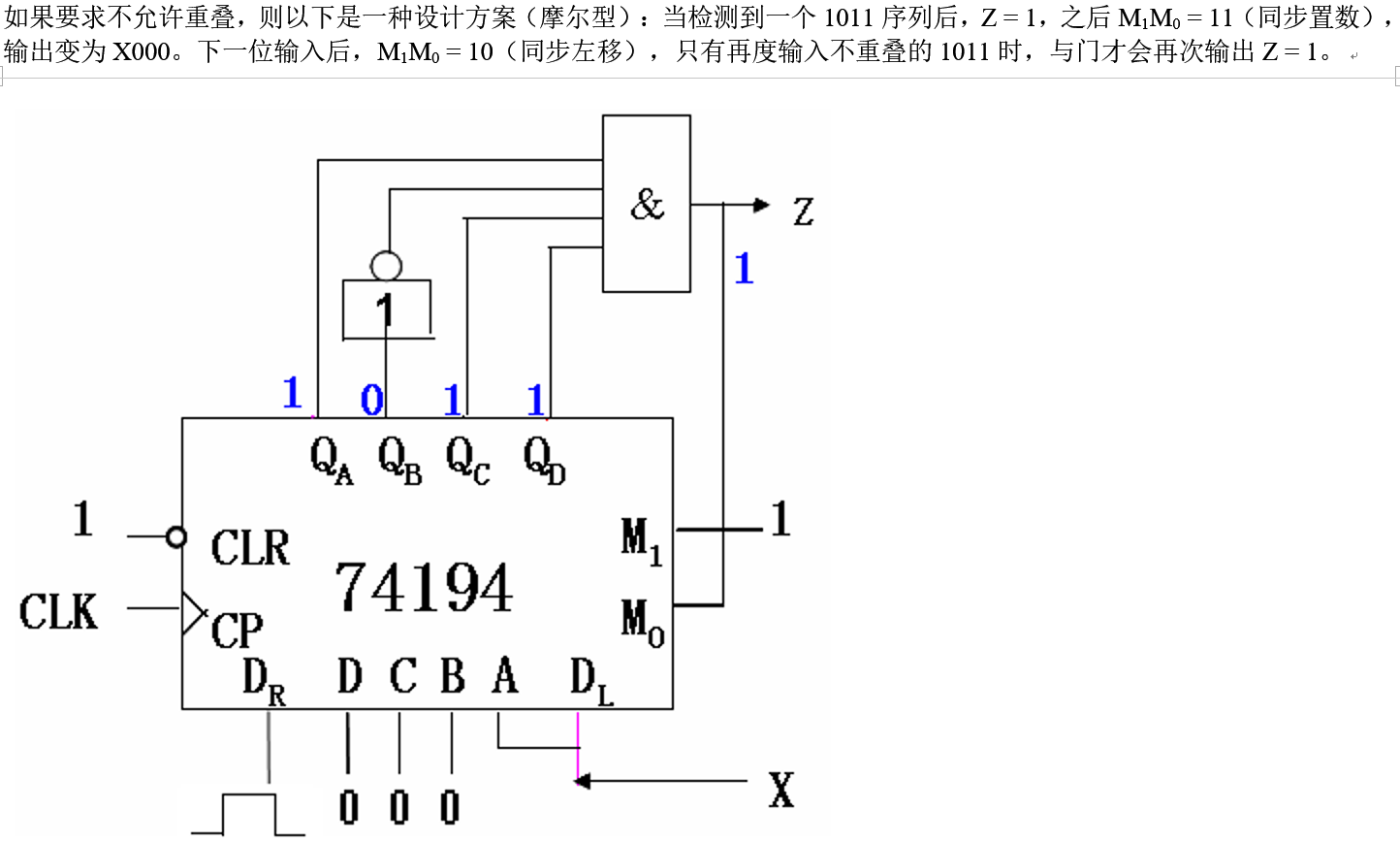
如果要求不允许重叠，则以下是一种设计方案（摩尔型）：当检测到一个1011序列后，Z = 1，之后M1M0 = 11（同步置数），输出变为X000。下一位输入后，M1M0 = 10（同步左移），只有再度输入不重叠的1011时，与门才会再次输出Z = 1。

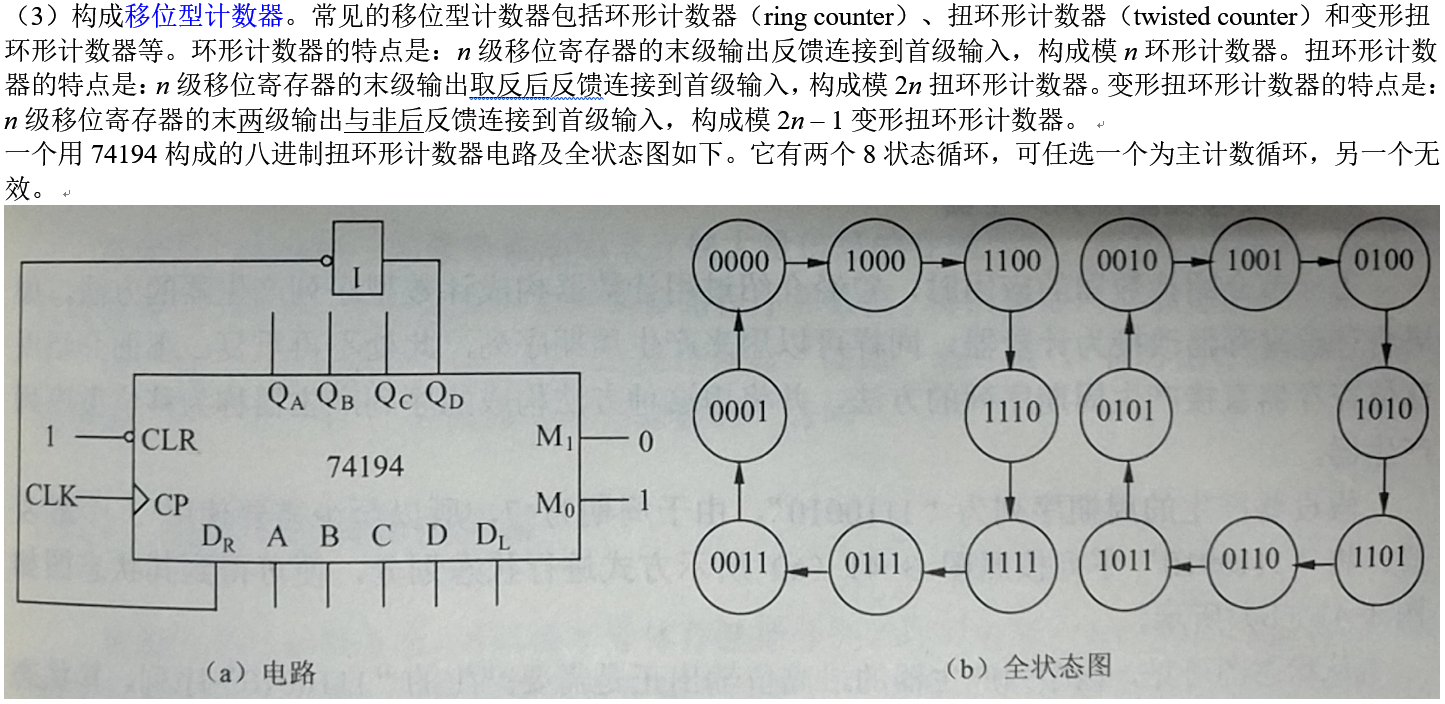
（3）构成移位型计数器。常见的移位型计数器包括环形计数器（ring counter）、扭环形计数器（twisted counter）和变形扭环形计数器等。环形计数器的特点是：n级移位寄存器的末级输出反馈连接到首级输入，构成模n环形计数器。扭环形计数器的特点是：n级移位寄存器的末级输出取反后反馈连接到首级输入，构成模2n扭环形计数器。变形扭环形计数器的特点是：n级移位寄存器的末两级输出与非后反馈连接到首级输入，构成模2n – 1变形扭环形计数器。
一个用74194构成的八进制扭环形计数器电路及全状态图如下。它有两个8状态循环，可任选一个为主计数循环，另一个无效。

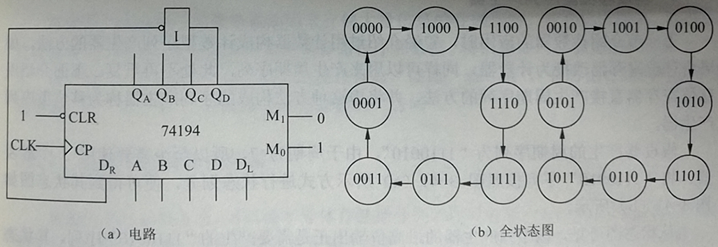
在时序电路中，常常要求电路具有自启动特性，即加电后无论处于什么状态，都要在有限个时钟内自动进入主循环，从而不必手动预置初始状态。自启动电路在工作过程如遇干扰而脱离主循环，也能在有限个周期内自动回归主循环，使得电路具有一定的纠偏能力。上图的电路中，当进入0000状态后，非门将1输入右移输入端，在下一个上升沿到来后，从1100开始继续。当进入1111状态后，非门将0输入右移输入端，在下一个上升沿到来后，从0111开始继续。这就是该电路的一个主循环。要使电路进入左侧的循环，必须手动设置这个循环中的8个状态对应的二进制值中的任意一个，再开始计数。对右侧循环同理，不再详细解释。显然，这个电路不具有自启动能力。一旦电路意外脱离了要求的计数循环，就无法自动回归。
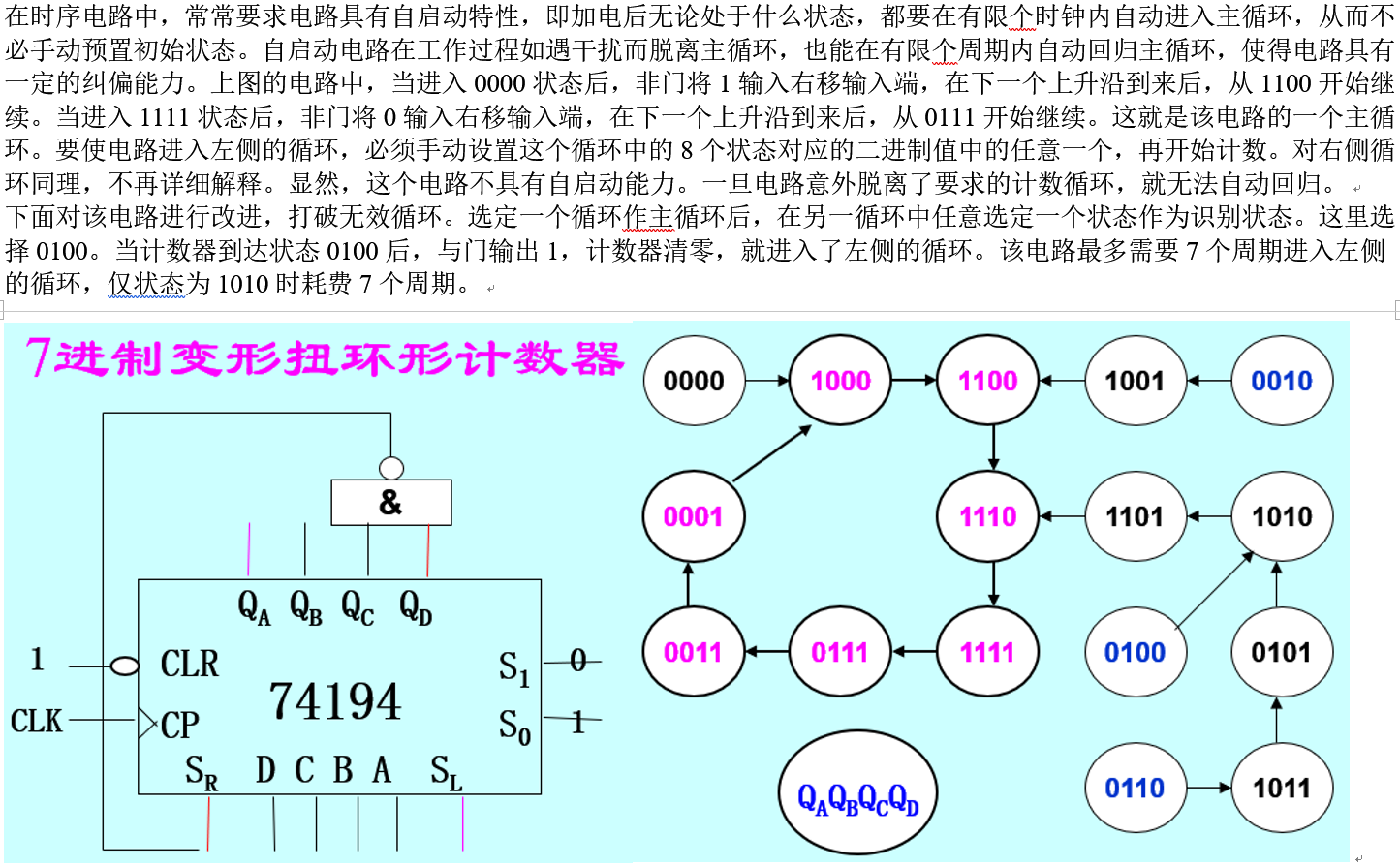
下面对该电路进行改进，打破无效循环。选定一个循环作主循环后，在另一循环中任意选定一个状态作为识别状态。这里选择0100。当计数器到达状态0100后，与门输出1，计数器清零，就进入了左侧的循环。该电路最多需要7个周期进入左侧的循环，仅状态为1010时耗费7个周期。

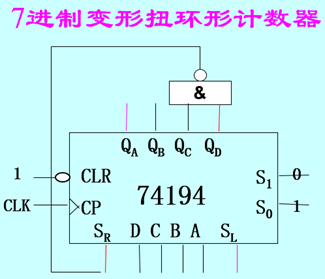
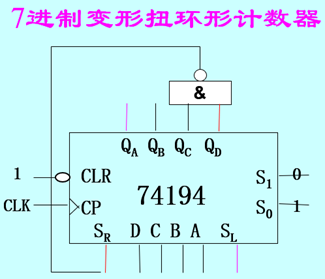
上图是一个由4位移位寄存器构成的7进制变形扭环形计数器及其状态图。如果选定1000→0001这7个状态构成的循环为主循环，当计数器的状态为0000时，与非门将1输入右移输入端，下一个状态是1000。类似地，当不在主循环中时，随着数据的右移，与非门的两个输入总会不同时为1，从而将1输入右移输入端。当与非门的两个输入均为1时，会将0输入右移输入端。可见，状态不处于主循环时无论在哪个状态，均可以在有限个周期内进入主循环。
除了串行加法器、串行比较器这类要求加点后必须具有特定初始状态的电路之外，以移位型计数器为代表的许多电路在采用这些方法进行处理后无需预置初始状态。
移位型计数器还有两个不足之处：状态编码比较乱，不利于采用现成的器件译码；有效利用的状态数量少，造成了资源浪费。这些因素限制了移位型计数器的使用。
（4）构成移位型序列产生器。
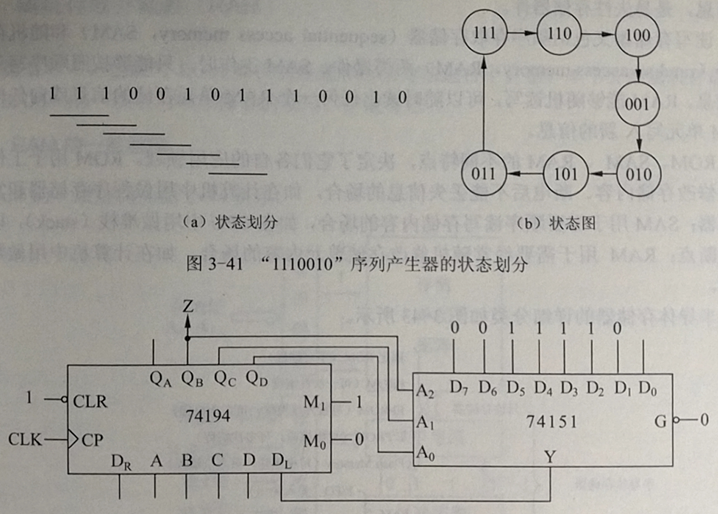
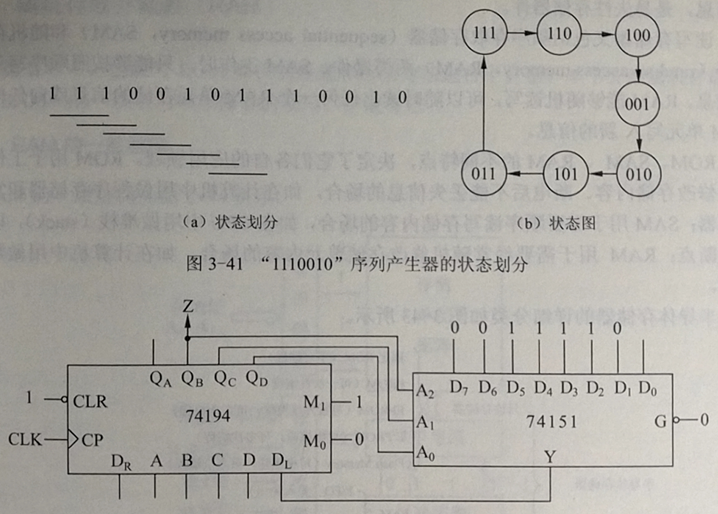
计数器可以构成计数型序列产生器。如果将移位寄存器改接成计数器，同样能产生周期序列。移位寄存器也可以直接产生周期序列。例如，设要产生周期序列1110010，周期为7。所以，至少需要使用三个触发器。由于是通过移位寄存器构造周期序列的，移位寄存器每次只能移动一位数据，所以可以得到如下的状态划分和状态图。由状态图，该序列产生器的最高位输出正好与序列匹配。其状态图可以靠左移位来完成。如果用74194实现，其左移串行数据输入DL可以用八选一数据选择器74151直接产生，电路如下图。QB端作为最高位输出Z。开始时，需要先对移位寄存器置数0111，Z输出1，QB、QC、QD将111送入数据选择器的地址位，Y输出0到DL。以此类推，状态对应的数据选择器的数据位的值是下一个状态的最低位的值，也是状态对应的划分的末位的下一位的值。每次把这个值压入移位寄存器进行左移，QB输出对应划分的首位。
该序列产生器使用了3个触发器，序列周期为7。n个触发器构成的周期为m＝2n – 1的移位型序列产生器称为最长周期序列产生器，简称m序列产生器。其反馈函数（反馈输入）可以表示为移位寄存器的某些Q端输出的异或函数，称为线性反馈。由电路图得，本电路中的反馈函数DL = QB^QC，因此74151也可以用一个异或门代替。
如果出现意外，导致移位寄存器输出0000，那么当D0为0时电路不能自启动，只有令D0 = 1，才会将一个1压入移位寄存器，从而进入主循环。
m序列具有非常好的伪随机特性，在数字通信中常常用于模拟白噪，评估系统的抗白噪声性能。

最后

以上就是风趣马里奥为你收集整理的【梳理】数字设计基础与应用 第3章 时序逻辑基础 3.4 移位寄存器的全部内容，希望文章能够帮你解决【梳理】数字设计基础与应用 第3章 时序逻辑基础 3.4 移位寄存器所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。