CDMA向量内积的计算

CDMA向量内积的计算

在平面坐标上，有A点和B点，A点坐标是$(x_1,y_1)$，B点坐标是$(x_2,y_2)$。

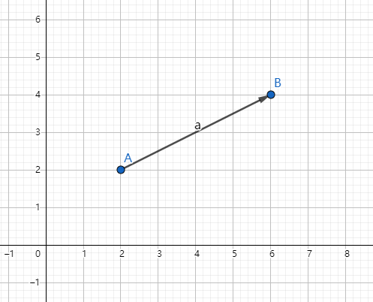
则
$$\overrightarrow{AB}=(x_2-x_1,y_2-y_1)$$
　　那么$\overrightarrow{AB}$向量的模是
　　$$\left|AB\right|=\sqrt{(x_2-x_1{)}^2+(y_2-y_1{)}^2}$$
即是线段AB的长度。
　　若A点在原点，即$x_1=0$，$y_1=0$，则$\overrightarrow{AB}=(x_2,y_2)$，如图2所示。

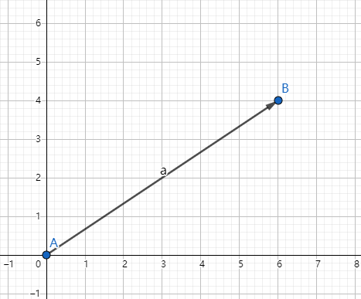
三维空间的向量就是在三维空间的两个点之间的带有方向和大小的量。在三维空间中有A和B点两，A点坐标是$(x_1,y_1,z_1)$，B点坐标是$(x_2,y_2,z_2)$。则
$$\overrightarrow{AB}=(x_2-x_1,y_2-y_1,z_2-z_1)$$
其他同理。
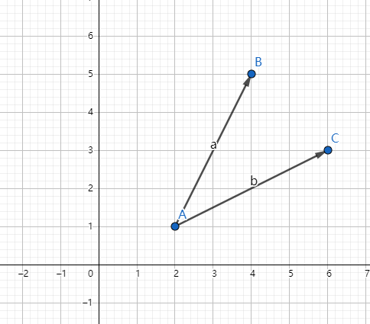
　　如图3所示，在二维平面上有两个向量$\overrightarrow{ａ}=(a_1,a_2)$，$\vec{b}=(b_1,b_2)$，则内积$$\overrightarrow{ａ}\cdot \vec{b}=\left|\overrightarrow{ａ}\right|\left|\vec{b}\right|\cos \theta (1)$$

若$\overrightarrow{ａ}$，$\vec{b}$垂直，则$\cos \theta =1$则
$$\overrightarrow{ａ}\cdot \vec{b}=\left|\overrightarrow{ａ}\right|\left|\vec{b}\right|\cos \theta =\left|\overrightarrow{ａ}\right|\left|\vec{b}\right|(2)$$
由(1)式可得
$$\overrightarrow{ａ}\cdot \vec{b}=a_1{b}_1+a_2{b}_2(3)$$

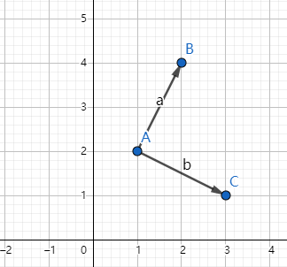
例1

如图4所示，图中有两个向量$\overrightarrow{ａ}$与$\vec{b}$，A，B，C三点的坐标分别为A(1,2)，B(2,4)，C(3,1)。则
$$\overrightarrow{ａ}=(a_1,a_2)=(2-1,4-2)=(1,2)$$
$$\vec{b}=(b_1,b_2)=(3-1,1-2)=(2,-1)$$
所以
$$\overrightarrow{ａ}\cdot \vec{b}=a_1{b}_1+a_2{b}_2=(1\times 2+2\times (-1))=0$$
因此，向量$\vec{a}$和$\vec{b}$正交，且两向量垂直。
规格化内积
$$\overrightarrow{ａ}\cdot \vec{b}=\frac{1}{2}(a_1{b}_1+a_2{b}_2)$$
而规格化内积
$$\overrightarrow{ａ}\cdot \vec{a}=\frac{1}{2}(a_1{a}_1+a_2{a}_2)=\frac{1}{2}(1\times 1+2\times 2)=2.5\ne 1$$
假设码片向量是2维的，这个2维的向量是不能作为发送站的码片向量的。

当两个m维向量有两个向量$\overrightarrow{ａ}=(a_1,a_2,\cdots a_m)$，$\vec{b}=(b_1,b_2,\cdots b_m)$，则规格化内积为
$$\overrightarrow{ａ}\cdot \vec{b}=\frac{1}{m}\sum _{i=0}^m{a}_i{b}_i=\frac{1}{m}(a_1{b}_1+a_2{b}_2+\cdots +a_m{b}_m)(4)$$

例2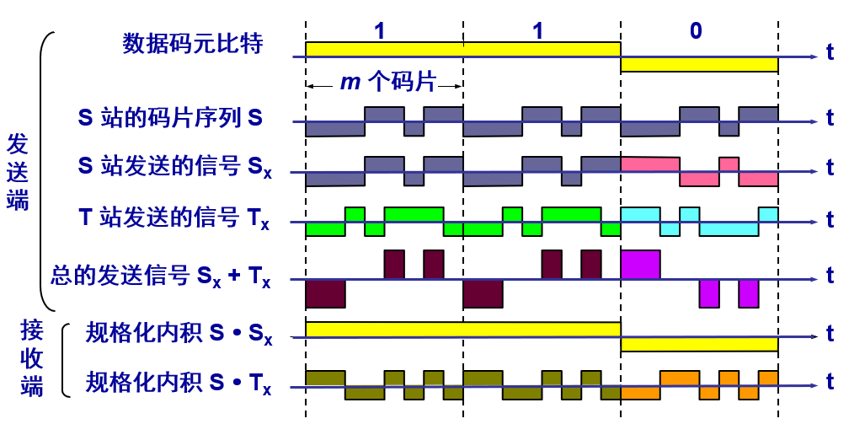

S站的码片序列S是（-1 -1 -1 +1 +1 -1 +1 +1）
T站的码片序列T是（-1 -1 +1 -1 +1 +1 +1 -1）
当数据码元比特为1时，发送信号$S_x+T_x$是（-2 -2 0 0 2 0 2 0）
因为$$\overrightarrow{S}\cdot (\overrightarrow{S_x}+\overrightarrow{T_x})=\overrightarrow{S}\cdot \overrightarrow{S_x}+\overrightarrow{S}\cdot \overrightarrow{T_x}$$
且规格化内积
$\overrightarrow{S}\cdot \overrightarrow{S_x}=\frac{1}{8}[(-1)\times (-1)+(-1)\times (-1)+(-1)\times (-1)+(+1)\times (+1)+(+1)\times (+1)+(-1)\times (-1)+(+1)\times (+1)+(+1)\times (+1)]=1$
规格化内积
$\overrightarrow{S}\cdot \overrightarrow{T_x}=\frac{1}{8}[(-1)\times (-1)+(-1)\times (-1)+(-1)\times (+1)+(+1)\times (-1)+(+1)\times (+1)+(-1)\times (+1)+(+1)\times (+1)+(+1)\times (-1)]=0$
所以
$$\overrightarrow{S}\cdot (\overrightarrow{S_x}+\overrightarrow{T_x})=\overrightarrow{S}\cdot \overrightarrow{S_x}+\overrightarrow{S}\cdot \overrightarrow{T_x}=1+0=1$$
所以S站发出的数据码元为1。
若计算的结果为-1，则说明S站发出的数据码元为0，若计算结果为0，则说明S站没有发送数据。

例3

最后

以上就是慈祥西牛为你收集整理的CDMA向量内积的计算的全部内容，希望文章能够帮你解决CDMA向量内积的计算所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。