第 4 章 信道
文章目录
- 第 4 章 信道
- 引言
- 4.1 无线信道
- 4.2 有线信道
- 4.3 信道数学模型
- 4.3.1 调制信道模型
- 4.4 恒参/随参信道特性对信号传输的影响
- 4.5 信道噪声
- 4.6 信道容量
- 4.6.2 连续信道容量
引言
-
信道的定义
信道是信号的传输媒质(狭义信道)
它可分为有线信道与无线信道两类

信道除包括传输媒质外,还包括有关的变换装置(如:发送设备、接收设备、馈线与天线、调制器、解调器等等)。称这种扩大范围的信道为广义信道
在讨论通信的一般原理时,我们采用广义信道
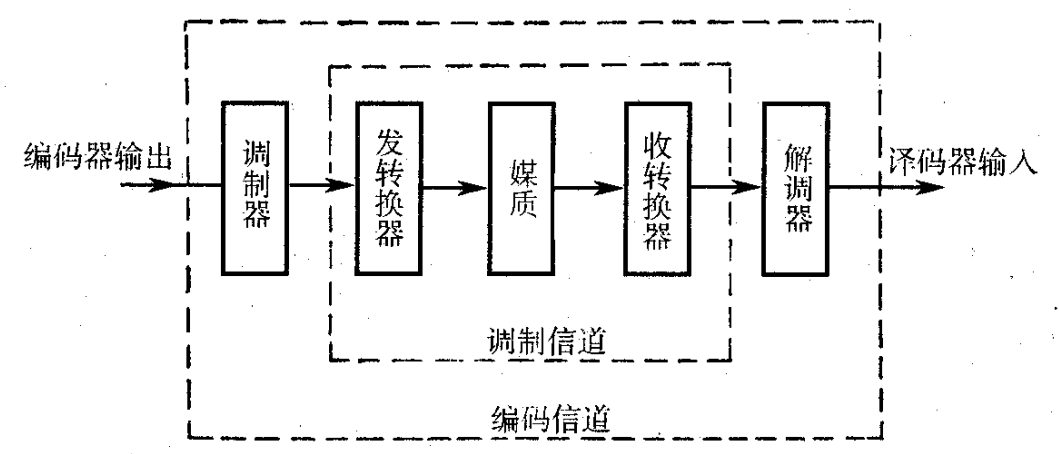
广义信道按照功能,划分为调制信道与编码信道
- 调制信道是指调制器输出端到解调器输入端的部分
- 在数字通信系统中,编码信道是指编码器输出端到译码器输入端的部分
-
概述
- 狭义信道:——传输媒质
- 有线信道:明线、电缆、光纤
- 无线信道:自由空间或大气层
- 广义信道:
- 调制信道:研究调制/解调问题
- 编码信道:研究编码/译码问题
- 狭义信道:——传输媒质
4.1 无线信道
-
无线电波波长与频率
λ f = c Δ f = c Δ λ λ 2 lambda f=c\ Delta f=frac{cDeltalambda}{lambda^2} λf=cΔf=λ2cΔλ
波段越高,数据传输率越高 -
视线传播
h = D 2 8 r ≈ D 2 50 ( m ) h=frac{D^2}{8r}thickapprox frac{D^2}{50}(m) h=8rD2≈50D2(m)
D 为收发天线间距离(km)
4.2 有线信道
-
光纤传输系统组成
-
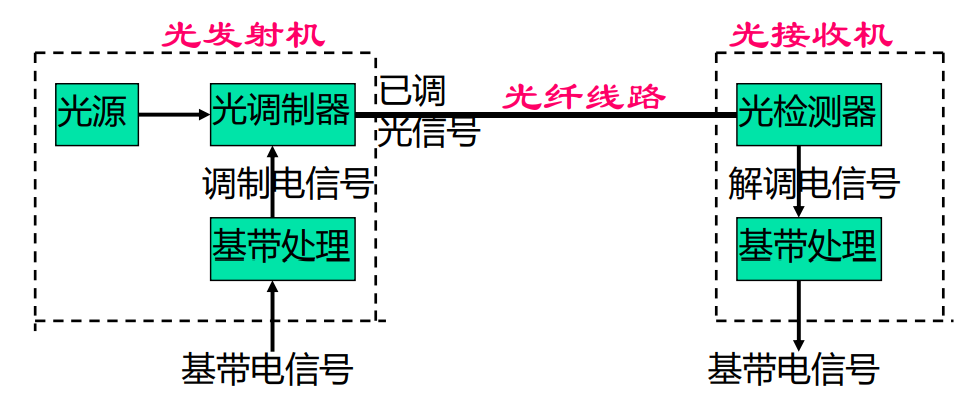
光纤通信:以光导纤维(光纤)为传输媒质,以光波为载波,实现信息传输
-
光纤传输系统的基本组成
-
4.3 信道数学模型
4.3.1 调制信道模型
-
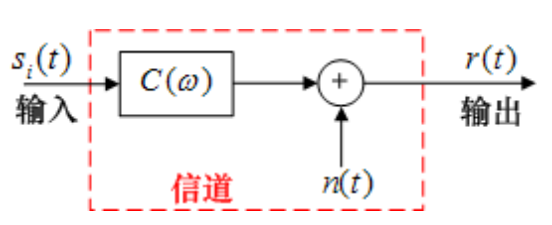
模型:叠加有噪声的线性时变/时不变网络:
-
共性:
- 有一对(或多对)输入端和输出端
- 大多数信道都满足线性叠加原理
- 对信号有固定或时变的延迟和损耗
- 无信号输入时,仍可能有输出(噪声)
-
入出关系:
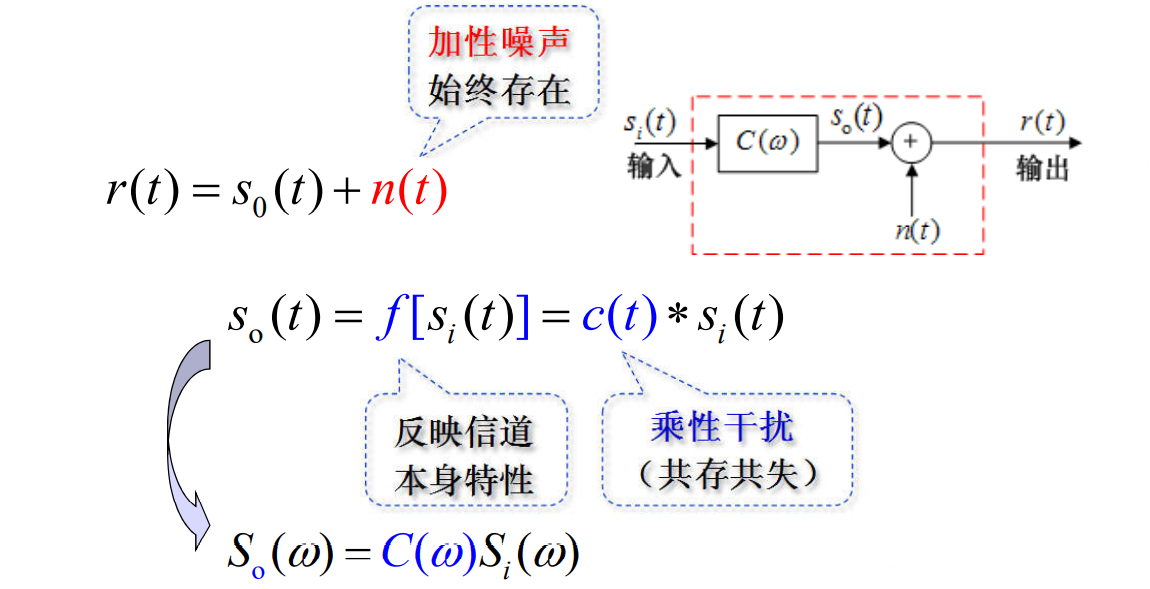
- 调制信道对信号的影响程度取决 C ( ω ) C(omega) C(ω) 与 n ( t ) n(t) n(t) 的特性
- 不同的物理信道具有不同的特性 C ( ω ) = C(omega)= C(ω)= 常数(可取1)
调制信道分为:(根据信道的时变特性)
- 恒参信道——特性基本不随时间变化
- 随参信道——特性随时间随机快变化
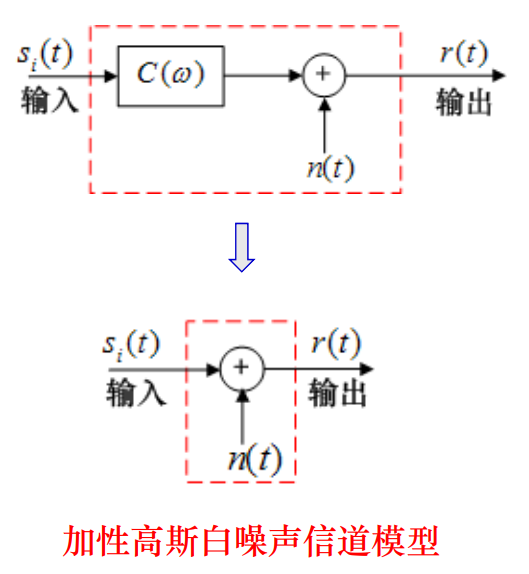
-
调制信道模型
e 0 ( t ) = f [ e i ( t ) ] + n ( t ) e_0(t)=f[e_i(t)]+n(t) e0(t)=f[ei(t)]+n(t)
式中
e i ( t ) — — 信 道 输 入 端 信 号 电 压 ; e o ( t ) — — 信 道 输 出 端 信 号 电 压 ; n ( t ) — — 噪 声 电 压 e_i(t)——信道输入端信号电压;\ e_o(t)——信道输出端信号电压;\ n(t)——噪声电压 ei(t)——信道输入端信号电压;eo(t)——信道输出端信号电压;n(t)——噪声电压
通常假设: f [ e i ( t ) ] = k ( t ) e i ( t ) f[e_i(t)]=k(t)e_i(t) f[ei(t)]=k(t)ei(t)这时上式变为:
e o ( t ) = k ( t ) e i ( t ) + n ( t ) — — 信 道 数 学 模 型 e_o(t)=k(t)e_i(t)+n(t)——信道数学模型 eo(t)=k(t)ei(t)+n(t)——信道数学模型- 因 k(t) 随 t 变,故信道称为时变信道
- 因 k(t) 与 e i ( t ) e_i(t) ei(t) 相乘,故称其为乘性干扰
- 因 k ( t ) k(t) k(t) 作随机变化,故又称信道为随参信道
- 若 k(t) 变化很慢或很小,则称信道为恒参信道
- 乘性干扰特点:当没有信号时,没有乘性干扰
4.4 恒参/随参信道特性对信号传输的影响
-
恒参信道特性及其对信号传输的影响
- 特点:传输特性随时间缓变或不变
- 举例:各种有线信道、卫星信道…
-
传输特性
H ( ω ) = ∣ H ( ω ) ∣ e j Φ ( ω ) { ∣ H ( ω ) ∣ ∼ ω 幅 频 特 性 ϕ ( ω ) ∼ ω 相 频 特 性 H(omega)=|H(omega)|e^{jPhi(omega)} begin{cases} |H(omega)|simomega 幅频特性\ phi(omega)simomega 相频特性 end{cases} H(ω)=∣H(ω)∣ejΦ(ω){∣H(ω)∣∼ω幅频特性ϕ(ω)∼ω相频特性 -
无失真传输
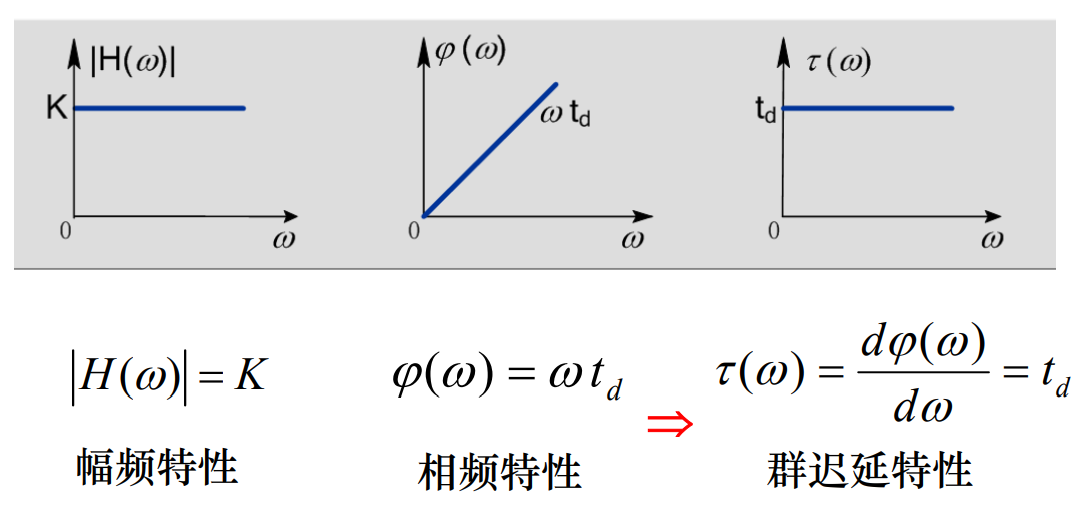
H ( ω ) = K e − j ω t d { ∣ H ( ω ) ∣ = K φ ( ω ) = ω t d H(omega)=Ke^{-jomega t_d} begin{cases} |H(omega)|=K\ varphi(omega)=omega t_d end{cases} H(ω)=Ke−jωtd{∣H(ω)∣=Kφ(ω)=ωtd-
无失真传输(理想恒参信道)特性曲线:
-
理想恒参信道的冲激响应:
H ( ω ) = K e − j ω t d ⇔ h ( t ) = K δ ( t − t d ) H(omega)=Ke^{-jomega t_d}Leftrightarrow h(t)=Kdelta(t-t_d) H(ω)=Ke−jωtd⇔h(t)=Kδ(t−td)
若输入信号为 s(t),则理想恒参信道的输出: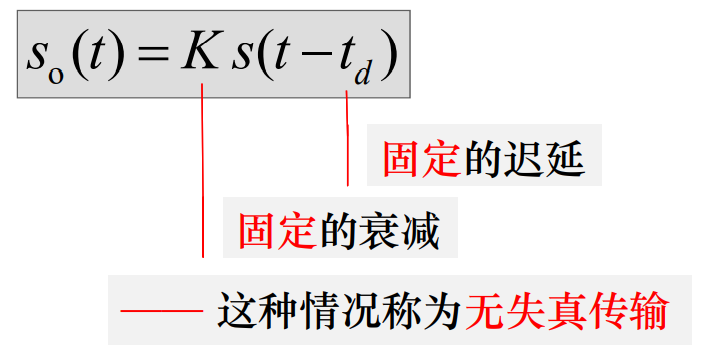
-
-
失真 影响 措施
-
幅频失真: ∣ H ( ω ) ∣ ≠ K |H(omega)|neq K ∣H(ω)∣=K
影 响 { 对 模 拟 信 号 : 造 成 波 形 失 真 → 信 噪 比 下 降 对 数 字 信 号 : 产 生 码 间 串 扰 → 误 码 率 增 大 影响 begin{cases} 对模拟信号:造成波形失真rightarrow信噪比下降\ 对数字信号:产生码间串扰rightarrow误码率增大 end{cases} 影响{对模拟信号:造成波形失真→信噪比下降对数字信号:产生码间串扰→误码率增大 -
相频失真: ϕ ( ω ) ≠ ω t d phi(omega)neqomega t_d ϕ(ω)=ωtd
群迟延失真: τ ( ω ) ≠ t d tau(omega)neq t_d τ(ω)=td
影 响 { 对 语 音 信 号 影 响 不 大 , 对 视 频 信 号 影 响 大 对 数 字 信 号 : 码 间 串 扰 → 误 码 率 增 大 影响 begin{cases} 对语音信号影响不大,对视频信号影响大\ 对数字信号:码间串扰rightarrow 误码率增大 end{cases} 影响{对语音信号影响不大,对视频信号影响大对数字信号:码间串扰→误码率增大
-
-
随参信道特性及其对信号传输的影响
-
随参信道举例
- 陆地移动信道
- 短波电离层反射信道
- 超短波流星余迹散射信道
- 超短波及微波对流层散射信道
- 超短波电离层散射
- 超短波超视距绕射
-
随参信道特性
- 衰减随时间变化
- 时延随时间变化
- 多径传播
-
多径效应——多径传播的影响
- 结论
- 多径传播使信号产生瑞利型衰落
- 多径传播引起频率弥散
- 信道对信号不同的频率成分,将有不同的衰减——频率选择性衰落
- 结论
-
减小频率选择性衰落的措施
-
信道相关带宽:
Δ f = 1 / τ m Delta f=1/tau_m Δf=1/τm
定义为相邻传输零点的频率间隔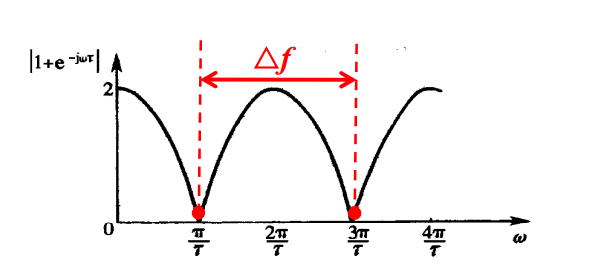
-
应使信号带宽 B s < Δ f B_s<Delta f Bs<Δf,工程经验公式:
B s = ( 1 / 3 ∼ 1 / 5 ) Δ f B_s=(1/3sim1/5)Delta f Bs=(1/3∼1/5)Δf -
数字信号的码元宽度:
T s = ( 3 ∼ 5 ) τ m → R B ↓ T_s=(3sim5)tau_m rightarrow R_Bdownarrow Ts=(3∼5)τm →RB↓
-
-
4.5 信道噪声
- 何谓噪声
- 信道中存在的不需要的电信号
- 它独立于信号始终存在,所有又称加性干扰
- 它使信号失真,发生错码,限制传输速率
- 噪声类型
- 按噪声来源
- 人为噪声
- 自然噪声
- 内部噪声(如热噪声)
- 按噪声性质
- 脉冲噪声
- 窄带/单频噪声
- 起伏噪声(热噪声、散弹噪声和宇宙噪声)
- 按噪声来源
4.6 信道容量
指信道能够无差错传输时的最大平均信息速率
4.6.2 连续信道容量
由香农信息论可证,白噪声背景下的连续信道容量为:
C
=
B
log
2
(
1
+
S
N
)
(
b
/
s
)
—
—
香
农
公
式
C=Blog_2(1+frac{S}{N})(b/s) ——香农公式
C=Blog2(1+NS)(b/s) ——香农公式
等价式:
C
=
B
log
2
(
1
+
S
n
0
B
)
(
b
/
s
)
S
−
信
号
平
均
功
率
(
W
)
;
B
−
带
宽
(
H
z
)
n
0
−
噪
声
单
边
功
率
谱
密
度
;
N
=
n
0
B
−
噪
声
功
率
(
W
)
C=Blog_2(1+frac{S}{n_0B})(b/s)\ S-信号平均功率(W);B-带宽(Hz)\ n_0-噪声单边功率谱密度;N=n_0B-噪声功率(W)
C=Blog2(1+n0BS)(b/s)S−信号平均功率(W);B−带宽(Hz)n0−噪声单边功率谱密度;N=n0B−噪声功率(W)
含义:
当信号和信道噪声的平均功率给定时,在具有一定频带宽度的信道上,理论上单位时间内可能传输的信息量的极限数值
意义:
若 R b ≦ C R_bleqq C Rb≦C ,则总能找到一种信道编码方式,实现无差错传输;若传输速率大于信道容量,则不可能实现无差错传输
结论:
-
信道容量 C 依赖于 B、S 和 n 0 n_0 n0
-
增大 S 可增加 C,若 S → ∞ Srightarrowinfty S→∞,则 C → ∞ Crightarrowinfty C→∞;
-
减小 n 0 n_0 n0 可增加 C,若 n 0 → 0 n_0rightarrow 0 n0→0,则 C → ∞ Crightarrow infty C→∞;
-
增大 B 可增加 C,但不能使 C 无限制增大。
当 B → ∞ Brightarrowinfty B→∞ 时,C 将趋向一个定值:
lim B → ∞ C = lim B → ∞ B log 2 ( 1 + S n 0 B ) ≈ 1.44 S n 0 lim_{Brightarrowinfty}C=lim_{Brightarrowinfty}Blog_2(1+frac{S}{n_0B})approx1.44frac{S}{n_0} B→∞limC=B→∞limBlog2(1+n0BS)≈1.44n0S
应用:
- C 一定时,信道带宽 B、信噪比 S/N、传输时间 t 三者之间可以互相转换
- 增加 B,可以换取 S/N 的降低;反之亦然
- 若 S/N 不变,增加 B,可以换取 t 的减小
最后
以上就是怕孤单花生最近收集整理的关于《通信原理》第4章(信道)学习笔记第 4 章 信道的全部内容,更多相关《通信原理》第4章(信道)学习笔记第内容请搜索靠谱客的其他文章。








发表评论 取消回复