matlab如何绘制传递函数对数幅频特性_开环传递函数是怎样影响系统的？重要参量1/(1+T)与T/(1+T)的释义...

  点击箭头处蓝色字 “iFTrue未来已来”关注我哦~

核心概览

3  重要参量1/(1+T)与T/(1+T)的释义

▼

在上一节中(《反馈对网络传递函数的影响》)，我们可以看到在负反馈系统中，“扰动-输出”闭环传递函数和“给定-输出”闭环传递函数中都包含开环传递函数T(s)这一因子，因而我们可以通过分析开环传递函数T(s)的特性来确定负反馈系统的特性。并且“扰动-输出”闭环传递函数和“给定-输出”闭环传递函数中含有1/(1+T(s))与T(s)/(1+T(s))两个参量，因此我们对这两个参量所代表的意义进行分析。

为了便于说明，我们举一个具体的例子，如图3.1所示的波特图，其对应的开环传递函数为：

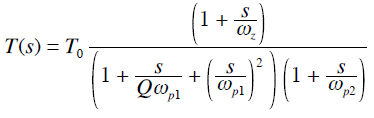
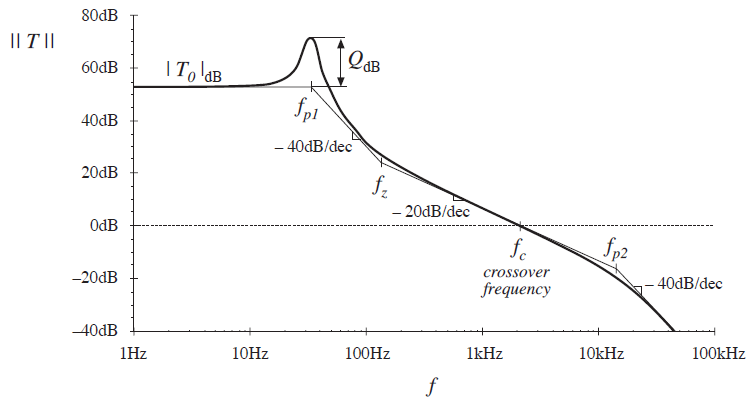
图3.1 开环增益波特图示例

这个例子看起来似乎有点复杂，然而实际开关电源的开环增益往往更为复杂，可能包含4个、5个或更多的极点，但这个例子可以代表我们常见的稳定系统。所以我们可以采用形如图3.1所示的图解法来简化问题。在分析参量|| T/(1+T) ||和|| 1/(1+T) ||的意义之前，首先来看下二者在特定条件下的近似值。

1/(1+T)与T/(1+T)的近似值

当|| T || = 1时，即其对数幅频特性为0dB时，所对应的频率fc称为截止频率，如图3.1所示。由图3.1可知，当频率远远小于截止频率时，即在低频段时，|| T || >> 1，因而1+T ≈ T，则|| T/(1+T) || ≈ 1；当频率远远大于截止频率时，即在高频段时，|| T || << 1，因而1+T ≈ 1，则|| T/(1+T) || ≈ T。

同理，我们可以由图3.1看出，当频率远远小于截止频率时，即在低频段时，|| T || >> 1，则|| 1/(1+T) || ≈ T；当频率远远大于截止频率时，即在高频段时，|| T || << 1，则|| 1/(1+T) || ≈ 1。

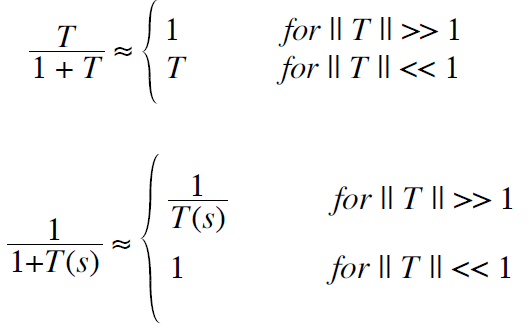
T/(1+T)释义

首先给出结论：参量T/(1+T)对“给定-输出”闭环传递函数有重大影响，其可以反映出低频段时输出电压对给定电压的跟随性。下面进行图形分析。

通过对参量T/(1+T)的近似，我们可以很方便的绘出其所对应的对数幅频特性曲线：当频率较低(f < fc)时，T/(1+T)对数幅频特性近似线接近0dB，当频率较高(f > fc)时，T/(1+T)对数幅频特性近似线跟随T的对数幅频特性近似线，如图3.1所示。 

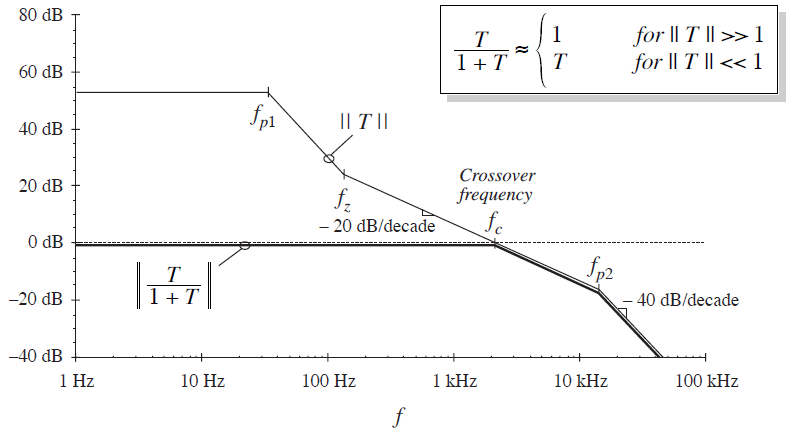
图3.2 || T/(1+T) ||近似线的图形释义

由图3.1可知，当频率远远小于截至频率(低频段)时，开环增益T(s)有较大的幅值。“给定-输出”闭环传递函数可以近似为 

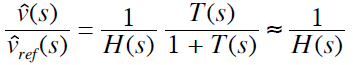
此时，上式表现的是一种期望的系统特性：低频段时，输出电压根据理想增益1/H(s)跟随给定电压。

当频率远远大于截至频率(高频段)时，|| T || < 1，此时T/(1+T) ≈ T，“给定-输出”闭环传递函数为 

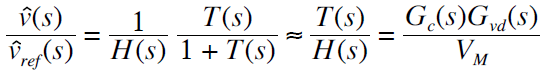
这时的传递函数与“给定-输出”的开环传递函数是一样的，也就是高频段时，相当于移除的反馈环路的作用，反馈环路已经无力抑制干扰，这是由于受到了开环传递函数T带宽的限制，而这是我们不希望得到的特性。

1/(1+T)释义

同样先给出结论：参量1(1+T)对“扰动-输出”闭环传递函数有重大影响，其可以反映出低频段时系统对扰动量(包括线路扰动和负载扰动)的抑制能力。下面进行图形分析。

当频率较低(f < fc)时，|| T || >> 1，1/(1+T) ≈ 1/T，1/(1+T)对数幅频特性近似线接近1/T对数幅频特性近似线(-| T |dB)；当频率较高(f > fc)时，|| T || << 1，1/(1+T) ≈ 1，1/(1+T)对数幅频特性近似线接近0dB。如图3.3所示。

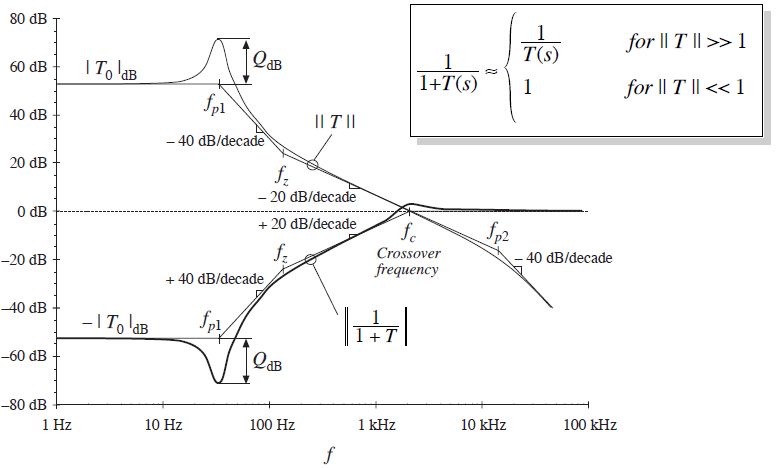
图3.3 || 1/(1+T) ||近似线的图形释义(精确曲线被省略)

当频率远远小于截至频率(低频段)时，开环增益T(s)有较大的幅值。“扰动-输出”传递函数为

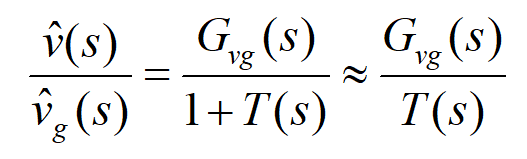
Gvg(s)为原始开环传递函数，可以看出，闭环传递函数的模减小到1/T(s)倍，说明系统对扰动量的抑制了使得扰动量减小到1/T(s)倍。例如，期望扰动传递函数在120Hz的位置减小20倍，则只需要开环传递函数在120Hz的位置对数幅值为(20→26dB)。

对于输出阻抗，存在同样的现象。在频率小于截至频率(低频段)时的闭环输出阻抗为

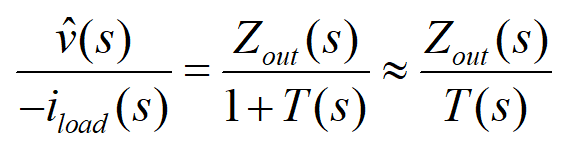
输出阻抗同样减小了1/T(s)倍，因而当负载电流存在变动时，系统对其的抑制使得其反应在输出电压上的值减小到了1/T(s)倍。

当频率大于截至频率(高频段)时，|| T || << 1，1/(1+T) ≈ 1

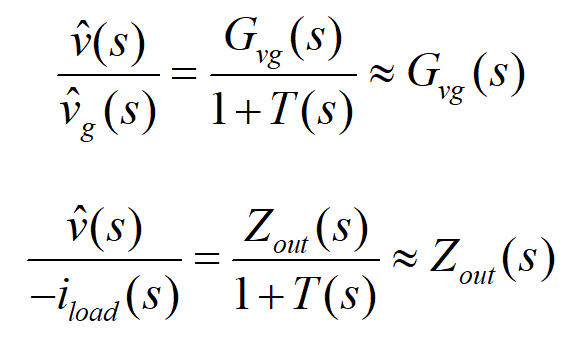
这个结果对于扰动回路和输出阻抗是相同的，可以由上式看出高频段时系统对扰动的抑制仅由开环传递函数决定，表明此时反馈环路将对扰动环节影响甚小，已经无力抑制干扰，这是由于受到了开环传递函数T带宽的限制。因而在设计系统时，开环传递高频段通常要保证能够以-40dB/dec衰减且模足够小。

▼

综上所述，系统开环传递函数在校正时需要保证在低频段有较大的增益，以增强系统输出对给定的跟随性和对扰动的抑制能力；而在高频段时需要保证有迅速衰减且足够小，以增强系统对高频扰动的抑制能力。

欢迎加入交流群，本群供大家进行交流，电力电子、电力传动、DSP控制器、软件算法，只要你有问题都可以在这里交流。

因目前群人数超200人，仅能邀请加入，请添加以下微信，由我拉你入群，注明：加群 + 从事/研究方向，例如：加群 逆变器软件

「 加入交流群 」