方程的根的个数C语言xtu_《自动控制原理》——根轨迹法

根轨迹：闭环系统的特征根随某参数从0到∞变化时的轨迹线。

绘制根轨迹的意义：可以分析系统性能，看出系统的稳准快三项指标随参数的变化会发生什么。

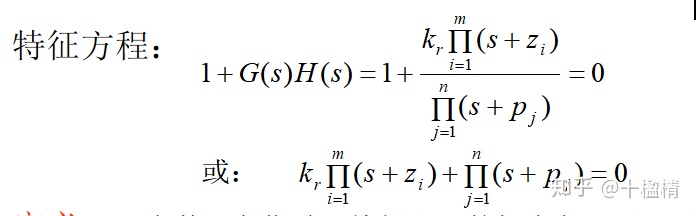
闭环极点：与开环零点、开环极点及 K* 均有关

闭环零点：前向通道零点 + 反馈通道极点

根轨迹的幅值相角条件

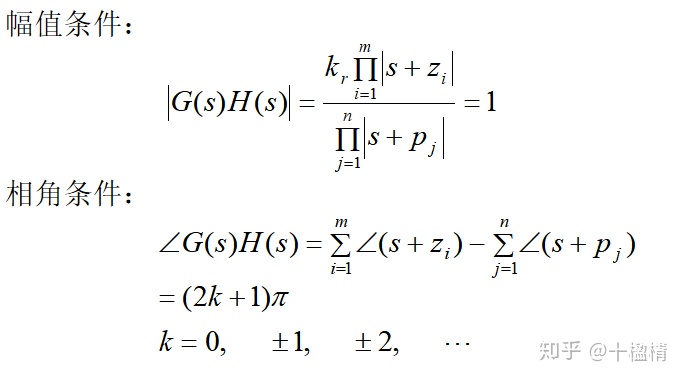
根轨迹的绘制

（一）根轨迹的起点和终点

轨迹起始于开环极点，终止于开环零点；如果开环零点个数少于开环极点个数，则有 n-m 条根轨迹终止于无穷远处。

起点：对应于kr=0

终点：对应于kr→∞

根轨迹起始于开环传递函数的极点，终止于开环传递函数的零点。零点包括m个有限零点和(n-m)个无限零点。

(2) 根轨迹的分支数和对称性

根轨迹的分支数等于开环传递函数的极点数。根轨迹对称于实轴。

(3) 根轨迹在实轴上的分布

从实轴上最右端的开环零、极点算起，奇数开环零、极点到偶数开环零、极点之间的区域必是根轨迹。

两个极点，一个零点时根轨迹的绘制
定理：系统有2个开环极点，1个开环零点，且在复平面存在根轨迹， 则复平面的根轨迹一定是以该零点为圆心的圆弧。

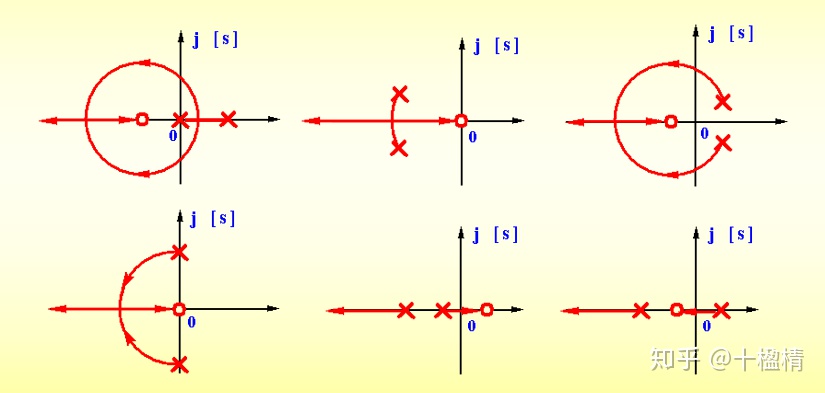
当n-m>2时，闭环极点之和=开环极点之和为一常数

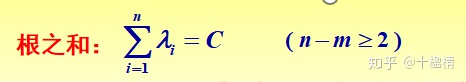
(4) 根轨迹的渐近线

确定了n > m时，n-m条根轨迹分支趋于无穷远处的规律。

(5) 根轨迹的分离点与会合点

试根法，求出近似值

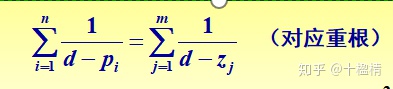
（6） 根轨迹与虚轴的交点

两种求解方法：

用特征方程的实部、虚部方程求解（s=jw）

用劳斯表求解

(7) 根轨迹在开环复极点和复零点的出射角与入射角

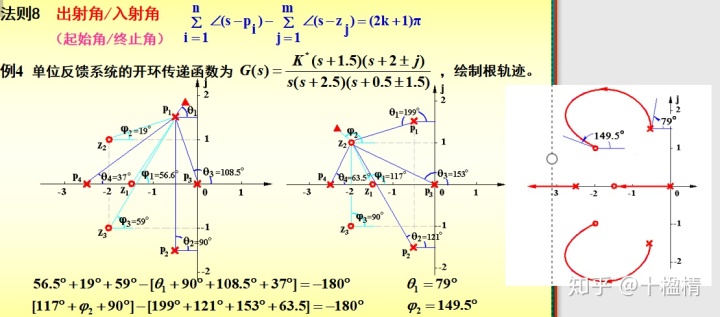
画根轨迹思路：开环传递函数，特征方程，确定n、m，实轴上的轨迹，渐近线，一道题对应的根轨迹不需使用所有的法则，但在特定情况下用什么法则应该清楚。