MATLAB 误差函数erf(x)

误差函数：

1.误差函数定义为：

 　　　　　　　　

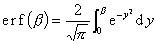
它的性质如下：

　　　　　　　　

　　　　　　　　　

 

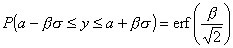
2 互补误差函数定义为：

　　　　　　　　　　

 

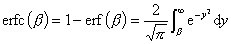
它具有如下性质：

　　　　　　　　　　

　　　　　　　　　　 

　　　　　　　　　　
  

下表给出了误差函数的部分数值：

0.00	0.00000
0.05	0.05637
0.10	0.11246
0.15	0.16800
0.20	0.22270
0.25	0.27633
0.30	0.32863
0.35	0.37938
0.40	0.42839
0.45	0.47548
0.50	0.52050
0.55	0.56332
0.60	0.60386
0.65	0.64203
0.70	0.67780
0.75	0.71116
0.80	0.74210
0.85	0.77067
0.90	0.79691
0.95	0.82089
1.00	0.84270
1.05	0.86244
1.10	0.88021
1.15	0.89612
1.20	0.91031
1.25	0.92290
1.30	0.93401
1.35	0.94376
1.40	0.95229
1.45	0.95970
1.50	0.96611
1.55	0.97162
1.60	0.97635
1.65	0.98038
1.70	0.98379
1.75	0.98667
1.80	0.98909
1.85	0.99111
1.90	0.99279
1.95	0.99418
2.00	0.99532
2.50	0.99959
3.00	0.99998
3.30	0.999998

　　erf 是误差函数，它是高斯概率密度函数的积分。在很多涉及高斯分布的场合，由于理论分析的需要，会涉及到一些关于高斯概率密度函数的积分，这些积分无法求出具体的表达式，可是，这些积分又非常常见，为了表示的需要，后来专门将这类积分定义为erf函数，另外，erfc是互补误差函数，它是在x到无穷上的积分，所以，erfc(x) + erf(x) = 1。