在学习数字信号处理时，有一类很重要的问题是如何判断系统是否为线性时不变（Linear Time Invariant, LTI）系统，由于线性时不变系统具有很多许多的性质，因此判断一个系统是否为LTI系统具有很重要的意义。本文介绍一种使用MATLAB仿真的方法，通过线性性和时不变性两个方面，判断一个系统是否为LTI系统。

问题背景

判断系统是否为线性系统

filter函数介绍

判断系统是否为时不变系统

一、问题背景

已知系统的差分方程如下，判断系统是否为线性时不变系统。

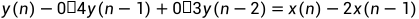
对于此问题，我们分别考虑系统的线性性和时不变性。

二、判断系统是否为线性系统

这里我们考虑使用MATLAB系统中自带的filter函数。

filter函数

1. 求解常系数差分方程

y=filter(b,a,X)
%while b is the factor of y[n], a is the factor of x[n] and X is the input of the system.

线性常系数差分方程形如：

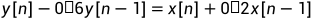
系统的输入为：

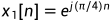
clear all;
close all;
clc;
n=0:100;
x1=exp(1i*(pi/4)*n);
a=[1 0.2];
b=[1 -0.6];
y1=filter(a,b,x1);
stem(n,real(y1));
hold;
stem(n,imag(y1));
xlabel('n');
ylabel('y1');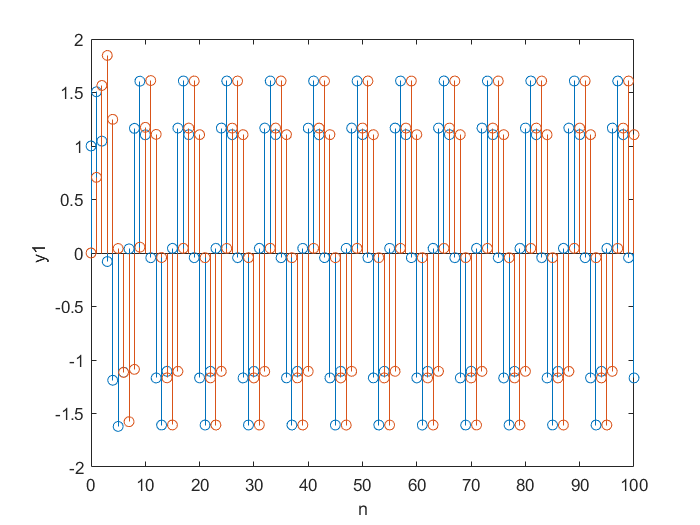

2. 计算卷积

同conv函数一样，filter函数也可计算两个序列的卷积，用它们可以实现相同的运算结果。

h = [3 2 1 2 0 -2 -3 1 0 2];
x = [1,-2 3 -4 1 3 -2];
y = conv(h,x);
n = 0:15;
subplot(2,1,1);
stem(n,y);
xlabel('Time index n');
ylabel('Amplitude');
title('Output Obtained by Convolution');
grid;
n1 = 0:14;
x1 = [x zeros(1,8)];
y1 = filter(h,1,x1);
subplot(2,1,2);
stem(n1,y1);
xlabel('Time index n');
ylabel('Amplitude');
title('Output Generated by Filtering');
grid;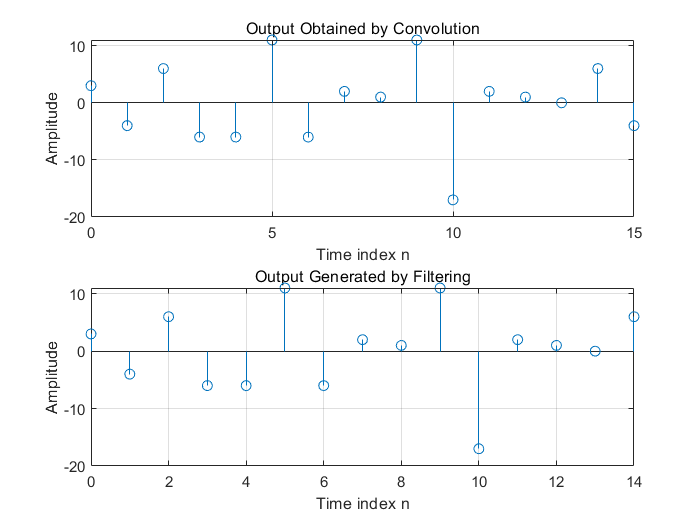

3. 计算冲激响应和阶跃响应

这里我们以单位冲激响应为例。比较filter函数和conv函数对输入冲激序列的输出的异同。

a1 = [1 0.75 0.125];
b1= [1,-1];
n = 0:20;
x1 = [1 zeros(1,20)];
ylfilter = filter(b1,a1,x1);
subplot(1,2,1);
stem(n, ylfilter);
title('ylfilter');
xlabel('x');
ylabel('y');
grid;
x2 = [1 zeros(1,10)];
[h] = impz(b1,a1,10);
ylconv =conv(h,x2);
n = 0:19;
subplot(1,2,2);
stem(n,ylconv,'filled');
titel('ylconv');
xlabel('x');
ylabel('y');
grid;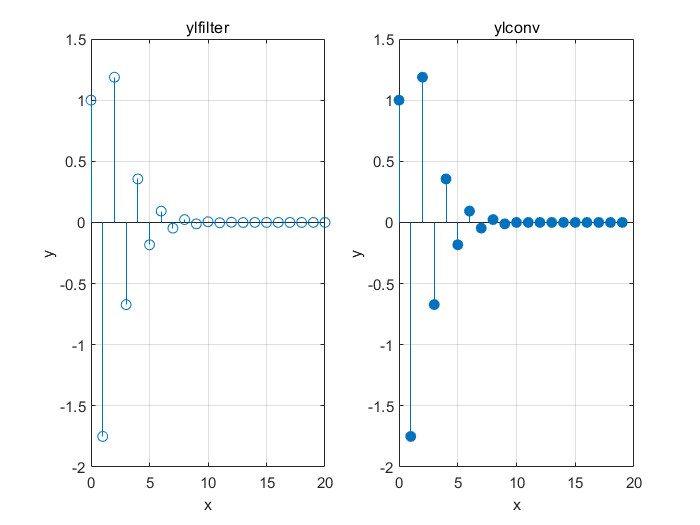

判定系统是否为线性系统

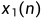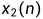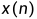设3个不同的输入序列、和，且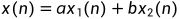，对应的系统输出序列为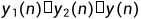.若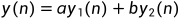，则系统为线性系统。

% judge a system whether has the linear 
n=1:40;
a=2;
b=3;
x1=cos(2*pi*0.1*n);
x2=cos(2*pi*0.4*n);
x=a*x1+b*x2;
num=[1,-2];
den=[1,-0.4,0.3];
y1=filter(num,den,x1);
y2=filter(num,den,x2); %use filter function to solve the system's reaction
y=filter(num,den,x);
yt=a*y1+b*y2;
subplot(2,1,1);
stem(n,y);
title('输出y的振幅');
subplot(2,1,2);
stem(n,yt);
title('输出a*y1+b*y2的振幅');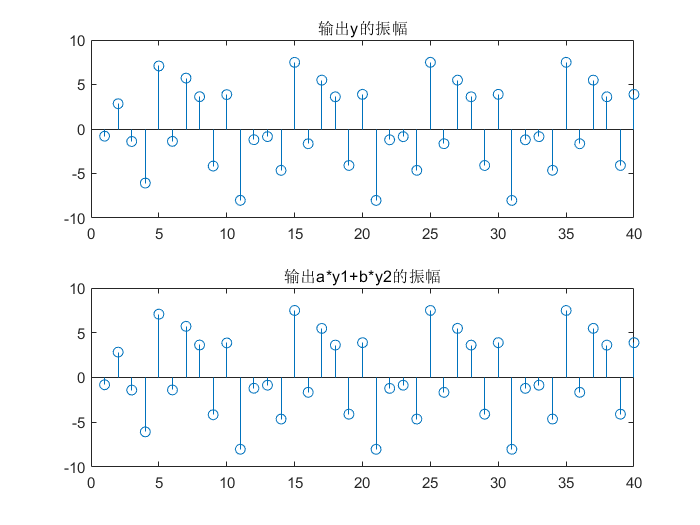

系统线性叠加后输出和两个输入经过系统输出后叠加对比图

通过上图可知，通过系统的输出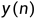满足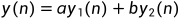，故系统为线性系统。

三、判断系统是否为时不变系统

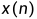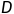通过将输入延迟个单位得到输入为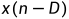，比较系统对于两个输入是否得到两个相同的输出序列（仅时延不同），若是则系统具有时不变性；反之，系统是时变的。

% judge a system whether has time invariant
n=1:40;
D=9;
a=3;
b=5;
x=a*cos(2*pi*0.1*n)+b*cos(2*pi*0.4*n);
xd=[zeros(1,D),x];
num=[1,-2];
den=[1,-0.4,0.3];
y=filter(num,den,x);
yd=filter(num,den,xd);
subplot(2,1,1);
stem(y);
title('输出为x(n)时的输出');
subplot(2,1,2);
stem(yd);
title('输出为x(n-D)时的输出');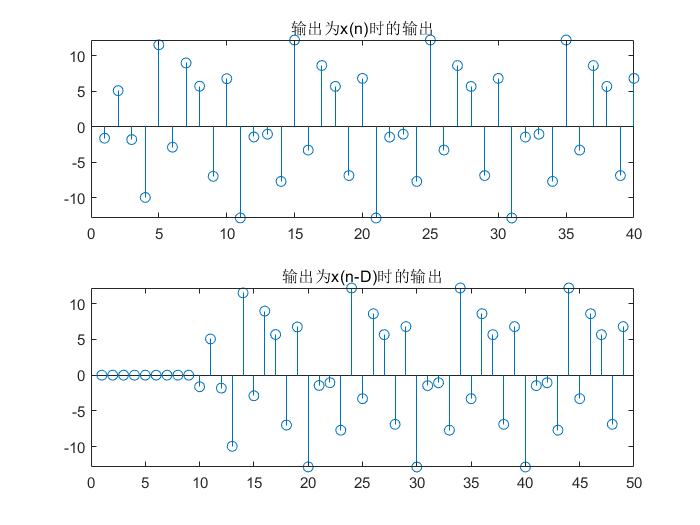

系统针对一个序列和其延时序列的输出示意图

通过对比系统对输入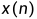和其延迟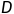个单位得到输入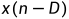的输出，二者仅差一个时延D,故系统是时不变的。

综上，系统满足线性性和时不变性，因此系统是线性时不变系统。