实验（2）信号与系统的时域分析

109 阅读 0 评论 72 点赞

我是靠谱客的博主欢呼手套，这篇文章主要介绍实验（2）信号与系统的时域分析，现在分享给大家，希望可以做个参考。

本文的pdf文件：link

一、实验目的

建立线性时不变离散系统的差分方程和系统输入序列的数学模型，产生输入序列；利用matlab信号处理工具箱的差分方程求解库函数设计程序，求解系统的单位脉冲响应，给定输入序列和系统初始状态的系统响应；利用卷积计算库函数设计程序，计算给定输入序列的系统零状态响应。通过实验深刻理解离散信号与系统的时域性质和分析方法，熟练掌握利用matlab工具时域分析离散信号和系统的方法。

二、实验原理

离散时间系统在数学上定义为将输入序列x(n)映射成输出序列y(n)的唯一性变换或运算，亦即将一个序列变换成另一个序列的系统。设变换或运算关系用T[﹒]表示，则系统输出序列y(n)与输入序列x(n)之间的关系可表示为
$y (n) = T [x (n)]$
离散时间系统分为线性时不变系统、线性时变系统、非线性时不变系统和非线性时变系统。其中最重要的是线性时不变系统。

2.1 线性系统

满足线性叠加原理的系统称为线性系统。设x1(n)和x2(n)分别为系统的输入序列，其输出序列分别用y1(n),y2(n)表示，即
$y_1 (n) = T[x_1 (n)]$
$y_2 (n) = T[x_2 (n)]$
那么线性系统一定满足下面两个公式：

$T[x_1 (n)+x_2 (n)]= T[x_1 (n)]+T[x_2 (n)]$
$T[a*x_1 (n)]= a*T[x_1 (n)]$

满足上两式表示分别表示线性系统的可加性和齐次性。

2.2 时不变系统

如果系统对输入序列的运算关系在整个过程中不随时间变化，则这种系统称为时不变系统。用公式表示如下：
$y (n) = T [x (n)]$
$y(n-n_0 ) = T[x(n-n_0 )]$

2.3 线性时不变系统的差分方程表示

描述一个系统，可以不考虑系统的内部结构，而只研究系统输出信号与输入信号及系统参数之间的关系。
一个N阶线性常系数差分方程表示为

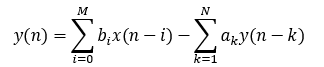
在这里插入图片描述
式中，x(n)和y(n)分别是系统的输入序列和输出序列。

三、输入序列

3.1 方波

Matlab中的square函数，Square（T）函数产生一个2*pi为周期的方波，范围在-1~1之间，占空比为50%，square(T, duty), duty是一个百分数,duty = 75(75%的占空比）。
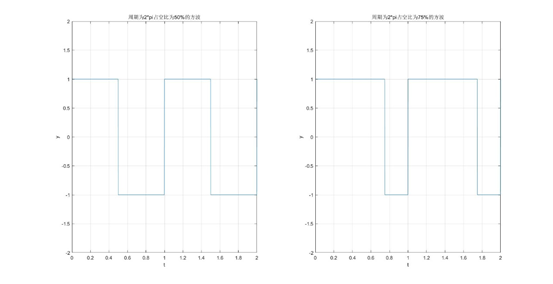
在这里插入图片描述

3.2 连续或者离散的脉冲串

Pulstran(t,d,’func’)，其中t为时间轴，一般是一个一维数组，d为采样间隔，可以是两列，第一列对应偏移量，第二列对应增益量。连续函数func指定了脉冲串的形状，包括：
高斯调制正弦信号：gauspuls；非周期的矩形信号：rectpuls；非周期的三角信号：tripuls
产生一串高斯脉冲。

复制代码

1
2
3
4
5
6
t=0:0.001:8;
d=[0:1:8;0.8,0.8,0.8,0.8,0.8,0.8,0.8,0.8,0.8]';
y=pulstran(t-0.25,d,'gauspuls',10,0.5);
plot(t,y); 
grid；

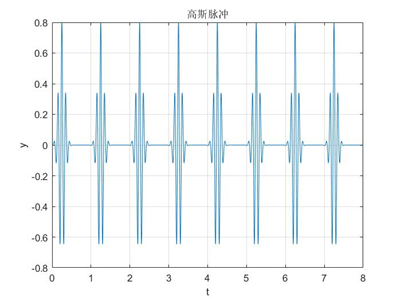
在这里插入图片描述

四、单位脉冲响应

设置系统的差分方程如下：

$y (n) - y (n - 1) + 0.9 y (n - 2) = x (n)$

       设定其y(1)=0,y(2)=1,x(n)为恒为1的序列。
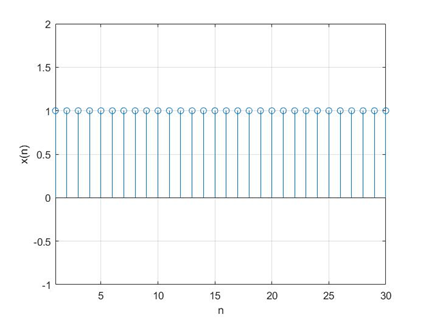
在这里插入图片描述
       根据其初始状态可以求解得到其输出序列y(n):

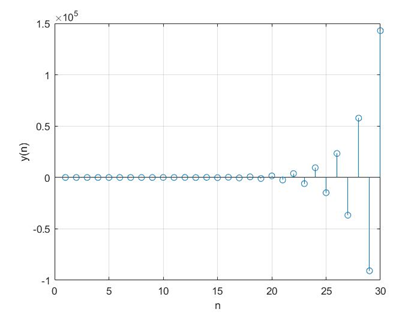
       该系统的单位脉冲响应如下：

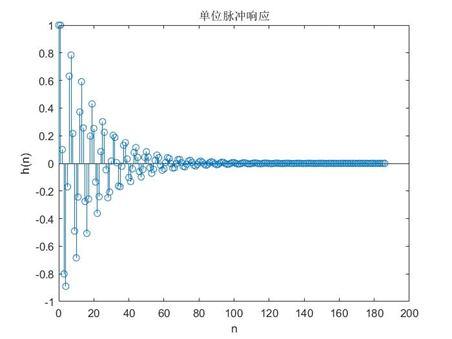
五任意输入序列响应

       设系统的输入序列为x(n)，将他表示成单位脉冲序列的移位加权和，即
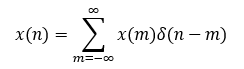
在这里插入图片描述
       那么系统的输出序列为

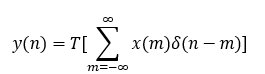
       根据线性系统的叠加原理，上式可表示为

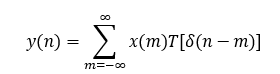
       又根据时不变系统的时不变性质，最终表示为

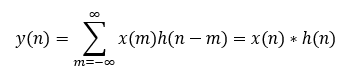
       上式“*”代表线性卷积运算。上式表明，离散时间系统的输出序列等于输入序列与该系统的单位脉冲响应的线性卷积。

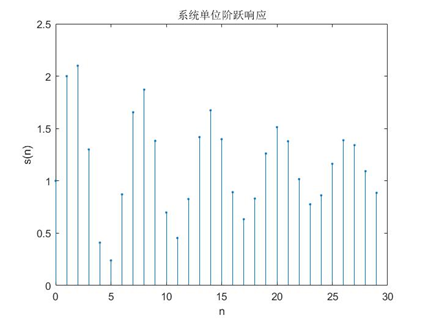
六系统的单位阶跃响应

设置系统的差分方程如下：
$y (n) - y (n - 1) + 0.9 y (n - 2) = x (n)$
设定其y(1)=0,y(2)=1,x(n)为恒为1的序列。
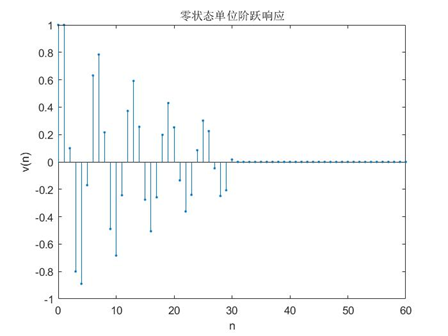
在这里插入图片描述

七、matlab代码

复制代码

% 建立线性时不变离散系统的差分方程和系统输入序列的数学模型，产生输入序列；
% 利用matlab信号处理工具箱的差分方程求解库函数设计程序，求解系统的单位脉冲响应，
% 给定输入序列和系统初始状态的系统响应；
% 利用卷积计算库函数设计程序，计算给定输入序列的系统零状态响应。
% 通过实验深刻理解离散信号与系统的时域性质和分析方法，熟练掌握利用matlab工具时域分析离散信号和系统的方法。
 
% 产生输入序列，根据函数来确定输入序列
% 产生方波
t = 0:0.001:2;
figure(1)
subplot(1,2,1)
y1 = square(2.*pi.*t); 
plot(t,y1);
xlabel('t');
ylabel('y');
title('周期为2*pi占空比为50%的方波');
ylim([-2,2]);
grid on;
figure(1)
subplot(1,2,2)
y2 = square(2.*pi.*t,75); 
plot(t,y2);
xlabel('t');
ylabel('y');
title('周期为2*pi占空比为75%的方波');
ylim([-2,2]);
grid on;
% 产生脉冲串
t=0:0.001:8;
d=[0:1:8;0.8,0.8,0.8,0.8,0.8,0.8,0.8,0.8,0.8]';
figure(2);
y1=pulstran(t-0.25,d,'gauspuls',10,0.5);
plot(t,y1);
xlabel('t');
ylabel('y');
title('高斯脉冲');
grid on;
% 建立线性时不变离散系统，该系统用离散方程表示
y(1)=0;
y(2)=1;
x=ones(1,30);
for n=3:30
    y(n)=x(n)-y(n-1)+0.9*y(n-2);
end
figure(3)
stem(1:30,y);
xlabel('n');
ylabel('y(n)');
grid on;
figure(4)
stem(1:30,x);
xlabel('n');
ylabel('x(n)');
xlim([1,30]);
ylim([-1,2]);
grid on;
b = [1];
a = [1,-1,0.9];
n=[1:20]';
[h,t] = impz(b,a,n);
figure(5)
stem(t,h);
title('单位脉冲响应');
xlabel('n');
ylabel('h(n)');
 
% 假设系统仍为上述所求解的差分方程
% 随意设定输入序列
x=[1,2,3,4,5,6,7,8,9,10,1,2,3,4,5,6,7,8,9,10];
%1,直接带入差分方程求解系统输出
y(1)=0;
y(2)=1;
for n=3:20
    y(n)=x(n)-y(n-1)+0.9*y(n-2);
end
figure(6)
stem(1:20,x);
xlabel('n');
ylabel('x(n)');
xlim([1,20]);
ylim([0,11]);
grid on;
figure(7)
stem(1:20,y);
xlabel('n');
ylabel('y(n)');
grid on;
out=conv(x,h);
figure(8)
stem(1:20,out(1:20));
ys=0;
xn=[1,zeros(1,30)];
B=1;
A=[1,-1,0.9];
xi=filtic(B,A,ys);
hn=filter(B,A,xn,xi);
n=0:length(hn)-1;
figure(1)
stem(n,hn,'.');
title('系统单位脉冲响应');
xlabel('n');
ylabel('h(n)');
xn=ones(1,30);%单位阶跃序列
sn=filter(B,A,xn,xi);
figure(2)
n=0:length(sn)-1;
stem(n,sn,'.');
title('系统单位阶跃响应');
xlabel('n');
ylabel('s(n)');
x=[1,zeros(1,30)];
vn=conv(x,hn);
n=0:length(vn)-1;
figure(3)
stem(n,vn,'.');
title('零状态单位阶跃响应');
xlabel('n');
ylabel('v(n)');

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
% 建立线性时不变离散系统的差分方程和系统输入序列的数学模型，产生输入序列；
% 利用matlab信号处理工具箱的差分方程求解库函数设计程序，求解系统的单位脉冲响应，
% 给定输入序列和系统初始状态的系统响应；
% 利用卷积计算库函数设计程序，计算给定输入序列的系统零状态响应。
% 通过实验深刻理解离散信号与系统的时域性质和分析方法，熟练掌握利用matlab工具时域分析离散信号和系统的方法。
 
% 产生输入序列，根据函数来确定输入序列
% 产生方波
t = 0:0.001:2;
figure(1)
subplot(1,2,1)
y1 = square(2.*pi.*t); 
plot(t,y1);
xlabel('t');
ylabel('y');
title('周期为2*pi占空比为50%的方波');
ylim([-2,2]);
grid on;
figure(1)
subplot(1,2,2)
y2 = square(2.*pi.*t,75); 
plot(t,y2);
xlabel('t');
ylabel('y');
title('周期为2*pi占空比为75%的方波');
ylim([-2,2]);
grid on;
% 产生脉冲串
t=0:0.001:8;
d=[0:1:8;0.8,0.8,0.8,0.8,0.8,0.8,0.8,0.8,0.8]';
figure(2);
y1=pulstran(t-0.25,d,'gauspuls',10,0.5);
plot(t,y1);
xlabel('t');
ylabel('y');
title('高斯脉冲');
grid on;
% 建立线性时不变离散系统，该系统用离散方程表示
y(1)=0;
y(2)=1;
x=ones(1,30);
for n=3:30
    y(n)=x(n)-y(n-1)+0.9*y(n-2);
end
figure(3)
stem(1:30,y);
xlabel('n');
ylabel('y(n)');
grid on;
figure(4)
stem(1:30,x);
xlabel('n');
ylabel('x(n)');
xlim([1,30]);
ylim([-1,2]);
grid on;
b = [1];
a = [1,-1,0.9];
n=[1:20]';
[h,t] = impz(b,a,n);
figure(5)
stem(t,h);
title('单位脉冲响应');
xlabel('n');
ylabel('h(n)');
 
% 假设系统仍为上述所求解的差分方程
% 随意设定输入序列
x=[1,2,3,4,5,6,7,8,9,10,1,2,3,4,5,6,7,8,9,10];
%1,直接带入差分方程求解系统输出
y(1)=0;
y(2)=1;
for n=3:20
    y(n)=x(n)-y(n-1)+0.9*y(n-2);
end
figure(6)
stem(1:20,x);
xlabel('n');
ylabel('x(n)');
xlim([1,20]);
ylim([0,11]);
grid on;
figure(7)
stem(1:20,y);
xlabel('n');
ylabel('y(n)');
grid on;
out=conv(x,h);
figure(8)
stem(1:20,out(1:20));
ys=0;
xn=[1,zeros(1,30)];
B=1;
A=[1,-1,0.9];
xi=filtic(B,A,ys);
hn=filter(B,A,xn,xi);
n=0:length(hn)-1;
figure(1)
stem(n,hn,'.');
title('系统单位脉冲响应');
xlabel('n');
ylabel('h(n)');
xn=ones(1,30);%单位阶跃序列
sn=filter(B,A,xn,xi);
figure(2)
n=0:length(sn)-1;
stem(n,sn,'.');
title('系统单位阶跃响应');
xlabel('n');
ylabel('s(n)');
x=[1,zeros(1,30)];
vn=conv(x,hn);
n=0:length(vn)-1;
figure(3)
stem(n,vn,'.');
title('零状态单位阶跃响应');
xlabel('n');
ylabel('v(n)');

最后

以上就是欢呼手套最近收集整理的关于实验（2）信号与系统的时域分析的全部内容，更多相关实验（2）信号与系统内容请搜索靠谱客的其他文章。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。

本文分类：数字信号处理
浏览次数：109 次浏览
发布日期：2023-05-22 07:48:01
本文链接：https://www.kaopuke.com/article/k-p-k_14_ujocfz_13__23__14_2.html

实验（2）信号与系统的时域分析

一、实验目的

二、实验原理

2.1 线性系统

2.2 时不变系统

2.3 线性时不变系统的差分方程表示

三、输入序列

3.1 方波

3.2 连续或者离散的脉冲串

四、单位脉冲响应

五任意输入序列响应

六系统的单位阶跃响应

七、matlab代码

最后

评论列表共有 0 条评论

发表评论取消回复

实验（2）信号与系统的时域分析

一、实验目的

二、实验原理

2.1 线性系统

2.2 时不变系统

2.3 线性时不变系统的差分方程表示

三、输入序列

3.1 方波

3.2 连续或者离散的脉冲串

四、单位脉冲响应

五 任意输入序列响应

六 系统的单位阶跃响应

七、matlab代码

最后

相关文章

评论列表共有 0 条评论

发表评论 取消回复

微信扫一扫：分享

五任意输入序列响应

六系统的单位阶跃响应

发表评论取消回复