Matlab 构建系统 绘制零极点

>> num0 = 5*[1 5 6]; den0 = [1 6 10 8]; % 描述闭环传递函数的分子、分母多项式
>> sys0 = tf(num0, den0) % 高阶系统建模

sys0 =
 
    5 s^2 + 25 s + 30
  ----------------------
  s^3 + 6 s^2 + 10 s + 8
 
Continuous-time transfer function.

>> den0 = [1 6 10 8]; % 描述C(s)的分母多项式
>> [z,p,k] = tf2zp(num0, den0) % 对传递函数进行因式分解

z =

   -3.0000
   -2.0000


p =

  -4.0000 + 0.0000i
  -1.0000 + 1.0000i
  -1.0000 - 1.0000i


k =

     5

>> sys = zpk(z, p, k) % 给出闭环传递函数的零极点形式

sys =
 
     5 (s+3) (s+2)
  --------------------
  (s+4) (s^2 + 2s + 2)
 
Continuous-time zero/pole/gain model.

>> [r, p, k] = residue(num0, den) % 部分分式展开

r =

  -0.2500 + 0.0000i
  -1.7500 - 0.2500i
  -1.7500 + 0.2500i
   3.7500 + 0.0000i


p =

  -4.0000 + 0.0000i
  -1.0000 + 1.0000i
  -1.0000 - 1.0000i
   0.0000 + 0.0000i


k =

     []

>> step(sys0) % 计算高阶系统的单位阶跃响应

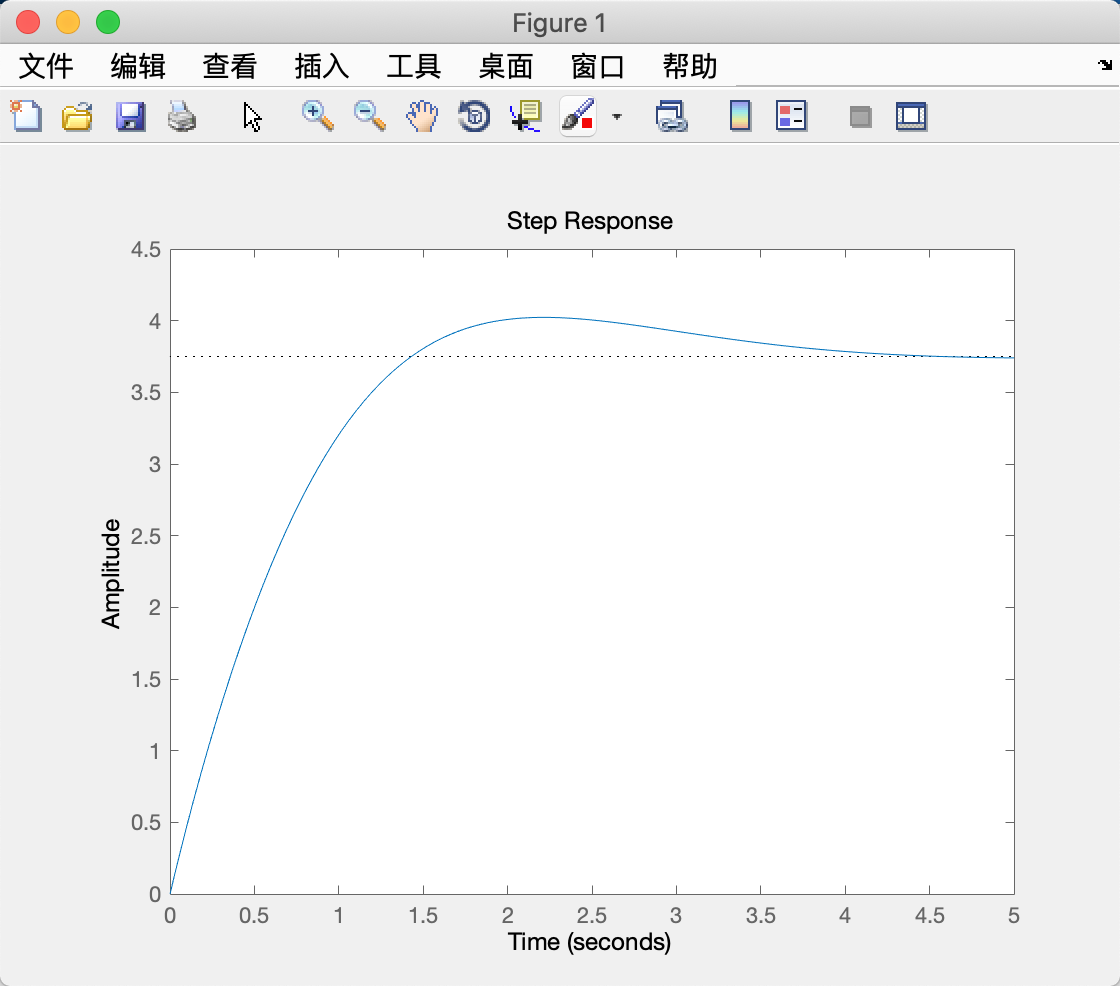
From: 《自动控制原理第六版》胡寿松-P91

>> pzmap(sys0) % 绘制零极点

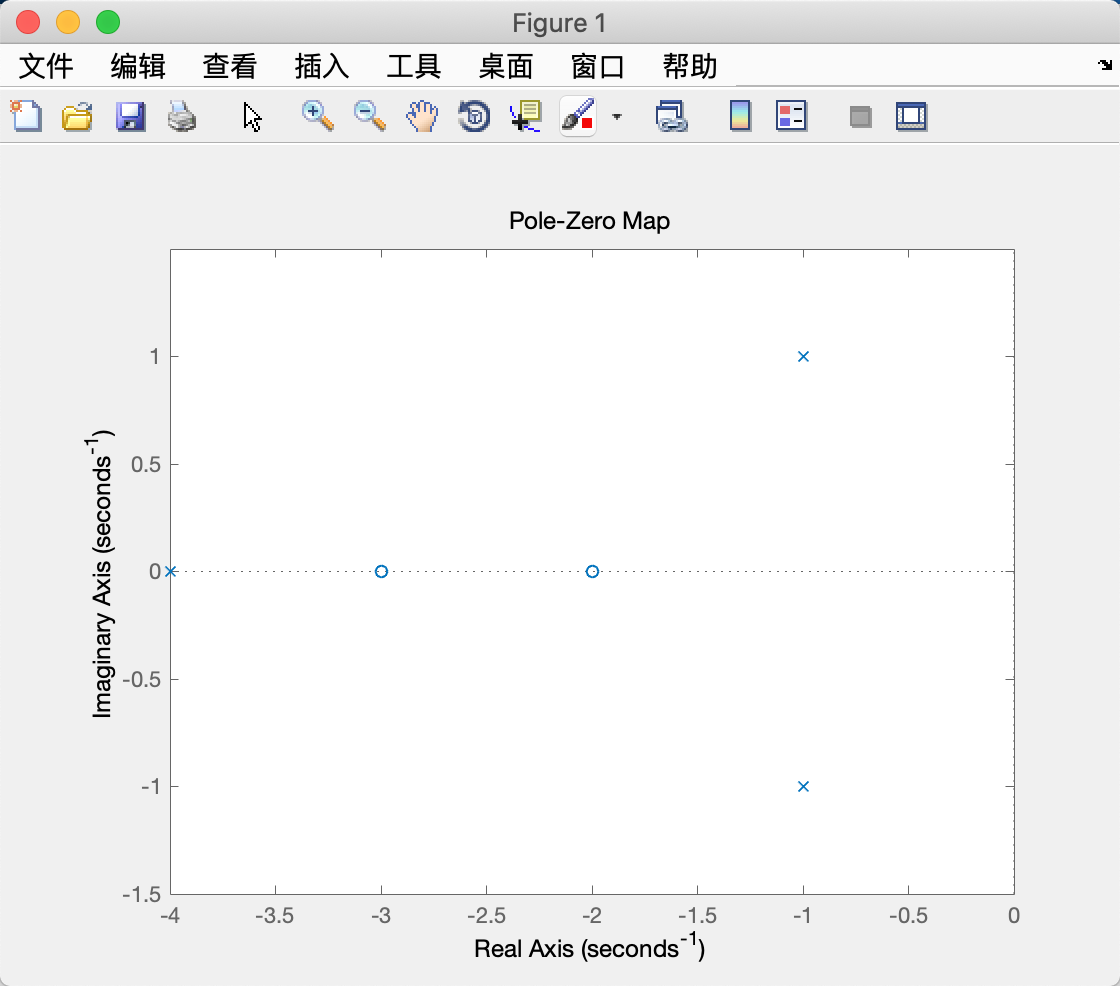
>> sys = zpk([-2.1], [-8 -2 -0.5+0.866*j -0.5-0.866*j], 8) % 原四阶系统建模

sys =
 
          8 (s+2.1)
  -------------------------
  (s+8) (s+2) (s^2 + s + 1)
 
Continuous-time zero/pole/gain model.

>> sysl = tf([1.05], [1 1 1]) % 由原系统近似的二阶系统

sysl =
 
     1.05
  -----------
  s^2 + s + 1
 
Continuous-time transfer function.

>> step(sys, 'b-', sysl, 'r:') % 绘制系统的阶跃响应曲线

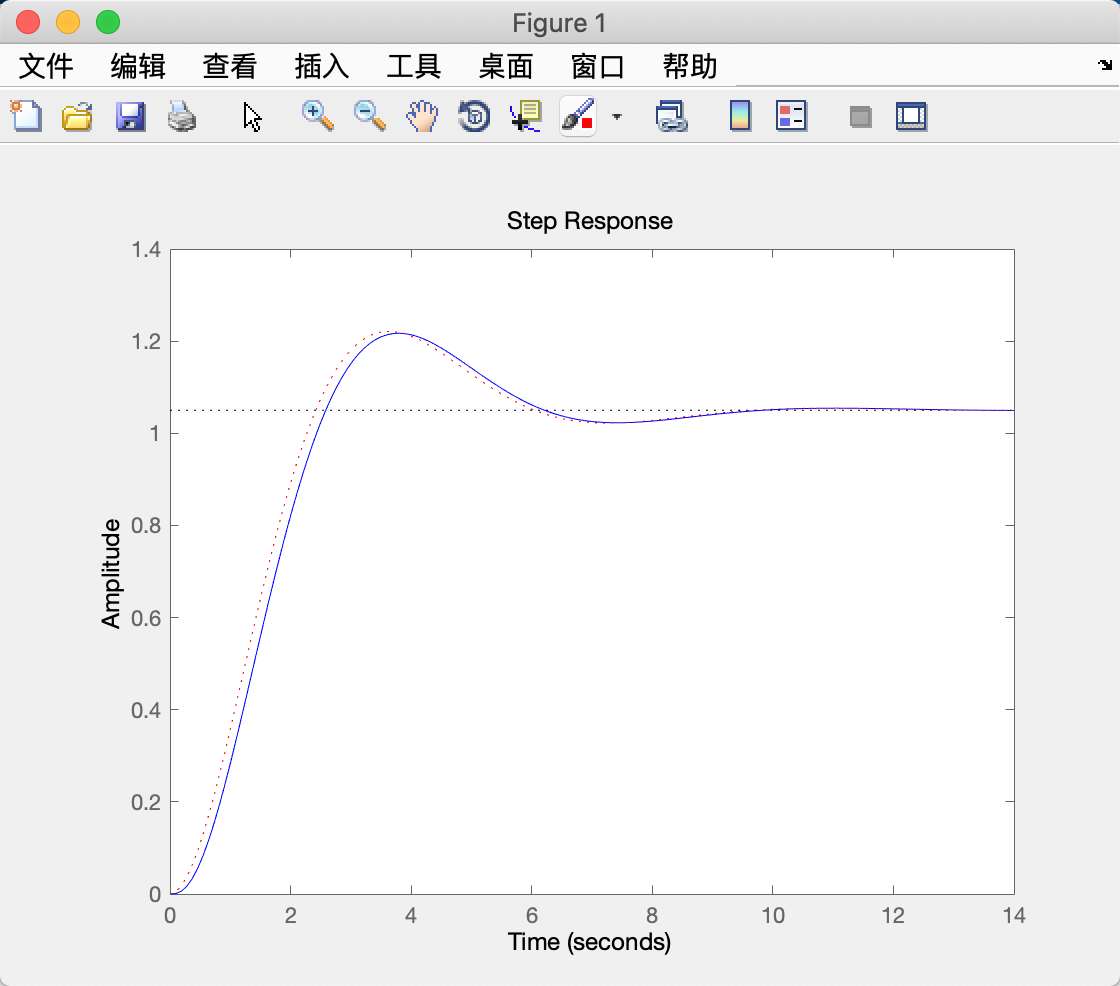
From: 《自动控制原理第六版》胡寿松-P92

最后

以上就是粗犷音响为你收集整理的【Matlab 控制】构建系统，绘制零极点Matlab 构建系统 绘制零极点的全部内容，希望文章能够帮你解决【Matlab 控制】构建系统，绘制零极点Matlab 构建系统 绘制零极点所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。