qpsk相点 matlab,qpsk调制解调matlab仿真程序详解

qpsk调制解调matlab仿真程序详解

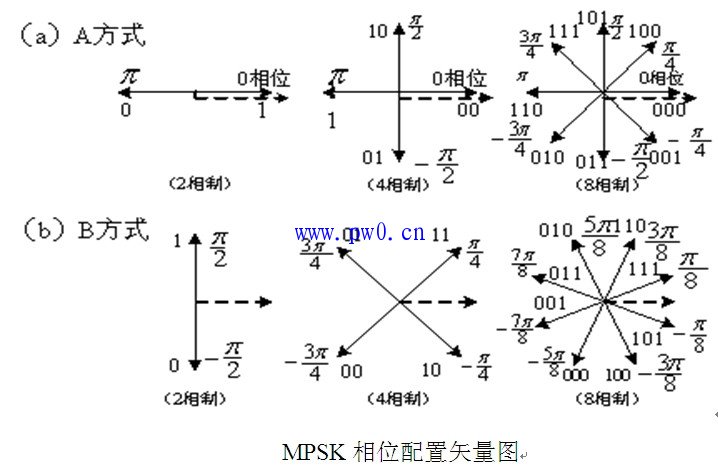
注意B方式的4PSK用的比较多。I 路信号是用余弦载波，由2进制数据流的奇数序列组成；Q路信号用正弦载波，由2进制数据流的偶数序列组成。下面的a是Idata，b就是Qdata，它们分布与各自的载波相乘分别输出 I 路信号和 Q 路信号。I 路信号加上Q路信号就是QPSK输出信号。当 I 路载波信号是0相位时为1，是180°相位时为0；当Q路载波信号是0相位时为1，是180°相位时为0。比如下图的‘11’数据cos(theta) + sin(theta) = sqrt(2)*sin(theta + 45°)是相位超前sin(theta) 45°

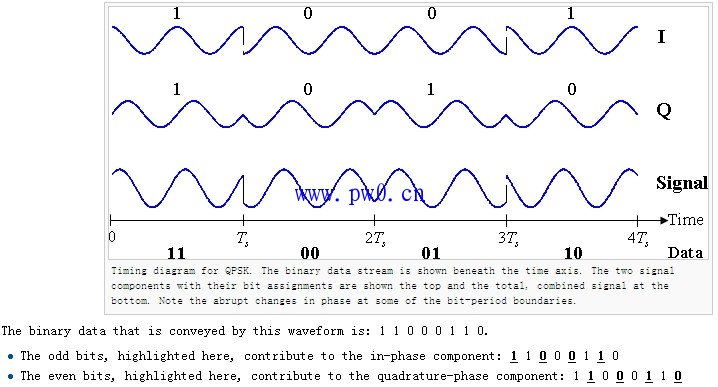
QPSK即四进制移向键控(Quaternary Phase Shift Keying)，它利用载波的四种不同相位来表示数字信息，由于每一种载波相位代表两个比特信息，因此每个四进制码元可以用两个二进制码元的组合来表示。两个二进制码元中的前一个码元用a表示，后一个码元用b表示。

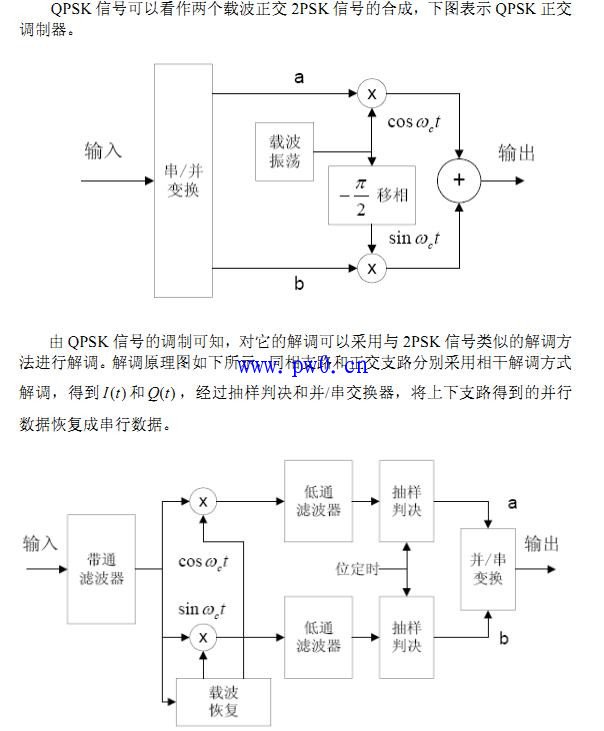
% QPSK调相法基本原理解释

clear all

close all

% x1是类似[1 1 -1 -1 -1 -1 1 1]的分布,作用是控制相位的180°反转。

%由于仿真中载波的频率是f=1Hz，所以1s的间隔内有一个完整周期的正弦波

t=[-1:0.01:7-0.01]; % t共800个数据，-1~7s

t1 = [0:0.01:8-0.01]; %t1也是800个数据点 ，0 ~8s

tt=length(t); % tt=800

x1=ones(1,800);

for i=1:tt

if (t(i)>=-1 & t(i)=5& t(i)

x1(i)=1;

else x1(i)=-1;

end

end

t2 = 0:0.01:7-0.01; %t2是700个数据点，是QPSK_rc绘图的下标

t3 = -1:0.01:7.1-0.01; %t3有810个数据点，是i_rc的时间变量

t4 = 0:0.01:8.1-0.01; %t4有810个数据点，是q_rc的时间变量

%x2是类似于[1 1 -1 -1 1 1 1 1]的分布,作用是控制相位的180°反转

tt1=length(t1);

x2=ones(1,800);

for i=1:tt1

if (t1(i)>=0 & t1(i)=4& t1(i)

x2(i)=1;

else x2(i)=-1;

end

end

f=0:0.1:1;

xrc=0.5+0.5*cos(pi*f); %xrc是一个低通特性的传输函数

y1=conv(x1,xrc)/5.5; %y1和x1 实际上没什么区别，仅仅是上升沿、下降沿有点过渡带

y2=conv(x2,xrc)/5.5; % y2和x2 实际上没什么区别，仅仅是上升沿、下降沿有点过渡带

n0=randn(size(t2));

f1=1;

i=x1.*cos(2*pi*f1*t); % x1就是I data

q=x2.*sin(2*pi*f1*t1); %x2就是Q data

I=i(101:800);

Q=q(1:700);

QPSK=sqrt(1/2).*I+sqrt(1/2).*Q;

QPSK_n=(sqrt(1/2).*I+sqrt(1/2).*Q)+n0;

n1=randn(size(t2));

i_rc=y1.*cos(2*pi*f1*t3); % y1就是I data，i_rc可能是贴近实际的波形,i则是理想波形

q_rc=y2.*sin(2*pi*f1*t4); %y2就是Q data，q_rc可能是贴近实际的波形,q则是理想波形

I_rc=i_rc(101:800);

Q_rc=q_rc(1:700);

QPSK_rc=(sqrt(1/2).*I_rc+sqrt(1/2).*Q_rc);

QPSK_rc_n1=QPSK_rc+n1;

figure(1)

subplot(4,1,1);plot(t3,i_rc);axis([-1 8 -1 1]);ylabel('a序列');

subplot(4,1,2);plot(t4,q_rc);axis([-1 8 -1 1]);ylabel('b序列');

subplot(4,1,3);plot(t2,QPSK_rc);axis([-1 8 -1 1]);ylabel('合成序列');

subplot(4,1,4);plot(t2,QPSK_rc_n1);axis([-1 8 -1 1]);ylabel('加入噪声');

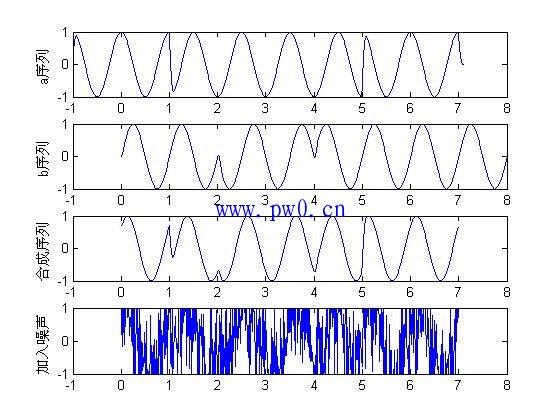
上图解释： 合成序列表示的数据：11 01 00 00 01 11 11

相对于sin(theta)合成序列相位: Pi/4, 3/4Pi[即sin(theta-45)=sin(theta-45+180)],

-3/4Pi[即-sin(theta+45)], -3/4Pi[即-sin(theta+45)] , 3/4Pi, Pi/4, Pi/4。

例1

% 设定 T=1,加入均匀分布噪声

clear all

close all

% 调制

bit_in = randint(1e3, 1, [0 1]);

bit_I = bit_in(1:2:1e3); %bit_I为”奇数序列”，奇数序列是同相分量，以cos为载波

bit_Q = bit_in(2:2:1e3); %bit_Q是bit_in的所有偶数下标组成的”偶数序列”，以sin为载波

data_I = -2*bit_I+1; % 将bit_I中的1变成-1，0变成1; 注意data_I是500点

data_Q = -2*bit_Q+1; %将bit_Q中的1变成-1，0变成1

data_I1=repmat(data_I',20,1); %将500行的列向量data_I的共轭转置data_I’复制为20*500的矩阵，20行数据是相同的。

data_Q1=repmat(data_Q',20,1);

for i=1:1e4 %data_I2是将data_I1这个20*500的矩阵拉长为1*10000的行向量

data_I2(i)=data_I1(i); %注意索引方式是按列计数20个数恰好是同一个数，这是后面20个数加起来判决的依据

data_Q2(i)=data_Q1(i);

end;

f=0:0.1:1;

xrc=0.5+0.5*cos(pi*f); %xrc是一个长度为11的低通特性传输函数,L=11

data_I2_rc=conv(data_I2,xrc)/5.5; % data_I2_rc就是Idata

data_Q2_rc=conv(data_Q2,xrc)/5.5; % data_Q2_rc就是Qdata

f1=1;

t1=0:0.1:1e3+0.9; % 10010个数据，长度和data_I2_rc以及data_Q2_rc相同

n0=rand(size(t1)); %n0是1*10010的均匀分布的噪声

I_rc=data_I2_rc.*cos(2*pi*f1*t1);

Q_rc=data_Q2_rc.*sin(2*pi*f1*t1);

QPSK_rc=(sqrt(1/2).*I_rc+sqrt(1/2).*Q_rc);

QPSK_rc_n0=QPSK_rc+n0;

% 解调(相干解调，与载波相乘)

I_demo=QPSK_rc_n0.*cos(2*pi*f1*t1); % I_demo和QPSK_rc_n0长度相等均为10010

Q_demo=QPSK_rc_n0.*sin(2*pi*f1*t1);

% 低通滤波

I_recover=conv(I_demo,xrc);

Q_recover=conv(Q_demo,xrc);

I=I_recover(11:10010); %去掉两头10个数据，由于单次FIR群延时造成的(L-1)/2=5，两次滤波恰好是10个点。

Q=Q_recover(11:10010);

t2=0:0.05:1e3-0.05; %t2有20000个点

t3=0:0.1:1e3-0.1; %t3有10000个点

% 抽样判决

data_recover=[];

for i=1:20:10000 %data_recover是待判决的20000点

data_recover=[data_recover I(i:1:i+19) Q(i:1:i+19)];

end;

bit_recover=[];

for i=1:20:20000

if sum(data_recover(i:i+19))>0 %20点为同一个值，20点数据叠加后与阈值0比较

data_recover_a(i:i+19)=1; %data_recover_a是并/串转换后的20000点

bit_recover=[bit_recover 1]; %bit_recover是1000点数据

else

data_recover_a(i:i+19)=-1;

bit_recover=[bit_recover -1];

end

end

error=0;

dd = -2*bit_in+1; % 将bit_in中的1变成-1，0变成1

ddd=[dd']; %ddd是1表示0，-1表示1的原始序列，1000个点

ddd1=repmat(ddd,20,1); %ddd1是20*1000的矩阵

for i=1:2e4

ddd2(i)=ddd1(i); %将ddd1拉直为1*20000的行向量ddd2

end

for i=1:1e3

if bit_recover(i)~=ddd(i)

error=error+1;

end

end

p=error/1000;

figure(1)

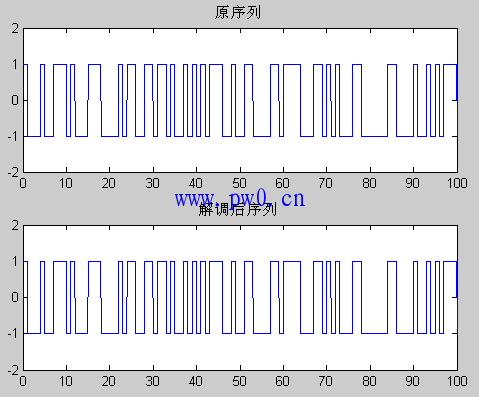
subplot(2,1,1);plot(t2,ddd2);axis([0 100 -2 2]);title('原序列');

subplot(2,1,2);plot(t2,data_recover_a);axis([0 100 -2 2]);title('解调后序列');

例2

clear all

close all

% 调制

bit_in = randint(1e3, 1, [0 1]);

bit_I = bit_in(1:2:1e3);

bit_Q = bit_in(2:2:1e3);

data_I = -2*bit_I+1;

data_Q = -2*bit_Q+1;

data_I1=repmat(data_I',20,1);

data_Q1=repmat(data_Q',20,1);

for i=1:1e4

data_I2(i)=data_I1(i);

data_Q2(i)=data_Q1(i);

end;

t=0:0.1:1e3-0.1;

f=0:0.1:1;

xrc=0.5+0.5*cos(pi*f);

data_I2_rc=conv(data_I2,xrc)/5.5;

data_Q2_rc=conv(data_Q2,xrc)/5.5;

f1=1;

t1=0:0.1:1e3+0.9;

I_rc=data_I2_rc.*cos(2*pi*f1*t1);

Q_rc=data_Q2_rc.*sin(2*pi*f1*t1);

QPSK_rc=(sqrt(1/2).*I_rc+sqrt(1/2).*Q_rc);

% 解调

I_demo=QPSK_rc.*cos(2*pi*f1*t1);

Q_demo=QPSK_rc.*sin(2*pi*f1*t1);

I_recover=conv(I_demo,xrc);

Q_recover=conv(Q_demo,xrc);

I=I_recover(11:10010);

Q=Q_recover(11:10010);

t2=0:0.05:1e3-0.05;

t3=0:0.1:1e3-0.1;

data_recover=[];

for i=1:20:10000

data_recover=[data_recover I(i:1:i+19) Q(i:1:i+19)];

end;

ddd = -2*bit_in+1;

ddd1=repmat(ddd',10,1);

for i=1:1e4

ddd2(i)=ddd1(i);

end

figure(1)

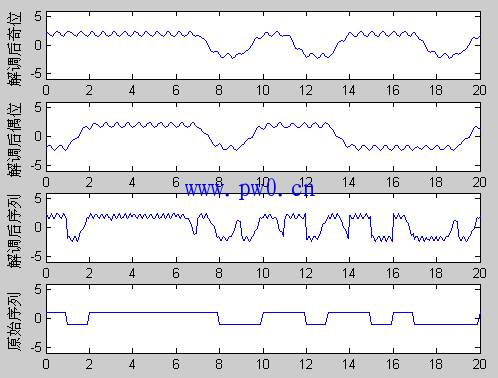
subplot(4,1,1);plot(t3,I);axis([0 20 -6 6]);

subplot(4,1,2);plot(t3,Q);axis([0 20 -6 6]);

subplot(4,1,3);plot(t2,data_recover);axis([0 20 -6 6]);

subplot(4,1,4);plot(t,ddd2);axis([0 20 -6 6]);