了解模型预测控制4--自适应，增益调度和非线性MPC

51 阅读 0 评论 34 点赞

我是靠谱客的博主可耐酸奶，最近开发中收集的这篇文章主要介绍了解模型预测控制4--自适应，增益调度和非线性MPC，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

如果您想使用MPC控制器控制您的系统，但不确定哪些方法可用? 那么，请继续阅读本文章，因为我会给您提供一些方法。

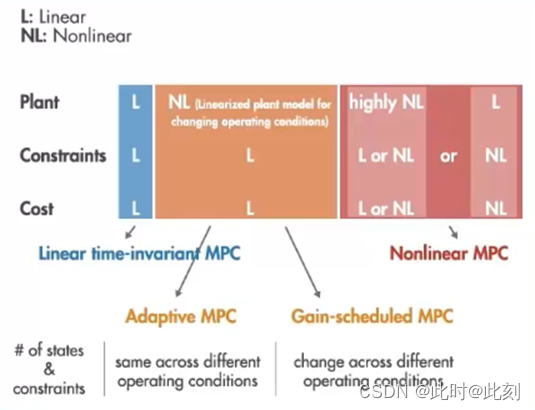
我首先要从煎饼配方开始，如果您耐心等待一会儿，您会看到它与MPC的联系。如果您有面粉、鸡蛋和牛奶，就可以做煎饼，很多人以前都试过这个配方，这很简单，不会出错。同样，如果您有一个由线性被控对象模型表示的线性系统，并且您有线性约束和二次成本函数，那么您可以使用线性时不变 MPC 来控制您的系统。

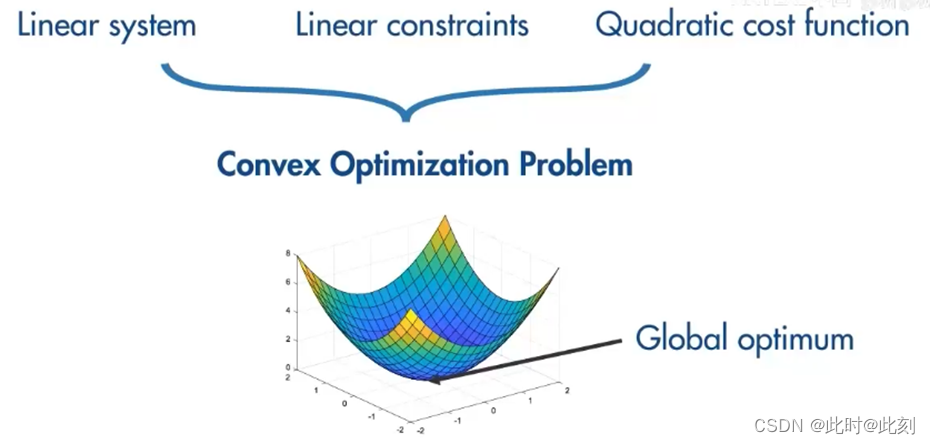
具有这些良好特性的 MPC问题会产生凸优化问题，其中成本函数具有单个全局最优值，而优化的目标是找到这个最优值，这是一个经过充分研究的问题，您可以使用多种数值方法和软件来解决它。

让我们回到煎饼上︰如果您只有杏仁粉而不是面粉怎么办? 还能做煎饼吗?是的，可以! 同样，如果您处理的系统不是线性而是非线性的，您也可以使用线性MPC，并且仍然受益于凸优化问题的良好特性，在这种情况下可用的方法是自适应 MPC 控制器和增益调度MPC 控制器。

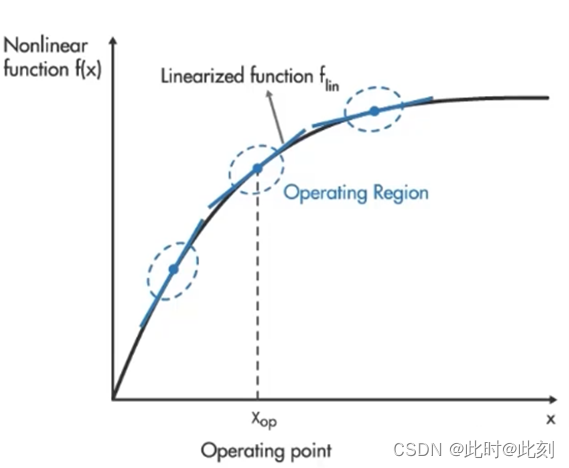
这些控制器处理非线性系统的方式基于线性化。例如，让我们看看这个非线性函数，我们可以在一个工作点对其进行线性化，这为我们提供了一个线性函数，该函数在工作点附近很好地逼近非线性系统，但是，在该区域之外，我们发现的线性函数将无法正常工作。因此，我们通常感兴趣的是找到多个线性化模型，每个模型都能很好地表示其工作点附近的非线性函数。

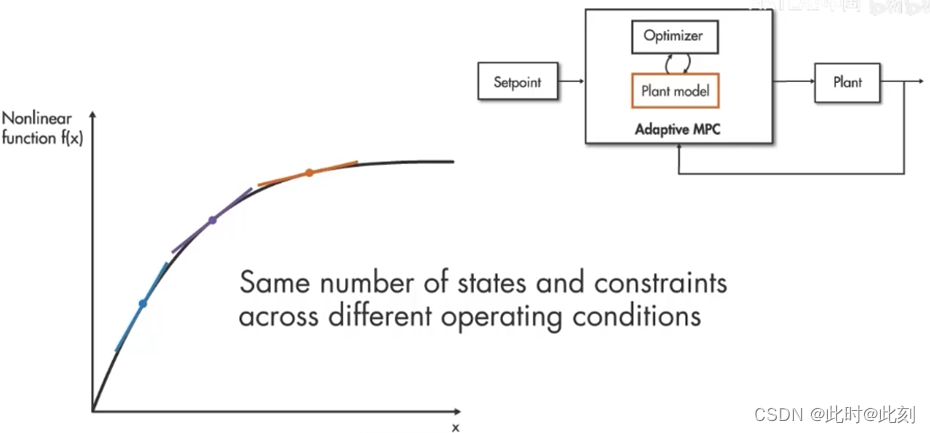
这是我们之前讨论过的常规 MPC 控制图（如下图所示），它使用内部被控对象模型和优化器来计算控制动作。在自适应MPC 中，线性模型是随着工作条件的变化而动态计算的，并且在每个时间步长，您都可以使用此线性模型更新。MPC控制器使用的内部被控对象模型，请注意，在自适应MPC 中，优化问题的结构在不同的工作点上保持不变。这意味着在预测范围内，状态数量和约束数量不会因不同的操作条件而改变。

但是，如果它们确实发生了变化，则应使用增益调度MPC。在增益调度MPC 中，您可以在感兴趣的工作点进行离线线性化，并为每个工作点设计一个线性MPC控制器。每个控制器彼此独立，因此可能具有不同数量的状态和不同数量的约束。请注意，在这种方法中，您还需要设计一种算法，针对不同的工作条件在预定义的 MPC控制器之间进行切换。

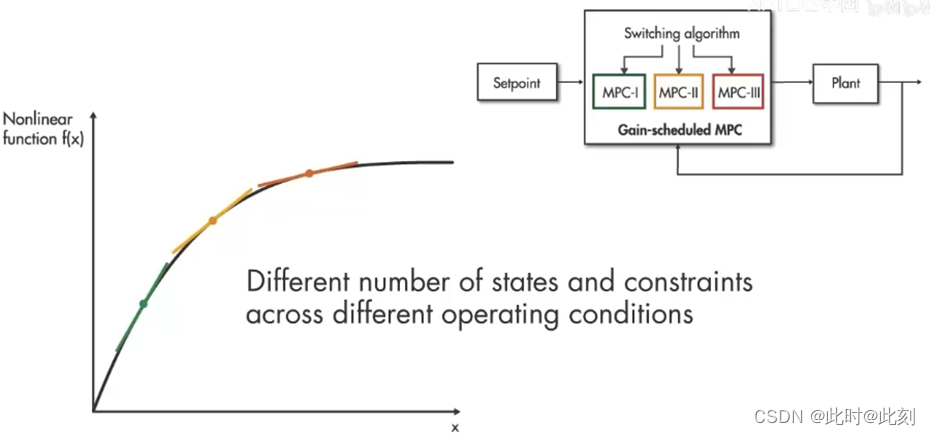
尽管拥有独立控制器是增益调度 MPC的一个优势，但它使用的内存要比自适应 MPC多。因此，如果可以在运行时找到线性被控对象模型，并且优化问题的结构在不同的工作条件下保持不变，建议使用自适应MPC。如果结构发生变化，则可以使用增益调度MPC，通过设计独立的MPC控制器来适应不断变化的工作条件。

现在让我们再次回到煎饼。假设您没有用来烘焙的常规食材，但有一些您甚至都不熟悉的非常独特的原料，用这些原料制作煎饼会颇具挑战性，但一旦您知道怎么做，它将是有史以来最好吃的煎饼。如果您有一个非线性系统不能用线性模型很好地逼近，那么您可以使用非线性 MPC。这是最有效的方法，因为它使用最准确的被控对象表示，即非线性被控对象模型，因此，控制器做出的预测更准确，这也会实现更好的控制动作。

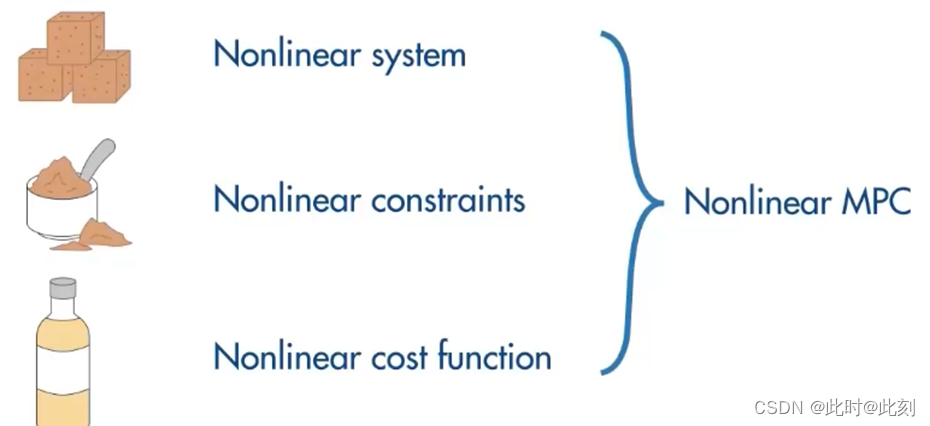
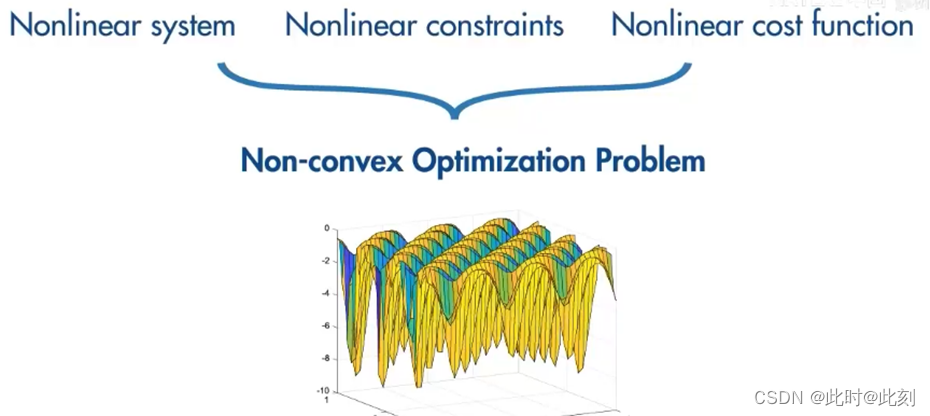
但是，它在实时求解方面最具挑战性，因为当您有非线性约束和非线性成本函数时，优化问题就变得非凸了，成本函数可能有多个局部最优解，找到全局最优解可能很困难。对需要大量计算的非凸优化问题的求解效率，取决于您拥有的非线性求解器。

总而言之，如果您处理的被控对象是非线性的，但可以通过线性模型逼近，则可以使用自适应MPC 控制器和增益调度 MPC 控制器。如果优化问题的结构在不同的工作条件下没有变化，则应使用自适应 MPC；但是，如果该结构有变化，则使用增益调度 MPC；如果因您有一个无法通过线性化进行良好逼近的高度非线性系统，从而导致以上这些方法都不起作用，则可以使用非线性MPC。