音频信号处理笔记（一）01 信号的时域分析

63 阅读 0 评论 42 点赞

我是靠谱客的博主伶俐信封，最近开发中收集的这篇文章主要介绍音频信号处理笔记（一）01 信号的时域分析，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

相关课程：【音频信号处理及深度学习教程】

文章目录

0
1 信号的时域分析
- 1.1 分帧
- - 1.1.1 幅值包络
  - 1.1.2 均方根能量

0

信号的叠加：https://teropa.info/harmonics-explorer/

一个复杂信号分解成若干简单信号分量之和。不同个频率信号的叠加: 由于和差化积，会形成包络结构与精细结构。

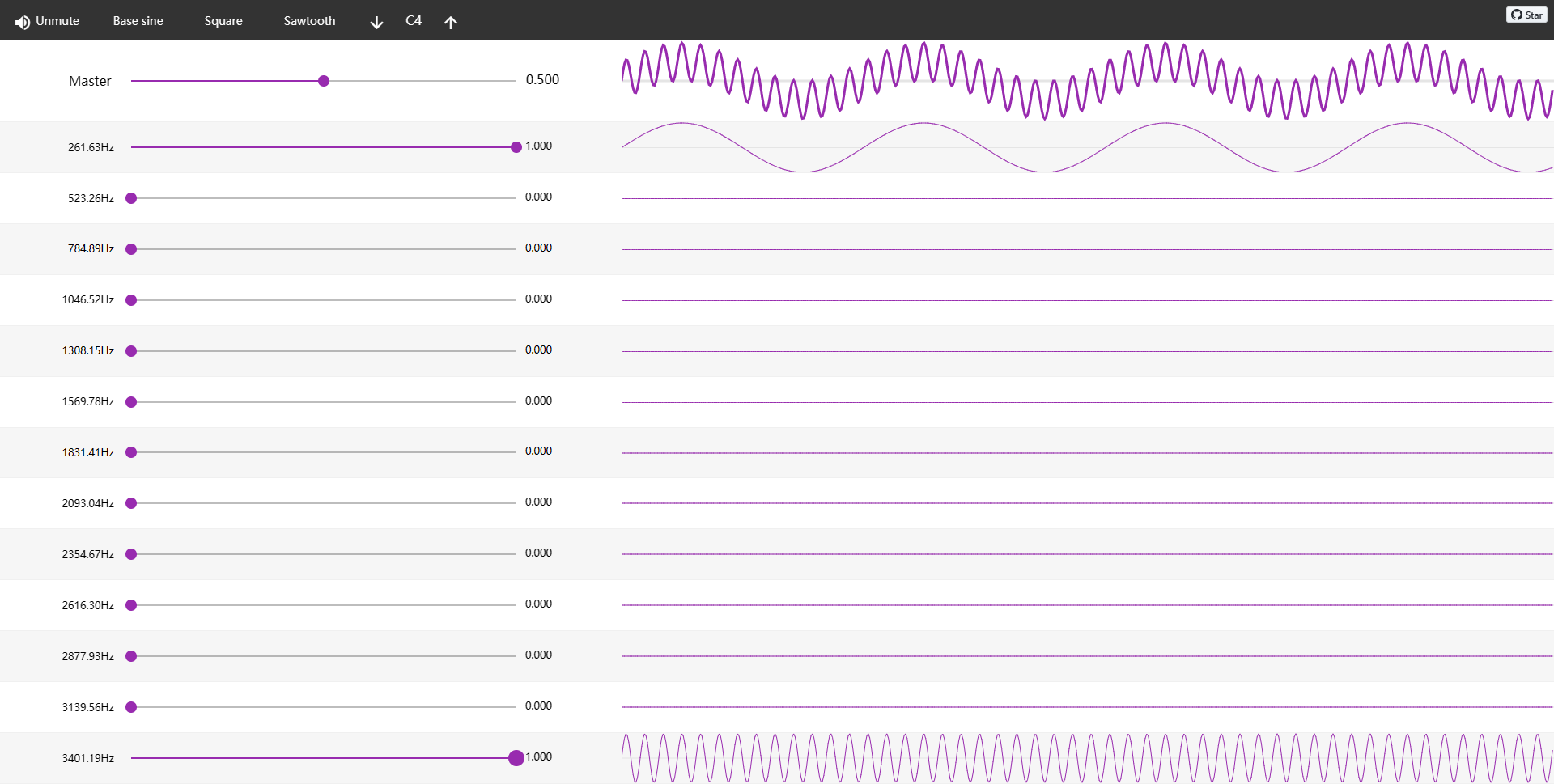
由上图可知，低频信号决定了信号的包络形状,高频信号决定其精细结构。

在语音识别中,主要通过信号的包络结构来区分不同音频信号,因此在识别领域更关注低频作用

1 信号的时域分析

1.1 分帧

分帧：将信号按照时间尺度分割，每一段的长度就是长frame_size，分出n段，为的个数frame_num，如果不考虑重叠分帧，那么该信号总的采样点数为frame_size * frame_n um。

分帧重叠：为了让分后的信号更加平滑，需要重叠分帧，也就是下一帧中包含上一帧的采样点，那么包含的点数就是重叠长度hop_size。

分帧补零：帧的个数frame_num= 总样本数N / 重叠数hop_size(分不补零)，因为的个数frame_num是整数为了不舍弃最后一帧不能凑成一个完整长的点，需要对信号补零。此时帧的个数frame num =(总样本数N - 帧长frame size)/ 重叠数hop _size(分补零)+1

1.1.1 幅值包络

幅值包络：依次寻找每一帧的幅值最大值，将每一帧中幅值最大值连起来就是幅值包络（响度、音频检测、音频分类）

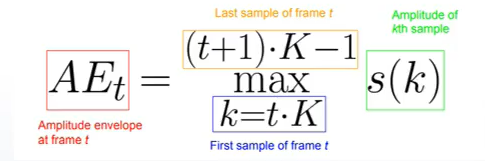
现提取第t帧的AE值，其中k是采样点数，t是序列数，K是每一帧的帧长，采样点k点在t k,(t+1) k-1

代码如下：

import librosa
import numpy as np
import librosa.display
from matplotlib import pyplot as plt

wave_path_absolute = r"E:VoiceDevaudio_datamusic_piano.wav"
wave_path = "../audio_data/music_piano.wav"
# 1. 加载信号以及采样率
waveform, sample_rate = librosa.load(wave_path_absolute, sr=None)


# 2. 定义AE函数，功能是取信号每一帧中幅值最值为该帧的包络
# 信号，每一帧长，重叠长度
def Calc_Amplitude_Envelope(waveform, frame_length, hop_length):
    # 如果按照帧长来分割信号，余下部分不能形成一个帧则需要补0
    if len(waveform) % hop_length != 0:
        # ?
        frame_num = int((len(waveform) - frame_length) / hop_length) + 1
        pad_num = frame_num * hop_length + frame_length - len(waveform)  # 补0个数
        waveform = np.pad(waveform, pad_width=(0, pad_num), mode="wrap")  # 补0操作

    frame_num = int((len(waveform) - frame_length) / hop_length) + 1
    waveform_ae = []
    for t in range(frame_num):
        current_frame = waveform[t * (frame_length - hop_length):t * (frame_length - hop_length) + frame_length]
        current_ae = max(current_frame)
        waveform_ae.append(current_ae)
    return np.array(waveform_ae)


# 3. 设置参数：每一帧长1024，以50%的重叠率分帧，调用该函数
frame_size = 1024
hop_size = int(frame_size * 0.5)
waveform_AE = Calc_Amplitude_Envelope(waveform=waveform, frame_length=frame_size, hop_length=hop_size)

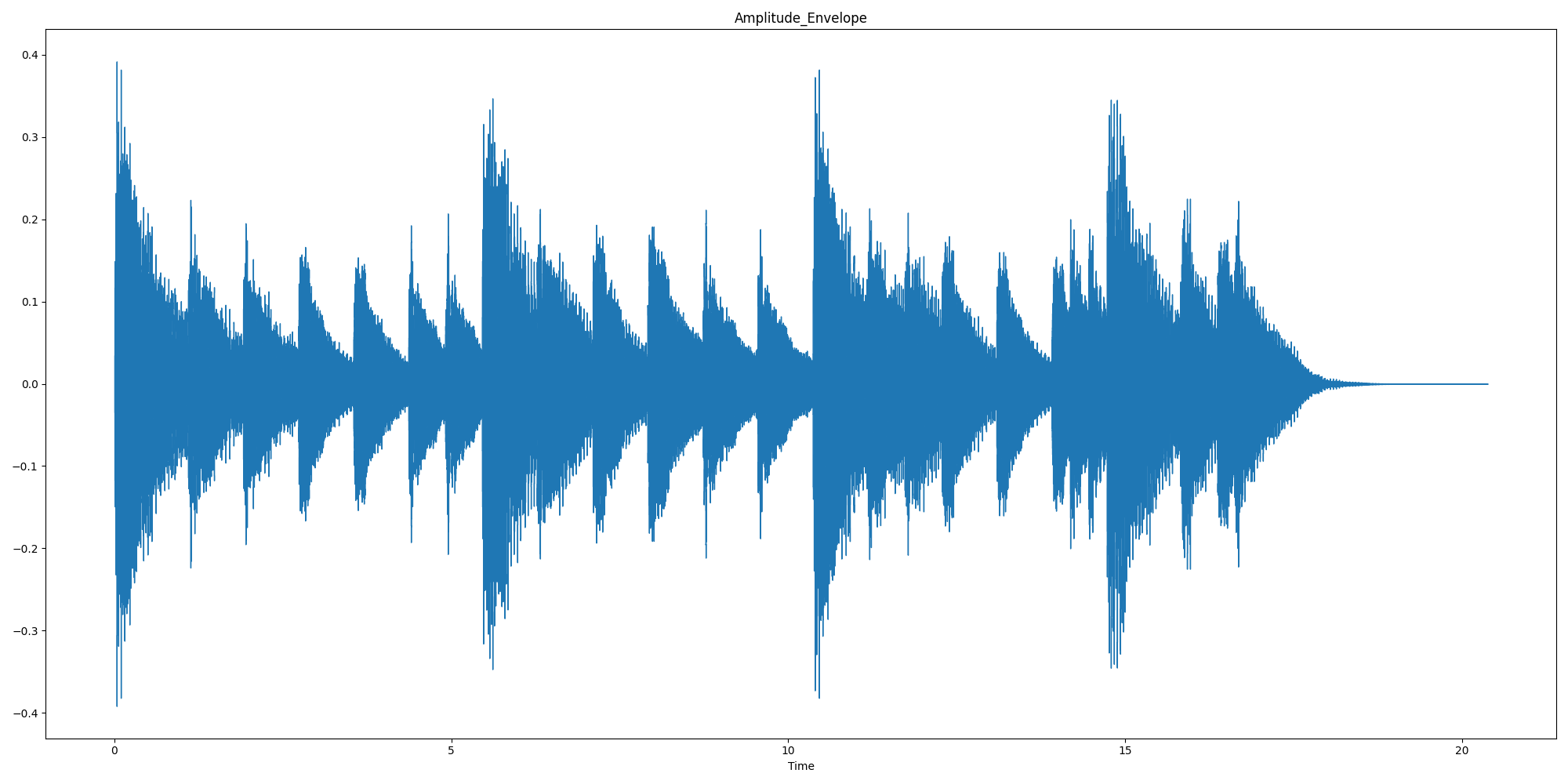
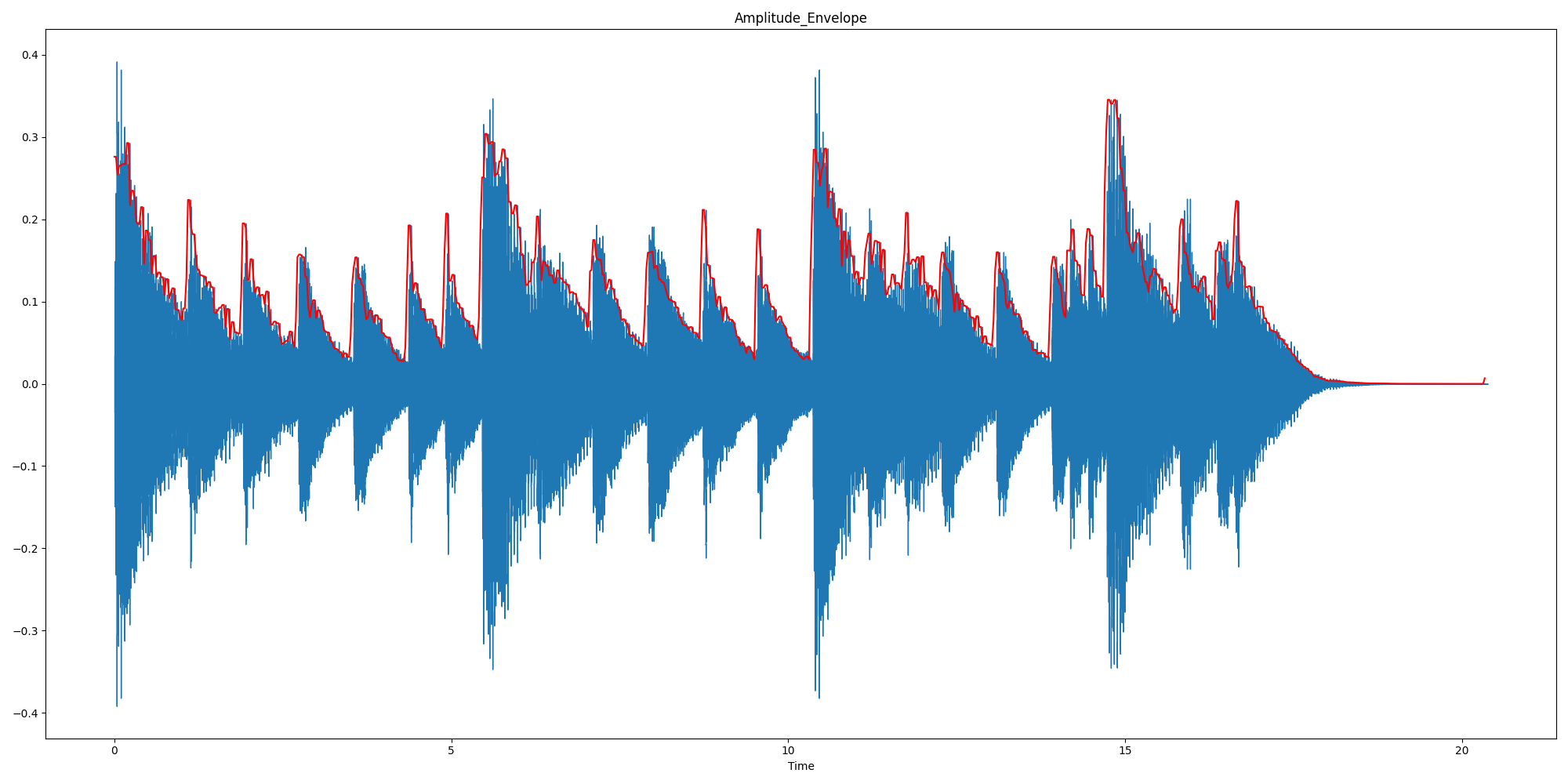
# 4.绘制信号的幅值包络信息
frame_scale = np.arange(0, len(waveform_AE))
time_scale = librosa.frames_to_time(frame_scale, hop_length=hop_size)
plt.figure(figsize=(20, 10))
librosa.display.waveshow(waveform)
plt.plot(time_scale, waveform_AE, color='red')
plt.title("Amplitude_Envelope")
plt.show()

1.1.2 均方根能量

均方根能量（Root mean square energy）（响度、音频分段分类）

依次寻找每一帧中的RMSE，它的值为第t帧中每点幅值平方再取均值后开根号

代码如下：

# 0. 预设环境
import librosa
import numpy as np
from matplotlib import pyplot as plt
import librosa.display

# 1.加载信号
wave_path_absolute = r"E:VoiceDevaudio_datamusic_piano.wav"
wave_path = "../audio_data/music_piano.wav"
waveform, sample_rate = librosa.load(wave_path_absolute, sr=None)

# 2.定义函数RMS，功能：计算每一帧的均方根能量
def Calc_RMS(waveform, frame_length, hop_length):
    # 如果按照帧长来分割信号，余下部分不能形成一个帧则需要补0
    if len(waveform) % hop_length != 0:
        # ?
        frame_num = int((len(waveform) - frame_length) / hop_length) + 1
        pad_num = frame_num * hop_length + frame_length - len(waveform)  # 补0个数
        waveform = np.pad(waveform, pad_width=(0, pad_num), mode="wrap")  # 补0操作

    frame_num = int((len(waveform) - frame_length) / hop_length) + 1
    waveform_rms = []
    for t in range(frame_num):
        current_frame = waveform[t * (frame_length - hop_length):t * (frame_length - hop_length) + frame_length]
        current_rms = np.sqrt(np.sum(current_frame**2) / frame_length)
        waveform_rms.append(current_rms)
    return waveform_rms

# 3. 设置参数：每一帧长1024，以50%的重叠率分帧，调用该函数
frame_size = 1024
hop_size = int(frame_size * 0.5)
waveform_RMS = Calc_RMS(waveform=waveform, frame_length=frame_size, hop_length=hop_size)

# 4.绘制图像
frame_scale = np.arange(0, len(waveform_RMS), step=1)
time_scale = librosa.frames_to_time(frame_scale, hop_length=hop_size)
plt.figure(figsize=(20, 10))
plt.plot(time_scale, waveform_RMS, color='red')
plt.title("Root-Mean-Square-Energy")
librosa.display.waveshow(waveform)
plt.show()

# 5. 利用librosa.feature.rms绘制信号的RMS
waveform_RMS_librosa = librosa.feature.rms(y=waveform, frame_length=frame_size, hop_length=hop_size).T[1:,0]
plt.figure(figsize=(20, 10))
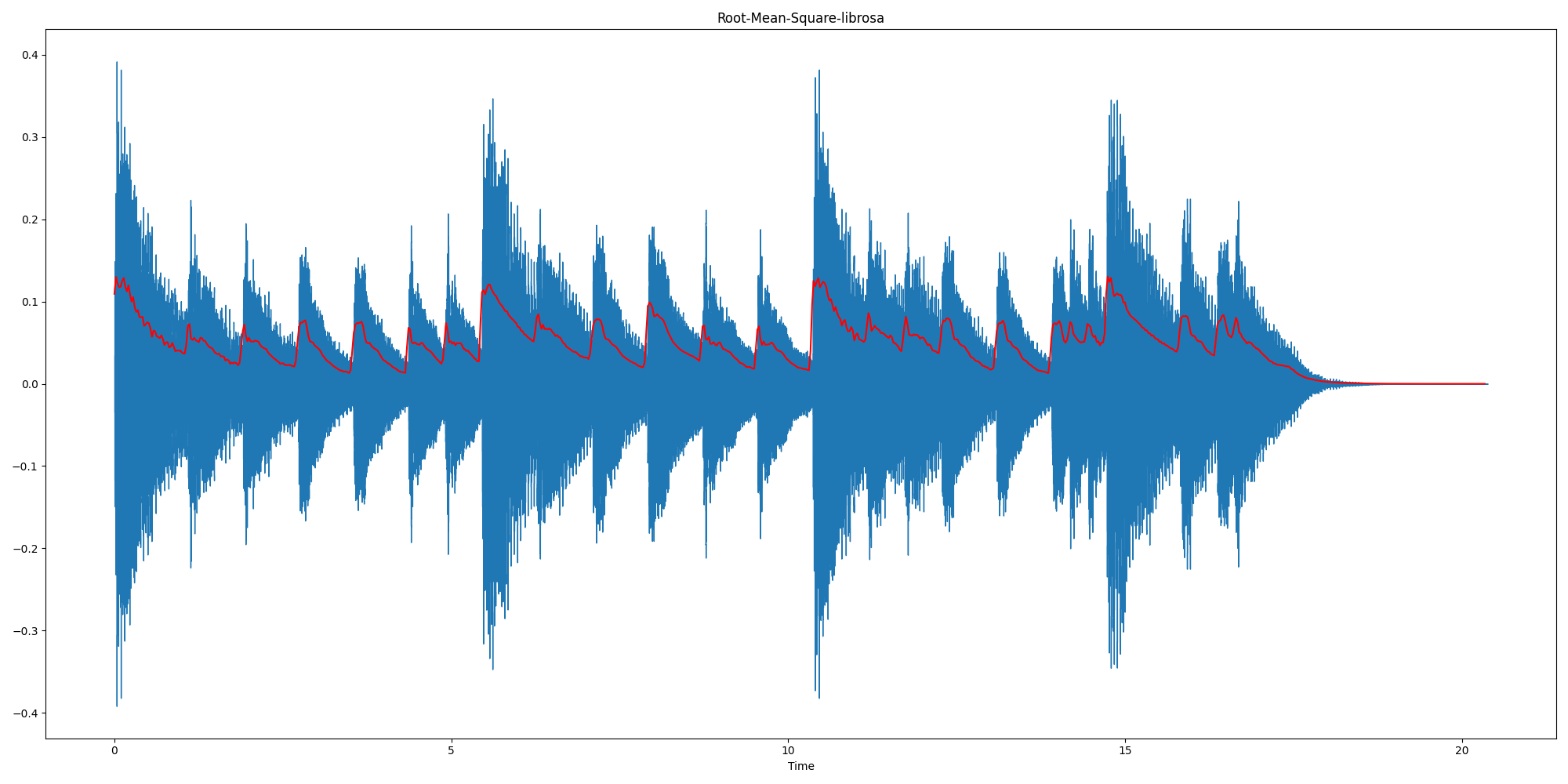
plt.plot(time_scale, waveform_RMS_librosa, color='red')
plt.title("Root-Mean-Square-librosa")
librosa.display.waveshow(waveform)
plt.show()

bias = waveform_RMS_librosa - waveform_RMS
print(f"the bias is {bias}n Congratulation!")