SHARC音频DSP的算法详解（二）数字信号的时域及频域分析方法

作者的话

多年前参加ADI SHARC L2培训的时候，获得的干货，分享给大家。讲算法的很多，讲SHARC DSP算法的就几乎没看到，那你就跟着我往下看，后面的文章都是讲SHARC的算法，我截取一下，结合一点点自己的理解，转述给大家。

硬件准备

ADSP-21489EVB：ADI 21489 DSP的开发板

AD-HP530ICE：ADI DSP通用仿真器

软件准备

Visual DSP++：ADI DSP的软件开发环境

数字信号的时域及频域分析方法

1. 时域

（1）卷积

设系数的单位脉冲响应为 h(n), 输入信号为 x(n), 则其输出信号 y(n)可以通过以下卷积公式来实现：

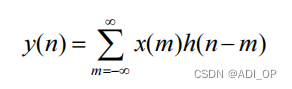
Matlab 实现函数：y = conv(x, h)

（2）差分方程

系统的输入输出还可以用下面的方程来描述，这种方程在数字信号处理中称为差分方程。

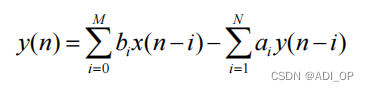
上式中，若 i>=1 时，ai = 0，则此差分方程描述的是一个 FIR 系统，否则为一个IIR 系统。设计一个滤波器其实就是根据所需的指标设计差分方程的系数 bi, ai。

Matlab 实现函数：y = filter(B, A, x), 其中 B=[b0, b1, …, bM], A=[1, a1,…, aN].

（3）滤波器的网络结构

用不同的方法可以将上述的差分方程排列成不同的等效差分方程组，每组都有自己具体的计算过程（或算法）。每一种具体的算法都可以由延时器、乘法器、加法器组成方框图来实现。

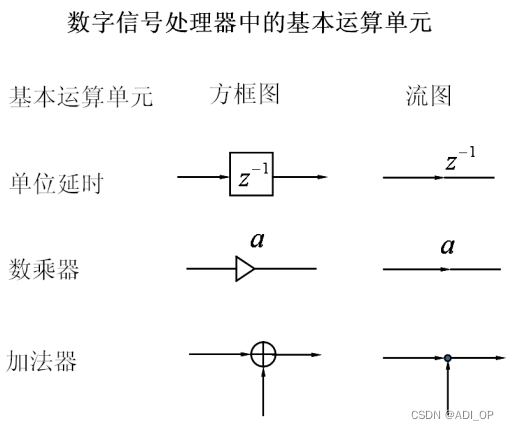
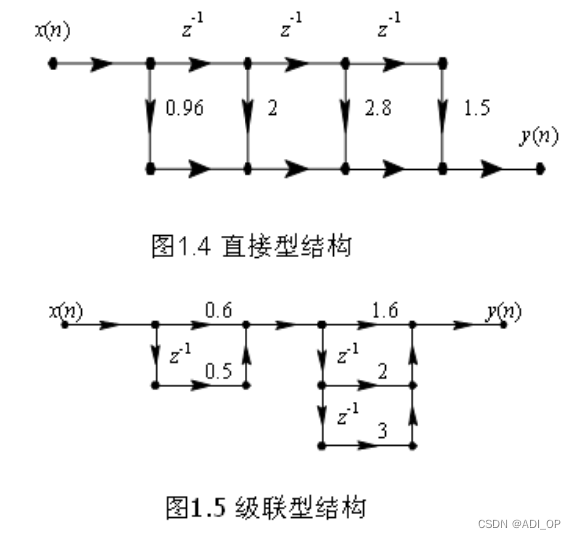
例如：

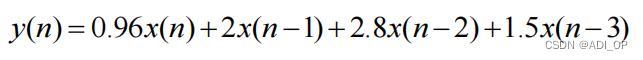
可分别由图 1.4 的直接型结构, 图 1.5 的级联型结构来实现。

2. 频域

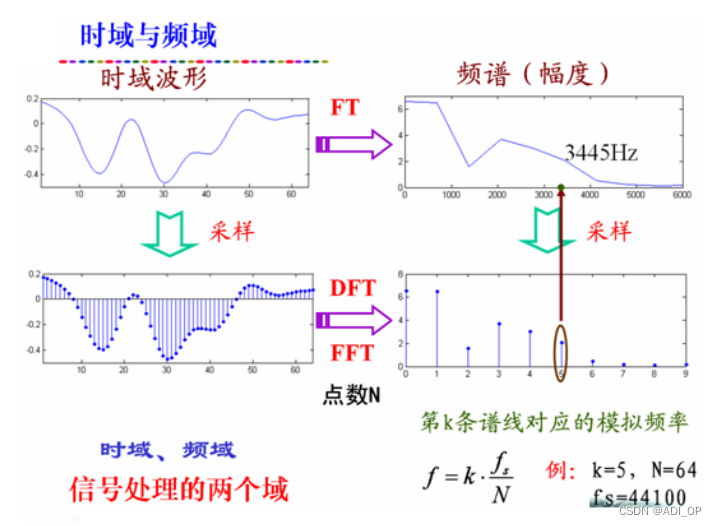
（1）数字频率与模拟频率的关系

设采样率为 fs, 某信号的模拟频率为 f(Hz), 则其数字域频率为：

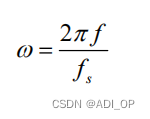
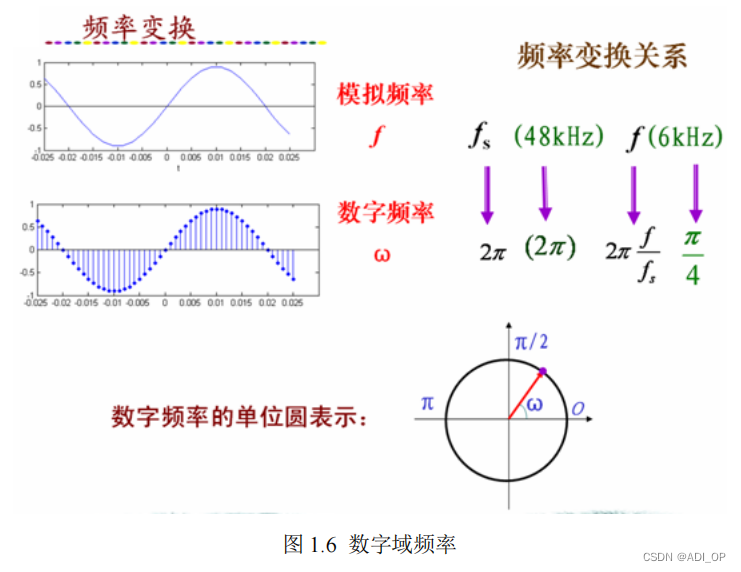
图 1.6 是模拟频率与数字频率变换的示意图。

（2）z 变换

z 变换是对信号和系统进行分析的重要数学工具，许多问题用 z 变换进行分析和求解很方便，概念清楚。

设输入信号为 x(n)，则对应的 z 变换是：

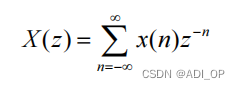
若输入信号为 x(n-n0)，则对应的 z 变换是:

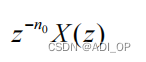
若系统的单位脉冲响应为 h(n), 则系统函数是：

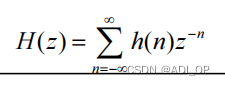
或根据系统的差分方程也能得到系统函数：

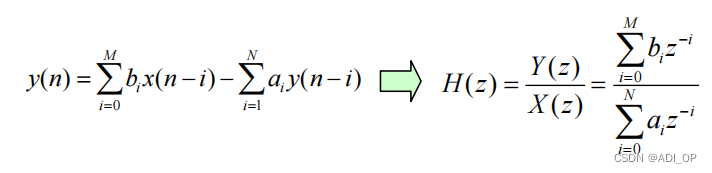
将 H(z)写成下式的形式：

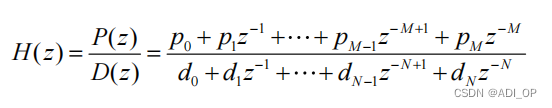
分子多项式的根：零点
分母多项式的根：极点
要使系统稳定，必须保证极点 zk 满足 |zk|< 1。

（3）傅里叶变换

傅里叶变换把信号从时间域转换到实频域，而 z 变换作为傅里叶变换的推广，将信号从时间域转换到复频域。单位圆上的 z 变换即为傅里叶变换。

时域离散信号的傅里叶变换公式：

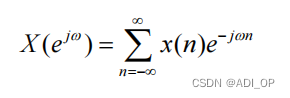
这个公式虽然可以将信号从时域变换到频域，但其结果是连续函数，无法用数字系统进行处理。离散傅里叶变换（DFT）的结果是对上述频谱结果等间隔采样，使得频域函数也被离散化了，使数字信号的处理也可以在频域用数字系统进行处理。

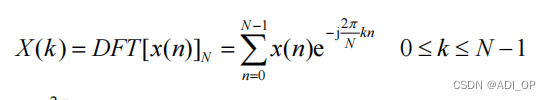
一般令

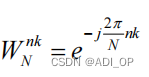
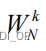
称为旋转因子。

DFT 使数字系统在频域处理信号成为可能，但是当 N 很大时，直接计算 N 点 DFT的计算量非常大，计算 N 个点的 DFT 所需的计算量为：复数加法 N(N-1)，复数乘法N 2，运算量大，与 N 2 成正比。通过 FFT 则可以降低运算量，特别是 N 越大，效果越明显，从而使数字信号处理的速度大大提高。

FFT 的思路：将长序列 DFT 分解为短序列的 DFT；利用旋转因子 的周期性、对称性。

最常用的 FFT 算法是基 2 时间抽取(Decimation in time)DIT-FFT 算法，将时域序列按奇偶逐次分解为两组子序列，利用旋转因子的特性，由子序列的 DFT 来实现整个序列的 DFT。

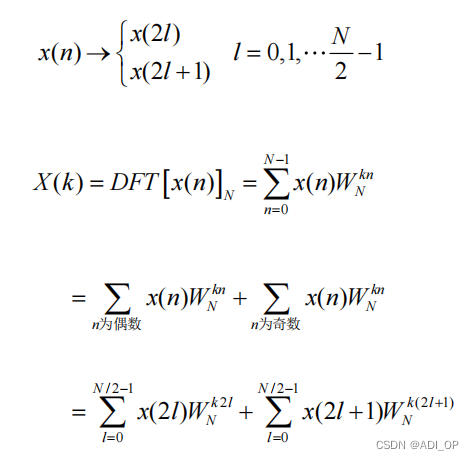
令:

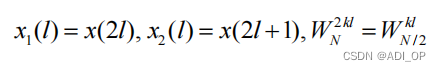
N为2的整数倍.

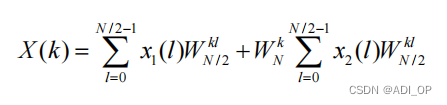
分解为 2 个 DFT：

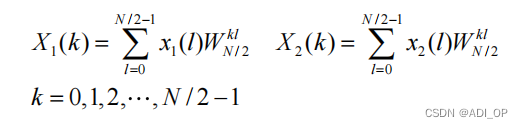
以下为 8 点 DIT-FFT 运算流图：

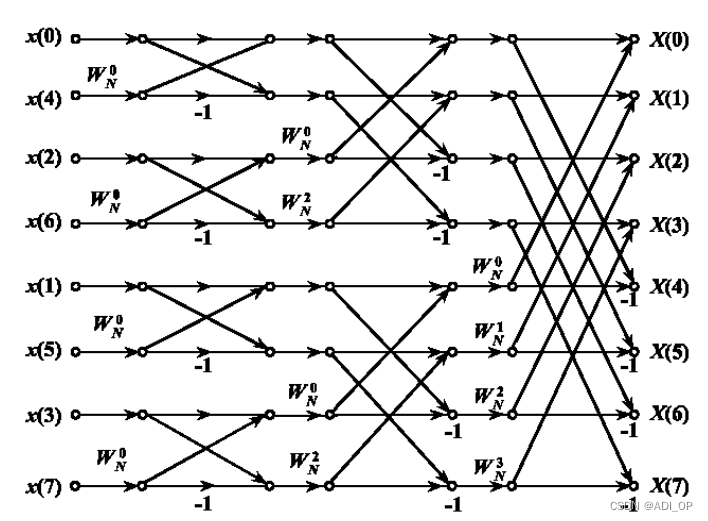
DIT-FFT 的运算量：

（4）数字域与模拟域小结

最后

以上就是威武茉莉为你收集整理的SHARC音频DSP的算法详解（二）数字信号的时域及频域分析方法的全部内容，希望文章能够帮你解决SHARC音频DSP的算法详解（二）数字信号的时域及频域分析方法所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。