heun 方法 matlab代码_MATLAB中代码优化的两种方法MATLAB中的代码优化小结

95 阅读 0 评论 63 点赞

我是靠谱客的博主光亮小蝴蝶，最近开发中收集的这篇文章主要介绍heun 方法 matlab代码_MATLAB中代码优化的两种方法MATLAB中的代码优化小结，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

MATLAB中的代码优化

MATLAB中的代码优化有两种重要的方法：预分配组和向量化循环。

我们举一个简单的例子来看，创建一个MATLAB函数来计算f(x) = sin(x / 100π)：

function y = sinfun1(M)
x = 0: M - 1;
for k = 1: numel(x)
    y(k) = sin(x(k) / (100 * pi));
end

这里我们使用函数timeit来计算调用函数所需的时间。(timeit可用于得到函数调用的可靠的、可重复的时间测量。)

此时我们得到M数量级为20000时的时间测量，如图1所示：

图1 函数sinfun1在M=20000的时间测量

我们在编写完函数sinfun1后可以看到MATLAB编辑器给出了一个提示：变量’y’似乎会随迭代次数而改变，请预分配内存以获得更高的运算速度。

为什么会出现这样的情况？那是因为在sinfun1这个函数中，输出变量y每经过一次循环后都会增长一个元素大小，它必须重新分配新的存储空间，并且在每次数组生长时都要复制前一组数组元素。这种频繁的内存重新分配和复制的开销非常大，与sin本身的计算相比需要更多的时间。

此时我们采用预分配数组的办法进行尝试：

预分配组：是指在进入一个计算数组元素的for循环之前，初始化数组。预分配就意味着咋循环开始之前把它初始化为所希望的输出大小。

function y = sinfun2(M)
x = 0: M - 1;
y = zeros(1, numel(x));
for k = 1: numel(x)
    y(k) = sin(x(k) / (100 * pi));
end

在这里我们使用了zeros生成一个矩阵来预分配存储空间，然后调用timeit计算M=20000时候的时间测量，如图2：

图1 函数sinfun2在M=20000的时间测量

通过对比可以得出，在M=20000的数量级下，使用预分配数组的办法，要比不使用运行快4倍。接下来我们在M的数量级为200000和2000000下对两种方法进行比较，得出的结果如图3，图4所示：

图3 两种方法在M=200000下的时间测量

图4 两种方法在M=2000000下的时间测量

我们通过计算可以得出，函数sinfun1基本维持了所要求的的时间与M成正比，sinfun2则在数量级到了一定程度后维持正比。另外比较两个函数在200000和2000000下的速度比，可见在这两个数量级下预分配数组的方法大约要比sinfun1快6倍。

向量化循环是指使用矩阵/向量运算符、索引技术和现有的MATLAB或工具箱函数来完全消除循环的一种技术。

我们使用向量化循环对矩阵的输入进行逐元素的操作来消除循环：

function y = sinfun3(M)
x = 0: M - 1;
y = sin(x ./ (100 * pi));
end

此时我们再用timit在M=20000时进行时间测量，如图5：

图5 函数sinfun3在M=20000的时间测量

由图可知我们使用向量化时，在M=20000时要比预分配数组快3倍。接下来测量M的数量级为200000和2000000的时间。如图6所示：

图6 函数sinfun3在M=200000和2000000的时间测量

由此可见，不带循环sinfun3的执行速度和带一个循环的sinfun2的执行速度大致相同，但又略快于sinfun2。在教材中为了为了更好地说明这个比较两种优化方法，给出了下面这个例子。

这个例子是基于公式f(x) = Asin(u0x + v0y)创建一幅合成图像，首先使用嵌套的for循环来计算f：

function f = twodsin1(A, u0, v0, M, N)
%f = zeros(M, N);
for c = 1 : N
    v0y = v0 * (c - 1);
    for r = 1 : M
        u0x = u0 * (r - 1);
        f(r, c) = A * sin(u0x + v0y);
    end
end

不使用预分配和使用后的执行时间如图7所示：

图7 函数twodsin1使用预分配的前后比较

我们在这里发现使用预分配前后，执行时间的差距并没有很大。接下来来看向量化后的结果。

在实验中使用一个meshgrid的MATLAB函数将函数重写为没有for循环的形式。

function f = twodsin2(A, u0, v0, M, N)
r = 0 : M - 1;
c = 0 : N - 1;
[C, R] = meshgrid(c, r);
f = A * sin(u0 * R + v0 * C);

继续用timeit测试，得到的结果如图8：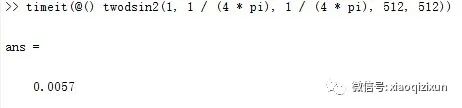

图8 函数twodsin2的时间测量

可见使用向量化后，比使用预分配快了30%，比不使用任何优化方法快了50%。

小结

综合以上两个实验表明，两种代码优化方法(预分配数组和向量化循环)在具体的使用中的差别并不是很大，都可以提升循环运行的速度。我们可以在遇到具体问题后，根据具体情况选择具体的方法：若是循环存在没有预分配内存的问题，那我们可以考虑采用预分配的方法，这样对代码的改动不大，更直观，也更容易表示我们代码得到实际工作机理；若是确定没有预分配的问题，就可以选择向量化循环的办法，这样与基于循环的代码相比，向量化后的代码更易于阅读，更为简洁。