从正弦波转换为方波

此示例说明方波的傅里叶级数展开式是如何由奇次谐波的和构成的。

首先以 0.1 为步长，生成一个从 0 到 10 的时间向量，并求出所有点的正弦。绘制基频图。

t = 0:.1:10;
y = sin(t);
plot(t,y);

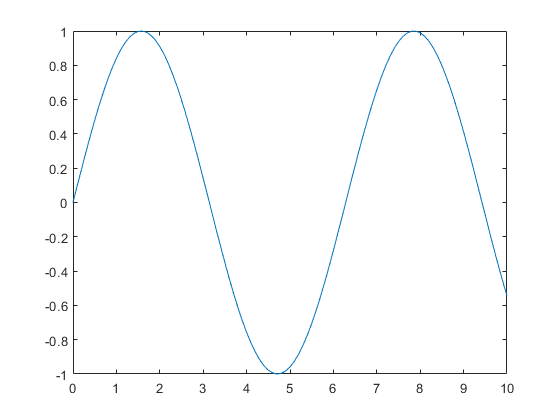
接下来，向基频添加第三个谐波，并绘制谐波图。

y = sin(t) + sin(3*t)/3;
plot(t,y);

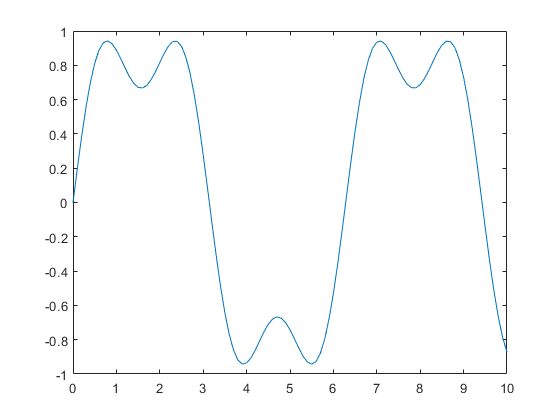
接下来使用第一、第三、第五、第七和第九个谐波。

y = sin(t) + sin(3*t)/3 + sin(5*t)/5 + sin(7*t)/7 + sin(9*t)/9;
plot(t,y);

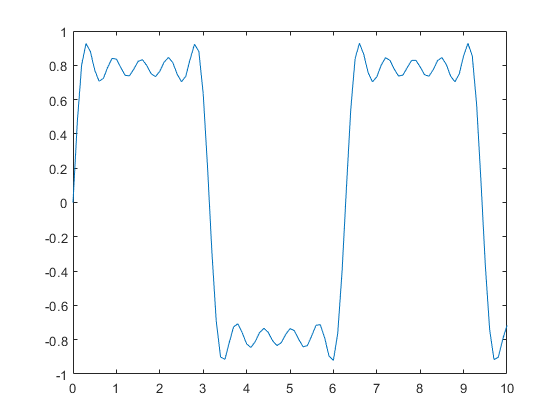
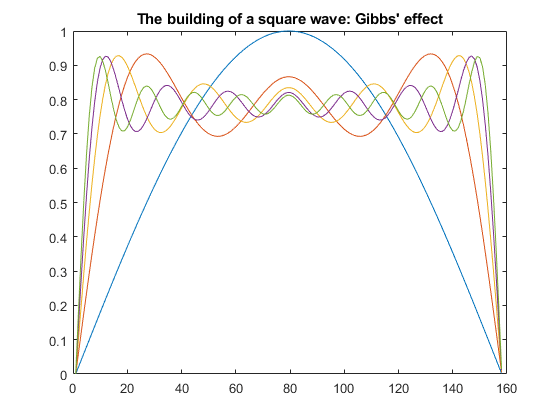
最后，从基频开始创建更多连续谐波的向量，一直到第 19 个谐波为止，并将所有中间步长保存为矩阵的行。

在同一个图窗中绘制这些向量，以便显示方波的演变。请注意，吉布斯效应表明它实际上永远不会转换为方波。

t = 0:.02:3.14;
y = zeros(10,length(t));
x = zeros(size(t));
for k = 1:2:19
   x = x + sin(k*t)/k;
   y((k+1)/2,:) = x;
end
plot(y(1:2:9,:)')
title('The building of a square wave: Gibbs'' effect')

下面提供了一个三维曲面图，该曲面图表示正弦波到方波的逐变过程。

surf(y);
shading interp
axis off ij

最后

以上就是坚定香氛为你收集整理的从正弦波转换为方波的全部内容，希望文章能够帮你解决从正弦波转换为方波所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。