一、实验目标
1、以某韵母和某清音声母为分析对象,求其短时自相关函数(不用xcorr)和短时平均幅度差函数,比较清浊音;
2、计算改进的短时自相关函数和改进的短时平均幅度差函数,比较改进前后的差异(以韵母为例);
3、用改进后的短时自相关法和短时平均幅度差估计韵母的基频数值并将其基频曲线画出来,加入三电平削波和中值平滑;
4、将自己两种方法的结果与praat求得的结果相比较(两者的帧长帧移等数值要设置成一样的)
5、用matlab编写代码并做好word文档。
二、实验原理
(一)短时自相关函数
一般情况下,相关函数用于测定两个信号在时域内的相似程度。自相关函数主要研究信号本身的同步性和周期性。
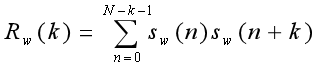
1、是偶函数,k的取值从0到N-1;
2、s(n)是周期的,那么R(k)也是周期的;
3、k = 0处最大值,对所有k来说,|R(k)|≤R(0),可用于基音周期估计和线性预测分析;
窗函数长度至少大于两个基音周期才会有好效果,否则找不到最大值点。但是也不要太大,否则影响短时性。
(二)修正的自相关函数
基音周期范围很宽,所以要预估合适的窗长并不容易。为此可采用基于基音周期的自适应窗口长度法,修正短时自相关函数。
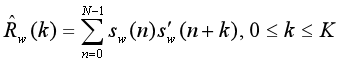
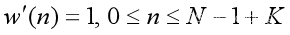
因为求和上限是N-1,与k无关,故当k增加时,Rn(k)值不下降 。
采用修正的自相关函数后,窗长的变小,不会影响到基音周期附近最大值的出现
(三)短时平均幅度差函数(AMDF)
为了避免短时自相关函数计算时大量乘法运算,使用有相似作用的另一参量简化运算,即短时平均幅度差函数(AMDF)。它是基于以下想法:对一个周期为P的信号做差值,即有d(n) = x(n)–x(n-k)
则在k等于P的整数倍时上式即为0。即k与周期吻合时,d的短时平均幅度值总是很小。因此定义AMDF为:
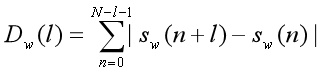
对于周期性信号,AMDF也呈现周期性。不过,它在周期整数倍点上是谷值,而不是峰值。
(四)短时参数上的基音周期估计
方法一;
1,1 kHz以下低通滤波;
2,2 kHz重采样;(downsample,resample)
3,分帧,用自相关或AMDF法提取基频;
4,平滑处理
方法二:
1,中心削波(分帧前或者后都可以);
2,用自相关法或者AMDF方法提取基频;
3,平滑处理
提取的基音频率轨迹与真实轨迹不可能完全吻合,局部段落和区域有一个或几个基音频率估计值偏离,这种偏离点为基音轨迹的“野点”。野点的存在会严重干扰最终结果,所以要进行诸如滤波、中心削波、平滑这些处理。
削波后的序列用短时自相关函数估计基音周期,在基音周期处峰值更加尖锐, 可减少倍频或半频错误。中心削波函数为:
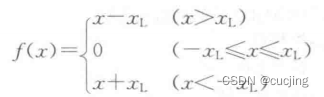
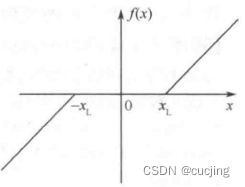
为克服短时自相关函数计算量大的问题,还可采用三电平削波法,削波后序列仅有1,0,-1三种取值,求自相关就无需乘法运算。三电平削波函数为:
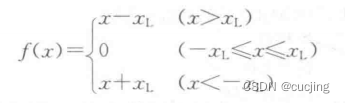
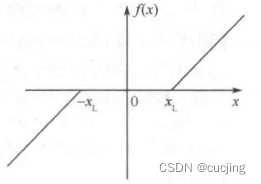
估计值常出现偏离正常的结果,可以进行平滑处理,除去野点,避免平滑段之间的阶跃变化:中值平滑、线性平滑、组合平滑
中值平滑处理基本原理:采用一个滑动窗,中心在Xn处,左右各取L个点,共2L+1个样本,将其按大小顺序排列,取其中间值作为平滑器的输出y。L一般取1或者2,那么窗口套住的样本就是3个和5个,称为3点或者5点中值平滑。其优点是既可以有效消除少量野点,还不会破坏数据在两个平滑段之间的阶跃性变化。
三、实验程序和分析
(一)韵母a和清音声母s的短时自相关函数和短时平均幅度差函数
[y,fs] = audioread('a.wav');%读出信号
y1=filter([1 -0.98],1,y);%预加重
N=length(y1);
%加窗分帧处理
len=200; % 帧长
inc=100; % 帧移
win=boxcar(len); %生成长度为len的矩形窗
y2=enframe(y1,win,inc)'; % 按照帧长和帧移进行分帧,分帧后的数组(帧长×帧数)
x=y2(:,i); %获取某一帧的数据
%短时自相关函数
for k=1:len
R(k)=sum(x(k:end).*x(1:end-k+1));
end
%短时平均幅度差函数
for m=1:len
amdfvec(m) = sum(abs(x(m:end)-x(1:end-m+1))); % 求每个样点的幅度差再累加
end
subplot(1,2,1); %短时自相关函数
plot(R);
title('短时自相关函数');
ylabel('幅值');
xlabel('样点' );
subplot(1,2,2); %平均幅度差函数
plot(amdfvec);
title('平均幅度差函数');
ylabel('幅值');
xlabel('样点' );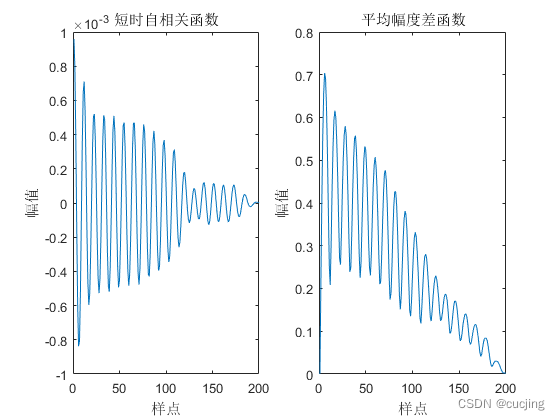
图3.1 韵母a的短时自相关函数和短时平均幅度差函数
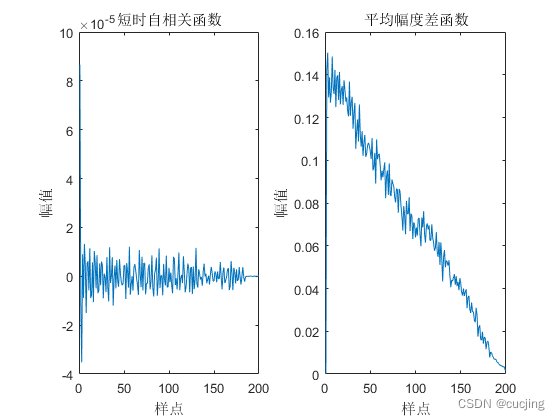
图3.2 清音s的短时自相关函数和短时平均幅度差函数
由上图看出,浊音a和清音s的短时自相关函数和短时平均幅度差函数特点:
1.短时自相关函数和短时平均幅度差函数可明显反映出浊音信号周期性。在周期的整数倍上,自相关函数可以达到最大值,其中R(0)最大。
2.清音短时自相关函数和平均幅度差函数没有周期性,也不具明显突出峰值,性质类似于噪声。
(二)韵母a的改进的短时自相关函数和改进的短时平均幅度差函数
%读取语音信号
[y,fs] = audioread('a.wav');%读出信号
y1=filter([1 -0.98],1,y);%预加重
N=length(y1);
time=(0:N-1)/fs;
%加窗分帧处理
wlen=200; % 帧长
inc=100; % 帧移
win=boxcar(wlen);
y2=enframe(y1,win,inc)'; % 分帧后的数组(帧长×帧数)
x=y2(:,i); %获取某一帧的数据
%短时自相关函数
for k=1:wlen
R(k)=sum(x(k:end).*x(1:end-k+1));
end
%短时平均幅度差函数
for m=1:wlen
amdfvec(m) = sum(abs(x(m:end)-x(1:end-m+1))); % 求每个样点的幅度差再累加
end
%修正短时自相关函数和修正短时平均幅度差函数
M1=100;
M2=100;
R1=zeros(1,fn);
amdfvec1=zeros(1,fn);
for a=1:M1
for b=1:M2
R1(a)=R1(a)+x(b)*x(b+a-1);
amdfvec1(a)= amdfvec1(a)+abs(x(b)-x(b+a-1));
end
end
% 画图
subplot(2,2,1); %短时自相关函数
plot(R);
title('短时自相关函数');
ylabel('幅值');
xlabel('样点' );
subplot(2,2,2); %修正短时自相关函数
plot(R1);
title('修正短时自相关函数');
ylabel('幅值');
xlabel('样点' );
subplot(2,2,3); %平均幅度差函数
plot(amdfvec);
title('平均幅度差函数');
ylabel('幅值');
xlabel('样点' );
subplot(2,2,4); %修正短时平均幅度差函数
plot(amdfvec1);
title('修正平均幅度差函数');
ylabel('幅值');
xlabel('样点' );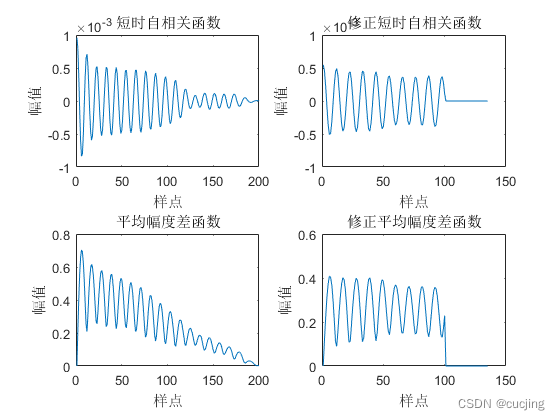
图3.3 韵母a的改进的短时自相关函数和改进的短时平均幅度差函数
由图可知,与短时自相关函数和短时平均幅度差函数相比,采用改进的自相关函数和平均幅度差函数后,在周期倍数上仍然有峰值,且幅值没有明显下降,窗长的变小,不会影响到基音周期附近最大值的出现。
(三)用改进后的短时自相关法和短时平均幅度差估计韵母o的基频数值并将其基频曲线画出来,加入三电平削波和中值平滑;与praat求得的结果相比较(两者的帧长帧移等数值要设置成一样的)
%读取语音信号
[y,fs] = audioread('o.wav');%读出信号
y=y/max(abs(y));% 幅度归一化
N=length(y);
time=(0:N-1)/fs;
%语音信号对称
m1=max(y);%找到归一化后数据最大值
m2=min(y); %找到最小值
m0=(m1+m2)/2; %为保证幅度值与横坐标轴对称
for i=1:N
y(i)=y(i)-m0;
end
%三电平削波
Amax=0.7*max(y);
for k=1:N
if(y(k)<-Amax)
y(k)=-1;
elseif(y(k)>Amax)
y(k)=1;
elseif(y(k)>=-Amax && y(k)<=Amax)
y(k)=0;
end
end
%加窗分帧处理
wlen=350; % 帧长
inc=90; % 帧移
win=boxcar(wlen);
y1=enframe(y,win,inc)'; % 分帧后的数组(帧长×帧数)
fn=size(y1,2); % 获取帧数
%frameTime=((0:fn-1)*inc+wlen/2)*Ts;
%修正短时自相关函数
M1=100;
M2=150;
R=zeros(wlen,fn);
for i=1:fn
x=y1(:,i); %获取某一帧的数据
for a=1:M1
for b=1:M2
R(a,i)=R(a,i)+x(b)*x(b+a-1);
end
end
end
%提取基频
nmax=round(fs/50);
nmin=round(fs/500);
for m=1:fn
if(R(1,m)==0)
value(m)=0;
else
[Rmax(m) pos(m)]=max(R(nmin:nmax,m));
pos(m)=pos(m)+nmin-1;
value(m)=1/(pos(m)*Ts);
end
end
%中值平滑
pitch=medfilt1(value,5);
plot(pitch,'.');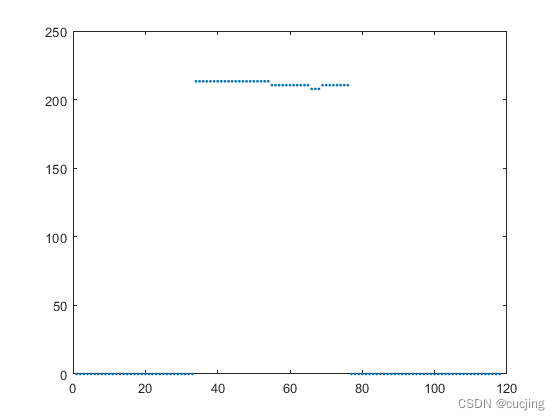
图3.4 MATLAB估计的韵母o的基频
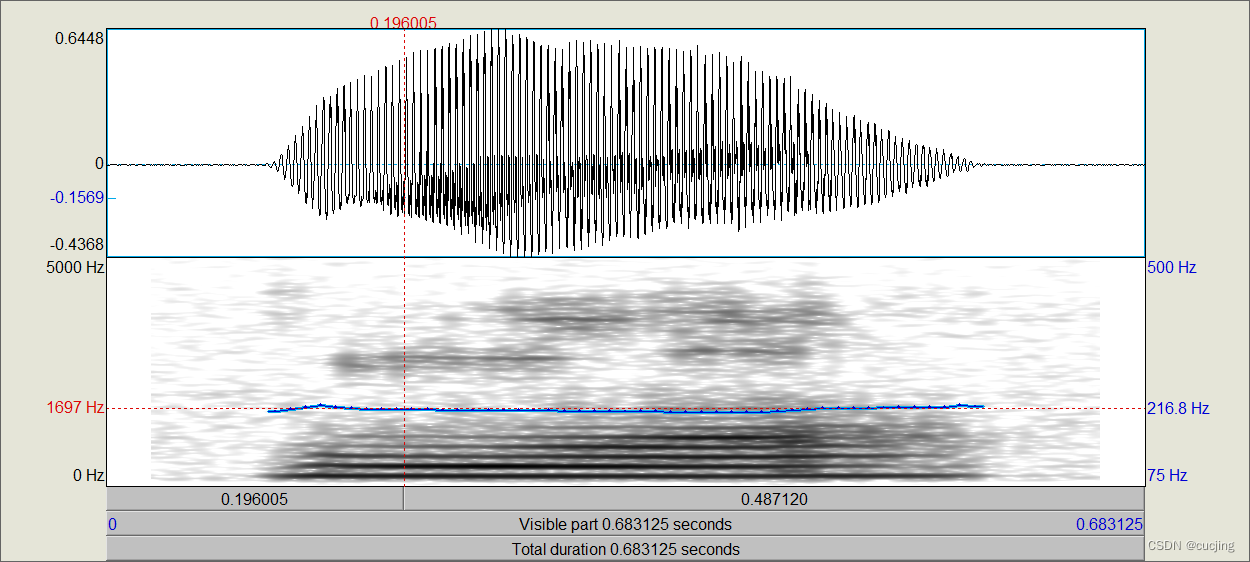
图3.5 Praat估计的韵母o的基频
由图可知,通过matlab估计韵母o基频值与通过praat测得o基频值(216.8Hz),相差不大。matlab中基频值是通过先三电平削波,再分帧求自相关得到的,求出来的基频曲线要比praat中的基频曲线时长短。
最后
以上就是害羞口红最近收集整理的关于语音的时频分析(二)的全部内容,更多相关语音内容请搜索靠谱客的其他文章。








发表评论 取消回复