自相关法中求解预测系数方程组为
方程的矩阵形式表示为:
式中R是正定对称的拓普利兹矩阵,且第个元素为
,a和r分别是元素为
和
的列向量。
上式中方程组可做如下变换:
写成矩阵形式为
根据最小均方误差公式,对于一个p阶最佳预测器,其最小均方预测误差为
写成矩阵的形式为
把上面两个矩阵合在一起,写成新p+1个方程,方程组满足p各未知预测器系数和对应的未知均方预测误差,新的矩阵方程为
上式中构造出的阶矩阵也是拓普利兹矩阵。该方程组用Levinson-Durbin算法递归求解。该算法通过在每次迭代中顺序地结合一个新的相关值来实现,并且根据新的相关值和已获得的预测器就能解出下一个高一阶的预测器。
对于任意阶数i,上式中的方程组都可以以矩阵形式表示:
我们希望第i阶的解是如何由第i-1阶的解导出的。换而言之是给定,即
的解,我们希望导出
的解。
1、先将矩阵方程以扩展形式写为
2、将数0附加到向量中,并与矩阵
相乘,这时得到新的一组i+1个方程:
上式成立的条件是:
3、根据拓普利兹矩阵的对称性,方程组可以以相反顺序写出(第一个方程写在最后面,最后一个方程写在最前面,以此类推),可得
4、将2和3两步中的公式合并可得
该式逼近了表达式,然后选择
使方程右边的向量只有一个非零元素,此时新参数
必须为
这样就确保方程右边的向量的最后一个元素为0,则此时第一个元素为
5、选定后,第i阶的预测系数向量为
6、可得系数更新方程组为
因此,对于某个特定的阶数p,最佳预测系数为
以上就是Levinson-Durbin算法的核心步骤,其算法的伪代码如下
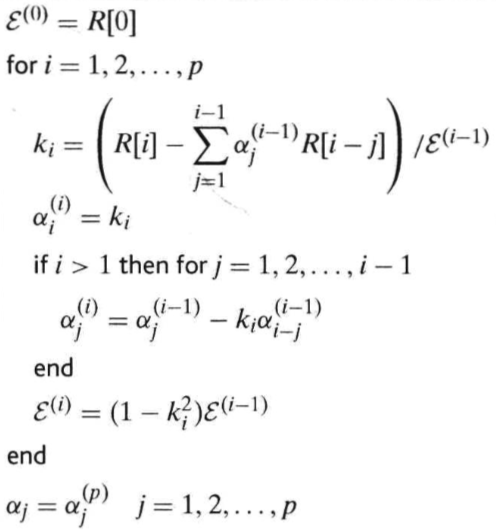
更多文章请关注公众号<<音频核>>

最后
以上就是缓慢皮皮虾最近收集整理的关于线性预测之Levinson-Durbin算法的全部内容,更多相关线性预测之Levinson-Durbin算法内容请搜索靠谱客的其他文章。








发表评论 取消回复