matlab求两向量夹角_MATLAB概率和统计(2)

7．max和min函数

函数max和min用于求向量或者矩阵的最大或最小元素，它们的调用格式基本相同，这里以max为例进行说明。

(1)C=max(A)：输入参数A可以是向量或矩阵，若为向量，则返回该向量中所有元素的最大值；若为矩阵，则返回一个行向量，向量中各个元素分别为矩阵各列元素的最大值。

(2)C=max(A,B)：比较A、B中对应元素的大小，A、B可以是矩阵或向量，要求尺寸相同，返回一个A、B中比较大元素组成的矩阵或向量。另外A、B中也可以有一个为标量，返回与该标量比较后得到的矩阵或向量。

(3)C=max(A,[],dim)：返回A中第dim维的最大值。

(4)[C,I]=max(…)：返回向量或矩阵中的最大值及其下标值。

【例4-22】  函数max和min使用示例。

>> A=magic(4)

A =

    16     2     3    13

     5    11    10     8

     9     7     6    12

     4    14    15     1

>> max(A)                    %  求最大值

ans =

    16    14    15    13

>> min(A)                    %  求最小值

ans =

     4     2     3     1

>> B=reshape(1:16,4,4)

B =

     1     5     9    13

     2     6    10    14

     3     7    11    15

     4     8    12    16

>> max(A,B)                  %  两个矩阵比较

ans =

    16     5     9    13

     5    11    10    14

     9     7    11    15

     4    14    15    16

>> [C,I]=min(A,[],2)       %  求行最小值并返回下标

C =

     2

     5

     6

     1

I =

     2

     1

     3

     4

8．mean函数

mean函数用于求向量或矩阵的平均值，其调用语法如下。

(1)M=mean(A)：若输入参数A为向量，就返回该向量所有元素的平均值；若为矩阵，则返回每列元素的平均值。

(2)M=mean(A,dim)：返回矩阵A第dim维方向各元素的平均值。

【例4-23】  mean函数使用示例。

>> A = reshape(1:25,5,5)

A =

     1     6    11    16    21

     2     7    12    17    22

     3     8    13    18    23

     4     9    14    19    24

     5    10    15    20    25

>> mean(A)       %  列方向求平均数

ans =

     3     8    13    18    23>> mean(A,2)    %  行方向求平均数

ans =

    11

    12

    13

    14

    15

9．median函数

median函数用于求向量或矩阵的中值，它是统计工具箱中的函数，其调用语法与mean函数类似，下面通过示例简要说明。

【例4-24】  median函数使用示例。

>> A = [1 2 4 4; 3 4 6 6; 5 6 8 8; 5 6 8 8]

A =

     1     2     4     4

     3     4     6     6

     5     6     8     8

     5     6     8     8

>> median(A)                %  列方向中值

ans =

     4     5     7     7

>> median(A,2)              %  行方向中值

ans =

     3

     5

     7

     7

10．std函数

std函数用于求向量或矩阵中元素的标准差。在一般的书中，标准差(standard deviation)有以下两种不同的计算方法(标准差与样本标准差)：

 其中：

n是样本的元素个数。这两种方法的区别在于：前面的除数一个是n-1，而另一个是n。

std函数调用语法如下。

(1)s=std(x)：若x为向量，按照公式(1)计算该向量元素的样本标准差；若x为矩阵，就返回x各列元素的标准差。

(2)s=std(x,flag)：若flag=0，则等同于s=std(x)；若flag=1，则按照公式(2)求x的标准差。

(3)s=std(x,flag,dim)：返回第dim维方向各元素的标准差。

【例4-25】  std函数使用示例。

>> A=magic(5)

A =

    17    24     1     8    15

    23     5     7    14    16

     4     6    13    20    22

    10    12    19    21     3

    11    18    25     2     9

>> s1=std(A,0,1)

s1 =

    7.2457    8.0623    9.4868    8.0623    7.2457

>> s2=std(A,1,1)

s2 =

    6.4807    7.2111    8.4853    7.2111    6.4807

>> s3=std(A,0,2)

s3 =

    8.8034

    7.2457

    8.0623

    7.2457

    8.8034

11．var函数

var函数用于求向量或矩阵中元素的方差。方差就是标准差的平方。var函数的调用语法如下。

(1)V = var(X)：若X为向量，则计算X的样本方差；若X为矩阵，则按列计算X的方差。

(2)V = var(X,1)：按照上面公式(2)中s的平方计算X的方差。

(3)V = var(X,w)：使用权重向量w计算方差。

(4)V = var(X,w,dim)：计算矩阵X第dim维的方差。

【例4-26】  var函数使用示例。

>> A=magic(5)

A =

    17    24     1     8    15

    23     5     7    14    16

     4     6    13    20    22

    10    12    19    21     3

    11    18    25     2     9

>> v1=var(A)                      %  样本方差

v1 =

   52.5000   65.0000   90.0000   65.0000   52.5000

>> v2=var(A,0,1)                  %  和v1结果相同

v2 =

   52.5000   65.0000   90.0000   65.0000   52.5000

>> v3=var(A,1,1)                  %  计算方差

v3 =

    42    52    72    52    42

12．cov函数

cov函数用于求协方差矩阵，计算协方差的数学公式为：cov(x₁,x₂)=E[(x₁-u₁)(x₂-u₂)]。其中，E是数学期望，u₁=Ex₁,u₂=Ex₂。cov函数的调用语法如下。

(1)C=cov(x)：若x为一向量，返回的则是向量元素的方差，为一标量；若x为一个矩阵，则返回协方差矩阵。

(2)C=cov(x,y)：计算列向量x、y的协方差，要求x、y具有相等的元素个数。如果x、y是矩阵，那么MATLAB会将其转换为列向量，相当于cov([A(:),B(:)])。

【例4-27】  cov函数使用示例。

>> A = [-1 1 2 ; -2 3 1 ; 4 0 3]

A =

    -1     1     2

    -2     3     1

     4     0     3

>> C=cov(A)                       %  协方差矩阵

C =

   10.3333   -4.1667    3.0000

   -4.1667    2.3333   -1.5000

    3.0000   -1.5000    1.0000

>> v = diag(cov(A))'              %  矩阵A每列的方差

v =

   10.3333    2.3333    1.0000

>> V = var(A)                  %  矩阵A每列的方差

V =

   10.3333    2.3333    1.0000

通过比较可以看出，协方差矩阵主对角线上的元素就是每列的方差。

13．corrcoef函数

corrcoef函数用来计算矩阵相关系数。相关系数用符号表示，是一个无量纲量，计算公式为：。函数corrcoef的调用语法如下。

(1)corrcoef(x)：若x为一个矩阵，返回的则是一个相关系数矩阵，其尺寸与矩阵x一样。

(2)corrcoef(x,y)：计算列向量x、y的相关系数，要求x、y具有相等的元素个数。如果x、y是矩阵，那么corrcoef函数会将其转换为列向量，相当于corrcoef([x(:),y(:)])。

【例4-28】  随机生成一组数据，考察第4列和其他列的相关性。

>> x = randn(30,4);     %  无关联的数据

>> x(:,4) = sum(x,2);    %  引入相关性

>> [r,p] = corrcoef(x)  %   计算样本相关性和p值

r =

    1.0000    0.3006   -0.1030    0.6403

    0.3006    1.0000   -0.1786    0.6412

   -0.1030   -0.1786    1.0000    0.2719

    0.6403    0.6412    0.2719    1.0000

p =

    1.0000    0.1065    0.5881    0.0001

    0.1065    1.0000    0.3449    0.0001

    0.5881    0.3449    1.0000    0.1461

    0.0001    0.0001    0.1461    1.0000

>> [i,j] = find(p<0.05);  %  查找显著性相关

>> [i,j]                    %  显示下标索引

ans =

     4     1

     4     2

     1     4

     2     4

4.3.2  概率函数、分布函数、逆分布函数和随机数

以往要知道一个事件发生的概率、置信区间，几乎离不开查表。至于绘制概率密度函数、分布函数、图示置信区间，则需要付出更多的劳动。现在，借助MATLAB不但可以简洁而高效地解决以上问题，而且可以更加自如地进行复杂问题的研究工作。

表4-1中列出了7种常见分布的4组命令。这4组命令是：概率密度函数、累积分布函数、逆累积分布函数、随机数发生器。

表4-1 7种常见分布的相关函数

分布名称	概率密度函数	累积分布函数	逆累积分布函数	随机数发生器
二项分布	binopdf	binocdf	binoinv	binornd
泊松分布	poisspdf	poisscdf	poissinv	poissrnd
正态分布	normpdf	normcdf	norminv	normrnd

续表

分布名称	概率密度函数	累积分布函数	逆累积分布函数	随机数发生器
均匀分布	unifpdf	unifcdf	unifinv	unifrnd
分布	chi2pdf	chi2cdf	chi2inv	chi2rnd
F分布	fpdf	fcdf	finv	frnd
t分布	tpdf	tcdf	tinv	trnd

由于篇幅有限，本小节只举例介绍泊松分布、正态分布和分布。其他分布相应函数的使用方法类似，不再赘述。

【例4-29】  泊松分布与正态分布的关系。

当泊松分布的>10时，该泊松分布十分接近正态分布。泊松分布的概率密度函数和相对应的正态分布概率密度函数的计算可以使用如下命令：

>> Lambda=20;x=0:50;yd_p=poisspdf(x,Lambda); %  泊松分布

>> yd_n=normpdf(x,Lambda,sqrt(Lambda));      %  正态分布

本例通过画图对两种分布进行比较，结果如图4-1所示。

>> plot(x,yd_n,'b-',x,yd_p,'r+')                 %  绘图

>> text(30,0.07,'fontsize{12} {mu} = {lambda} = 20')  %  在图中作标注

【例4-30】  分布逆累积分布函数应用示例。

>> v=4;xi=0.9;x_xi=chi2inv(xi,v);  %  设置信水平为90%

>> x=0:0.1:15;yd_c=chi2pdf(x,v);   %  计算 (4)的概率密度函数

%  绘制图形，并给置信区间填色

>> plot(x,yd_c,'b'),hold on

>> xxf=0:0.1:x_xi;yyf=chi2pdf(xxf,v);    %  为填色而计算

>> fill([xxf,x_xi],[yyf,0],'g')          %  加入点(x_xi,0)使填色区域封闭

%  添加注释

>> text(x_xi*1.01,0.01,num2str(x_xi))     

>> text(10,0.16,['fontsize{16} x~{chi}^2' '(4)'])

>> text(1.5,0.08,'fontname{隶书}fontsize{22}置信水平0.9')

>> hold off

得到的结果如图4-2所示。

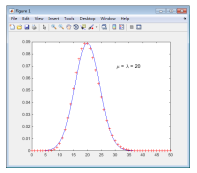
图4-1  =20的泊松分布和=20的正态分布的比较  

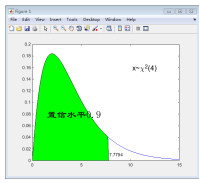
图4-2  分布水平为90%的置信区间