matlab泊松分布随机数和图像_浅谈可靠性理论中的常用概率分布

浅谈可靠性理论中的常用概率分布

1. 泊松分布

基本原理

泊松分布是最常见的离散概率分布，适合描述单位时间内随机事件发生的概率。

(1) 泊松分布概率密度(不可靠度)计算公式

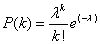
MATLAB概率密度函数poisspdf

调用格式：

Y=poisspdf(x,λ)，其中，x为随机变量；λ为不可靠度；

(2) 泊松分布累积概率密度函数(不可靠度函数)

MATLAB累积概率密度函数poisscdf

调用格式：

Y=poisscdf(x,λ)，

Y=poisscdf(x,λ,’upper’)，

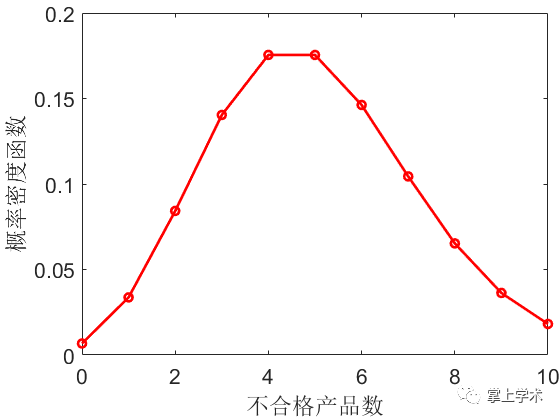
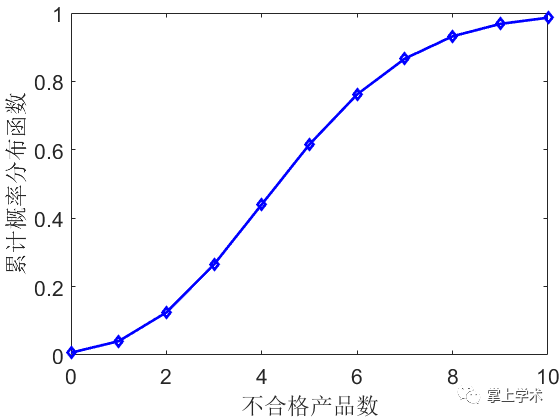
案例：一批产品的不合格率为5%，每100个产品装一瓶，求一瓶中含有0,1,…,10个不合格的概率及不合格产品在10个以下的概率。

MATLAB代码：

x=0:10;

s=100;

p=0.05

lamda=p*s;

ratio_pdf=poisspdf(x,lamda);%不合格概率

p_total=poisscdf(x,lamda);%10个以下不合格的概率

plot(x,ratio_pdf,'r-o','linewidth',2)

xlabel('不合格产品数')

ylabel('概率密度函数')

set(gca,'fontsize',16,'looseinset',[0 0 7 6])

figure

plot(x,p_total,'b-d','linewidth',2)

xlabel('不合格产品数')

ylabel('累计概率分布函数')

set(gca,'fontsize',16,'looseinset',[0 0 7 6])

分析结果

2. 正态分布

基本原理

由大量相互独立、微小的随机因素总和构成，且每个随机因素对总和的影响是均匀微小的。

(1) 正态分布概率密度(不可靠度)计算公式

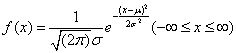
MATLAB概率密度函数normpdf

调用格式：

Y=normpdf(x,μ,σ)

Y=normpdf(x)

Y=normpdf(x,μ)

其中，x为随机变量；μ为均值；σ为标准差；

(2)  正态分布概率累积分布函数

MATLAB概率概率累积分布函数normcdf

调用格式：

p=normcdf(x)

p=normcdf(x, μ, σ)

[p,plo,pup]=normcdf(x, μ, σ,pcov,alpha)

其中，pcov为协方差矩阵；alpha为置信区间。

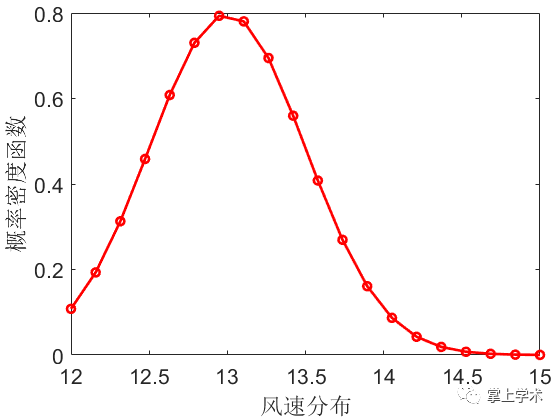
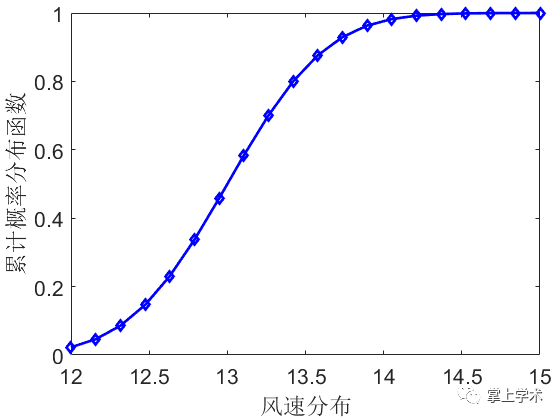
案例：已知某风场风速满足正态分布，其风速均值为13m/s，标准差为0.5。求风速在12~15m/s的概率分布和累计分布。

MATLAB代码：

x=linspace(12,15,20);

miu=13;

sigma=0.5;

ratio_pdf=normpdf(x,miu,sigma);%概率分布

p_total=normcdf(x,miu,sigma);%累计分布

plot(x,ratio_pdf,'r-o','linewidth',2)

xlabel('风速分布')

ylabel('概率密度函数')

set(gca,'fontsize',16,'looseinset',[0 0 7 6])

figure

plot(x,p_total,'b-d','linewidth',2)

xlabel('风速分布')

ylabel('累积概率分布函数')

set(gca,'fontsize',16,'looseinset',[0 0 7 6])

分析结果

3. 指数分布

基本原理

指数分布最显著的特征是失效率为常数，无记忆性，是无累计效应失效。

局限性

指数分布与机械零件的磨损、疲劳、腐蚀和蠕变等过程是完全矛盾的，与产品的损伤累积和老化相违背，不能作为机械零件功能参数的分布形式；对失效率变化的情况，指数分布无法有效模拟。

(1)指数分布概率密度(不可靠度)计算公式

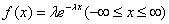
MATLAB概率密度函数exppdf

调用格式：

Y=exppdf(x, μ)

(2) 指数分布概率累积分布函数

MATLAB概率概率累积分布函数expcdf

调用格式：

p=expcdf(x,mu)

[p,plo,pup]=expcdf(x,mu,pcov,alpha)

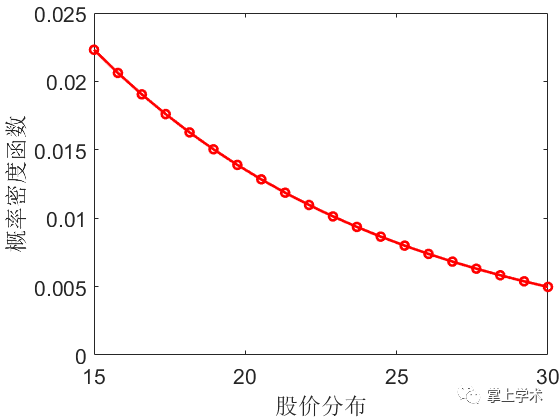
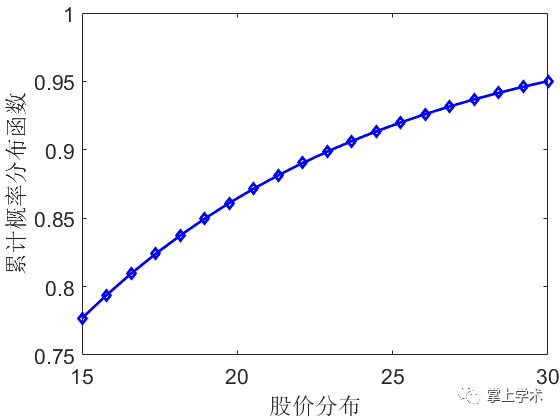
案例：某股市成指数增长，其价格均值为20，求股价在15~30之间的概率分布及累积分布。

MATLAB代码：

x=linspace(15,30,20);

miu=10;

ratio_pdf=exppdf(x,miu);%概率分布

p_total=expcdf(x,miu);;%累计分布

plot(x,ratio_pdf,'r-o','linewidth',2)

xlabel('股价分布')

ylabel('概率密度函数')

set(gca,'fontsize',16,'looseinset',[0 0 7 6])

figure

plot(x,p_total,'b-d','linewidth',2)

xlabel('股价分布')

ylabel('累积概率分布函数')

set(gca,'fontsize',16,'looseinset',[0 0 7 6])

分析结果

4. 对数正态分布

基本原理

随机变量由诸多影响因素构成，但这些因素对变量的影响并非均匀微小，而是其中一些因素对变量具有显著影响时，变量将趋于偏斜进而形成对数正态分布

(1) 对数正态分布概率密度(不可靠度)计算公式

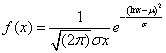
MATLAB概率密度函数lognpdf

调用格式：

Y=lognpdf(x,mu,sigma)

(2)对数正态分布概率累积分布函数

MATLAB概率概率累积分布函数logncdf

调用格式：

p=logncdf(x,mu,sigma)

[p,plo,pup]=logncdf(x,mu,sigma,pcov,alpha)

其中，plo为置信区间下边界；pup为置信区间上边界；

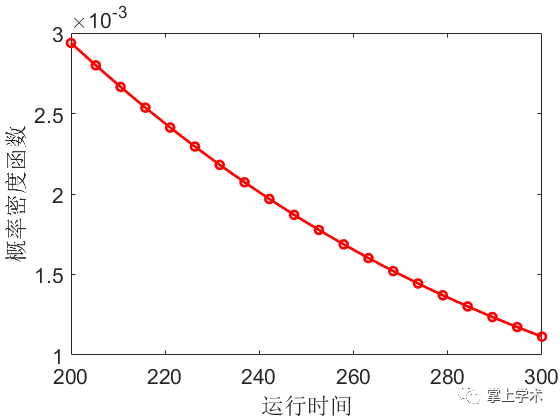
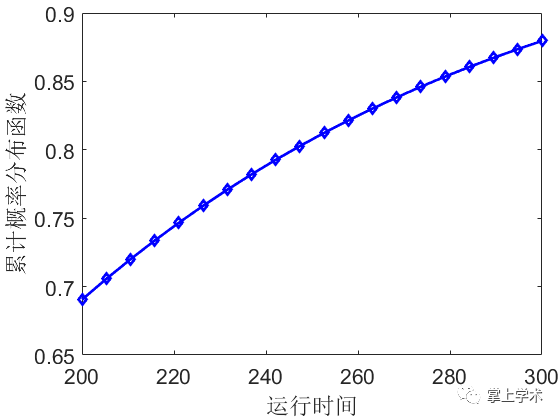
案例：某风机叶片的疲劳寿命服从对数正态分布，且均值为5，标准差为0.6，求该风机叶片在运行200~300天内的疲劳概率与累积概率分布

MATLAB代码：

x=linspace(200,300,20);

mu=5;

sigma=0.6;

ratio_pdf=lognpdf(x,mu,sigma);

p_total=logncdf(x,mu,sigma);

plot(x,ratio_pdf,'r-o','linewidth',2)

xlabel('运行时间')

ylabel('概率密度函数')

set(gca,'fontsize',16,'looseinset',[0 0 7 6])

figure

plot(x,p_total,'b-d','linewidth',2)

xlabel('运行时间')

ylabel('累积概率分布函数')

set(gca,'fontsize',16,'looseinset',[0 0 7 6])

分析结果

5. 伽马分布

基本原理

伽马分布是统计学的一种连续概率分布，是n个随机事件均发生需要经历的时间。

(1)伽马分布概率密度(不可靠度)计算公式

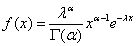
MATLAB概率密度函数gampdf

调用格式：

Y=gampdf(x,A,B)

其中，x为随机变量；A为形状参数；B为尺度参数；

(2)伽马分布概率累积分布函数

MATLAB概率概率累积分布函数gamcdf

调用格式：

Y=gamcdf(x,A,B)

[p,plo,pup]=gamcdf(x,A,B,pcov,alpha)

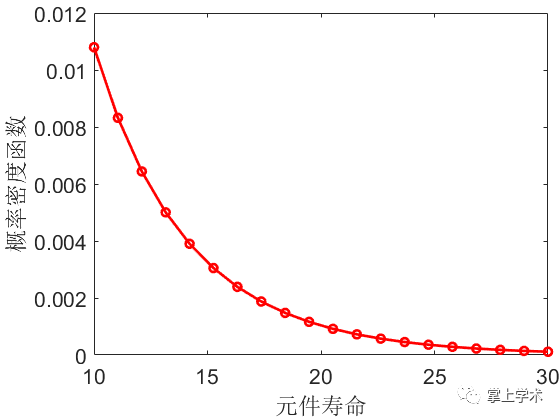
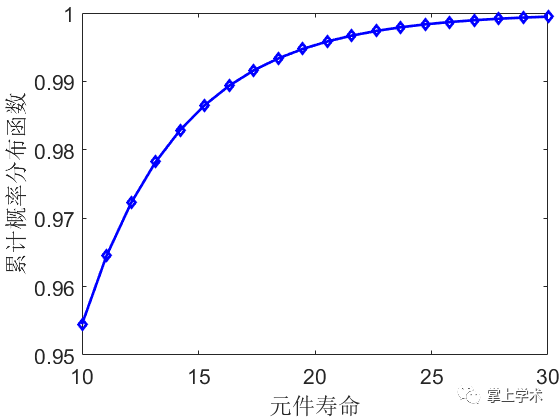
案例：某元件寿命服从伽马分布，其形状参数为0.5，尺度参数为5，求其元件寿命在10~30天的概率分布和累计分布情况

MATLAB代码：

x=linspace(10,30,20);

a=0.5;

b=5;

ratio_pdf=gampdf(x,a,b);%概率分布

p_total=gamcdf(x,a,b);%累计分布

plot(x,ratio_pdf,'r-o','linewidth',2)

xlabel('元件寿命')

ylabel('概率密度函数')

set(gca,'fontsize',16,'looseinset',[0 0 7 6])

figure

plot(x,p_total,'b-d','linewidth',2)

xlabel('元件寿命')

ylabel('累积概率分布函数')

set(gca,'fontsize',16,'looseinset',[0 0 7 6])

分析结果

6.三参数威布尔分布

基本原理

威布尔分布模型是研究机械零部件可靠性最适合的模型之一，是由某一局部失效导致全局停止运行的最弱环节模型。

(1)三参数威布尔分布概率密度(不可靠度)计算公式

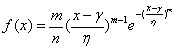
MATLAB三参数威布尔概率密度函数wblpdf

调用格式：

Y=wblpdf(x,A,B)

其中，x为随即变量；A为尺度参数；B为形状参数。

(2)  三参数威布尔分布概率累积分布函数

MATLAB三参数威布尔概率累积分布函数wblcdf

调用格式：

p=wblcdf(x,a,b)

[p,plo,pup]=wblcdf(x,A,B,pcov,alpha)

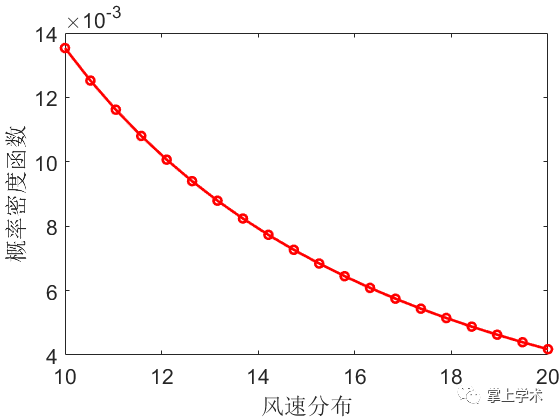
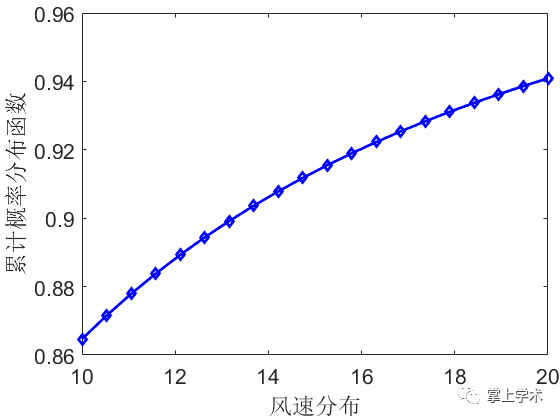
案例：已知风速在10~20之间的形状参数为0.8，尺度参数为3，求风速的概率密度分布和累计分布。

MATLAB代码：

x=linspace(10,20,20);

b=0.5;

a=2.5;

ratio_pdf=wblpdf(x,a,b);%概率分布

p_total=wblcdf(x,a,b);;%累计分布

plot(x,ratio_pdf,'r-o','linewidth',2)

xlabel('风速分布')

ylabel('概率密度函数')

set(gca,'fontsize',16,'looseinset',[0 0 7 6])

figure

plot(x,p_total,'b-d','linewidth',2)

xlabel('风速分布')

ylabel('累积概率分布函数')

set(gca,'fontsize',16,'looseinset',[0 0 7 6])

分析结果

把时间交给阅读