一、统计概率
1.1 随机变量(通常用大写字母表示)
量化随机事件的函数,将随机事件可能出现的结果赋予了一个数字。

1.2 概率分布
- 概率分布=随机变量+概率+分布(在统计图中的形状);
- Python实现:科学计算SciPy的stats模块;
#anaconda prompt下安装scipy包
conda install scipy
#导入包,统计计算包的统计模块
import scipy.stats as stats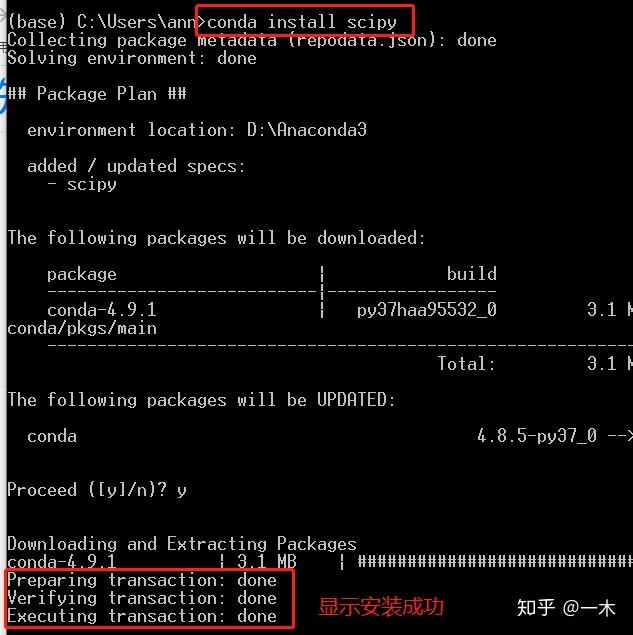
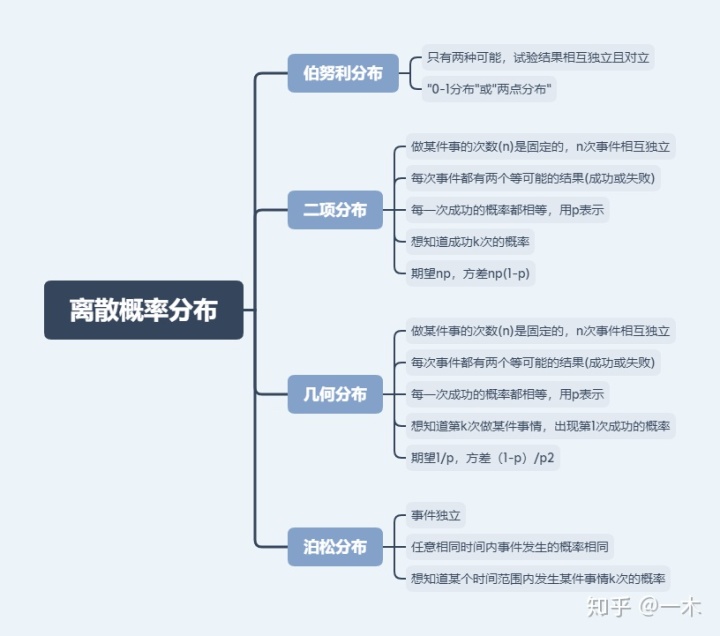
1.3 离散概率分布
附加知识点:因为Python绘图时坐标轴不显示中文,需要进行修改,网上有好几种修改方法,我自己改过两次配置文件,一次改坏了,一次改了没反应,所以不推荐这种方式,尝试了动态设置参数,稍微麻烦些,每次使用都要设置,但是可以应急,把设置代码放在下面,亲测有用,还有其他没尝试过的方法,待以后解决。
#设置显示中文字体
from pylab import mpl
mpl.rcParams['font.sans-serif'] = ['FangSong'] # 指定默认字体
mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题伯努利分布Python实现:
#导入包
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
#第一步,定义随机变量1和0,抛硬币正面朝上为1,反面朝上为0
X=np.arange(0,2,1) #生成等差数组,arrange(start,stop,step)
#第二步:求对应分布的概率质量函数(PMF),返回一个列表,列表中每个元素表示随机变量中对应值的概率
p=0.5 #硬币朝上概率
plist=stats.bernoulli.pmf(X,p)
'''
plot默认绘制折线,因为是离散随机变量,只绘制点,所以传入以下参数:marker:点的形状, o表示为圆圈标记;
linestyle:线条的形状,值None表示不显示连接各个点的折线; vlines用于绘制竖直线,vline(X坐标值,
y最小坐标值,y最大坐标值);传入的X是一个数组, 是给数组中的每个X坐标值绘制竖直线,y最小坐标值是0,
最大坐标值是对用plist中的值。
'''
#第3步:绘图
plt.plot(X,plist,marker='o',linestyle='None')
plt.vlines(X,0,plist)
#设置显示中文字体
from pylab import mpl
mpl.rcParams['font.sans-serif'] = ['FangSong'] # 指定默认字体
mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题
#x轴文本
plt.xlabel('随机变量:抛硬币1次')
#y轴文本
plt.ylabel('概率')
#标题
plt.title('伯努利分布:p=%.2f' % p)
#显示图形
plt.show()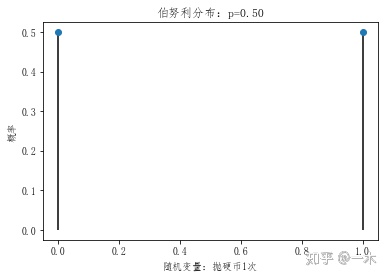
二项分布Python实现:
#导入包
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
#第一步,定义随机变量:抛硬币5次,正面朝上的概率
n=5 #次数
p=0.5 #成功的概率
X=np.arange(0,n+1,1) #生成等差数组,arrange(start,stop,step)
#第二步:求对应分布的概率质量函数(PMF),返回一个列表,列表中每个元素表示随机变量中对应值的概率
plist=stats.binom.pmf(X,n,p)
#第3步:绘图
plt.plot(X,plist,marker='o',linestyle='None')
plt.vlines(X,0,plist)
#设置显示中文字体
from pylab import mpl
mpl.rcParams['font.sans-serif'] = ['FangSong'] # 指定默认字体
mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题
#x轴文本
plt.xlabel('随机变量:抛硬币正面朝上次数')
#y轴文本
plt.ylabel('概率')
#标题
plt.title('二项分布:n=%i,p=%.2f' % (n,p))
#显示图形
plt.show()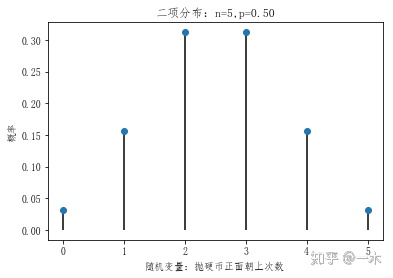
几何分布Python实现:
#导入包
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
#第一步,定义随机变量:首次成功的次数,可能是1次,2次,3次等,这里我们想知道5次成功的概率
n=6 #次数
p=0.7 #成功的概率
X=np.arange(1,n+1,1) #生成等差数组,arrange(start,stop,step)
#第二步:求对应分布的概率质量函数(PMF),返回一个列表,列表中每个元素表示随机变量中对应值的概率
plist=stats.geom.pmf(X,p)
#第3步:绘图
plt.plot(X,plist,marker='o',linestyle='None')
plt.vlines(X,0,plist)
#设置显示中文字体
from pylab import mpl
mpl.rcParams['font.sans-serif'] = ['FangSong'] # 指定默认字体
mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题
#x轴文本
plt.xlabel('随机变量:第n次首次成功')
#y轴文本
plt.ylabel('概率')
#标题
plt.title('几何分布:p=%.2f' % p)
#显示图形
plt.show()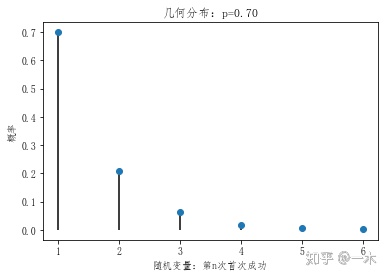
泊松分布Python实现:
#导入包
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
#第一步,定义随机变量:已知班主任透过窗户盯人的概率是每天2次,那么一天内盯人k次的概率是?
mean=2 #均值,每天盯2次
k=5 #每天盯5次的概率
X=np.arange(0,k+1,1) #生成等差数组,arrange(start,stop,step)
#第二步:求对应分布的概率质量函数(PMF),返回一个列表,列表中每个元素表示随机变量中对应值的概率
plist=stats.poisson.pmf(X,mean)
#第3步:绘图
plt.plot(X,plist,marker='o',linestyle='None')
plt.vlines(X,0,plist)
#设置显示中文字体
from pylab import mpl
mpl.rcParams['font.sans-serif'] = ['FangSong'] # 指定默认字体
mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题
#x轴文本
plt.xlabel('随机变量:盯人k次')
#y轴文本
plt.ylabel('概率')
#标题
plt.title('泊松分布:均值mean=%i' % mean)
#显示图形
plt.show()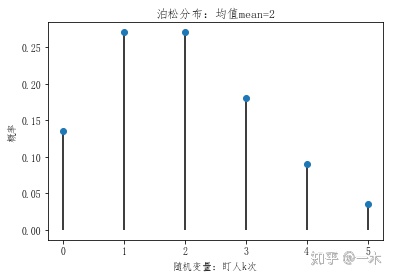
1.4 连续概率分布
- 正态分布[1];
- 幂律分布[2];
正态分布Python实现:
#导入包
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
#第一步,定义随机变量
mu=0 #均值
sigma=1 #标准差
X=np.arange(-5,5,0.1) #生成等差数组,arrange(start,stop,step)
#第二步:求对应分布的概率密度函数(PDF)
y=stats.norm.pdf(X,mu,sigma)
#第3步:绘图
plt.plot(X,y)
#设置显示中文字体
from pylab import mpl
mpl.rcParams['font.sans-serif'] = ['FangSong'] # 指定默认字体
mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题
#x轴文本
plt.xlabel('随机变量:X')
#y轴文本
plt.ylabel('概率:y')
#标题
plt.title('正态分布:$mu$=%.1f,$sigma^2$=%.1f' %(mu,sigma))
#网格
plt.grid()
#显示图形
plt.show()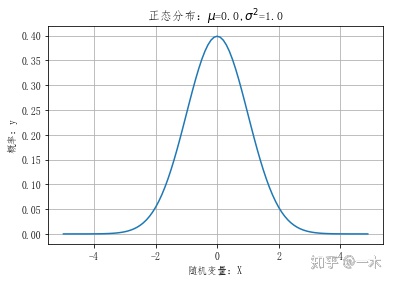
二、统计概率
2.1 总体和样本
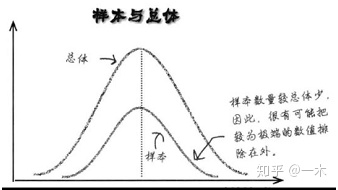
总体是研究对象的全部,样本是从总体中抽出的部分单位集合,这个集合的大小叫做样本量,样本个数指从总体中可能抽取的样本数[3],比如一个代销为500的样本,从中抽取100个调查,则样本个数为100。

相关Python模块是随机数(random)包,randint()函数可生成随机数。
#生成随机数x,x为a到b之间的数字(a<= x <=b)
import random
x = random.randint(a,b)
#案例,生成[0,9]之间的随机数a
a = random.randint(0,9)用Python实现一个小抽奖:
#导入random(随机数)模块
import random
'''
range()函数创建一个整数列表,一般用在for循环中。
range(start,stop,step),计数从start开始,默认为0,不包括stop,
步长step默认为1.如range(0,5)等价于range(0,5,1)
'''
#抽奖,从1000个用户中随机抽取5个人作为中奖者
for i in range(1,6):
userid=random.randint(1,1000)
#用%s格式化字符串
print('第 %s 位获奖用户id是 %s' % (i,userid))
pandas数据框DataFrame抽样方法:
import numpy as np #数组包
import pandas as pd #数据分析包
'''
arange()函数产生一个含有5*4个元素的一维数组;
reshape:将数组转换为5行4列的二维数组
'''
df = pd.DataFrame(np.arange(5*4).reshape(5,4))
#随机选择一个n行的子集
sample1 = df.sample(n=3)
sample1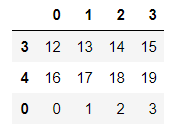
2.2 中心极限定理
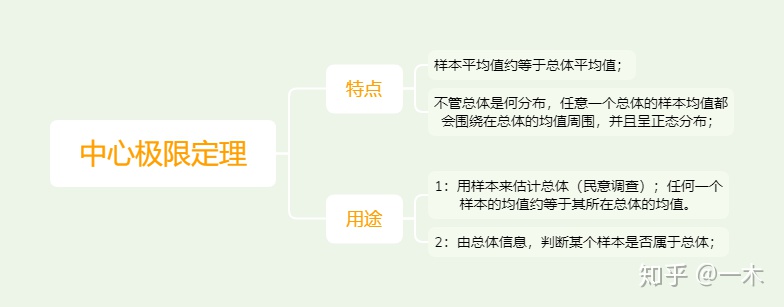
2.3 样本估计总体标准差
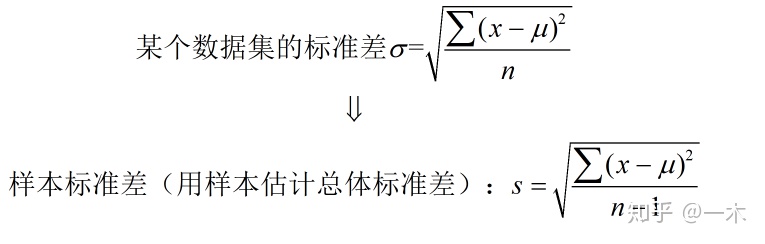
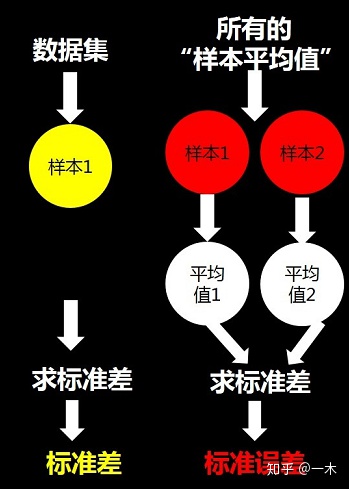
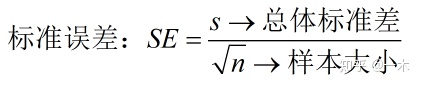
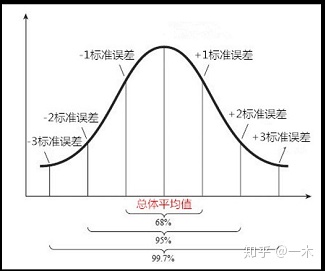
2.4 概率“偏见”

参考
- ^正态分布百科 https://baike.baidu.com/item/%E6%AD%A3%E6%80%81%E5%88%86%E5%B8%83
- ^幂律分布百科 https://baike.baidu.com/item/%E5%B9%82%E5%BE%8B%E5%88%86%E5%B8%83
- ^样本容量MBA智库百科 https://wiki.mbalib.com/wiki/%E6%A0%B7%E6%9C%AC%E5%AE%B9%E9%87%8F
最后
以上就是落寞曲奇最近收集整理的关于matlab泊松分布随机数和图像_统计概率思维及几种分布的Python实现的全部内容,更多相关matlab泊松分布随机数和图像_统计概率思维及几种分布内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复