3 概率分布与随机函数

53 阅读 0 评论 35 点赞

我是靠谱客的博主安静指甲油，最近开发中收集的这篇文章主要介绍3 概率分布与随机函数，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

更多MATLAB数据分析视频请点击，或者在网易云课堂上搜索《MATLAB数据分析与统计》 http://study.163.com/course/courseMain.htm?courseId=1003615016

随着计算机技术的快速发展，随机数在越来越多的领域得到了广泛应用，例如信息安全，网络游戏，计算机仿真和模拟计算，这一章将介绍常用的概率分布及概率计算、利用MATLAB生成随机数。

1.概率分布及概率计算

1.1 概率分布的定义

设X为一随机变量，对任意实数x，定义

F（x）=P（X<=x）

为X的分布函数。根据随机变量取值的特定，随机变量分为离散型和连续型两种。P为X的概率函数

1.2 几种常见的概率分布

（1）二项分布

若随机变量X的概率函数为

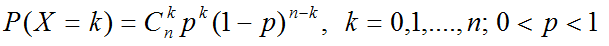
则称X服从二项分布，记为X~B（n，p）。其期望E（X）=np，方差var（X）=np（1-p）。

（2）泊松分布

若随机变量X的概率函数为

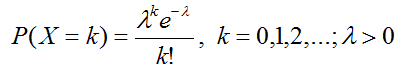
则称X服从参数为λ的泊松分布，记为X~P（λ）。其期望E（x）=λ，方差var（X）=λ。

（3）离散均匀分布

若随机变量X的概率函数为

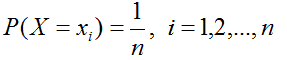
则称X服从离散的均匀分布

（4）连续均匀分布

若随机变量X的概率密度函数为

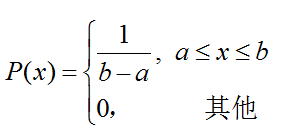
则称X服从区间[a,b]上的连续均匀分布，记为X~U（a，b）。其期望E（X）=（a+b）/2，方差var(X)=(b-a)^2/12.

（5）指数分布

若随机变量X的概率密度函数为

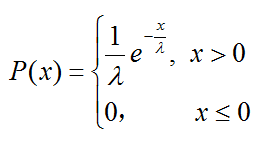
其中λ>0为参数，则称X服从指数分布，记为X~Exp（λ）。其期望E（X）=λ，方差var（x）=λ^2

（6）正态分布

若随机变量X的概率密度函数为

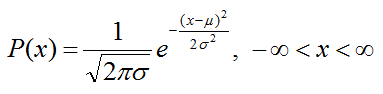
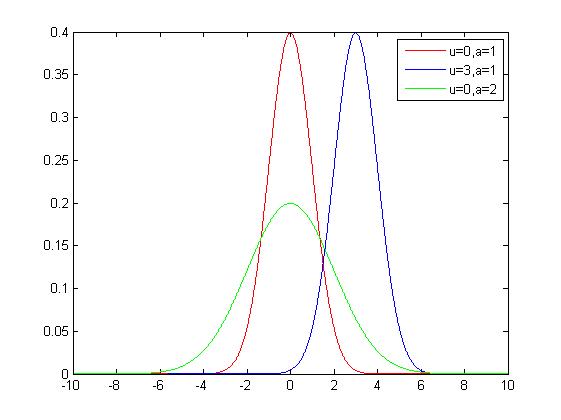
其中，σ>0,μ为分布参数，则称X服从正态分布，记为X~N（μ，σ^2）,其期望E（X）=μ，方差var（X）=σ^2。特别地，当μ=0，σ=1时，称X服从标准正态分布，记为X~N（0,1）。

（7）卡方分布

若n个相互独立的随机变量ξ₁、ξ₂、……、ξn ，均服从标准正态分布（也称独立同分布于标准正态分布），则这n个服从标准正态分布的随机变量的平方和

构成一新的随机变量，其

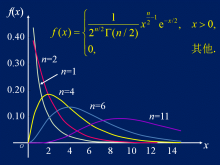卡方分布

分布规律称为

分布（chi-square distribution），其中参数n称为自由度，正如正态分布中均值或方差不同就是另一个正态分布一样，自由度不同就是另一个

分布。记为

或者

卡方分布是由正态分布构造而成的一个新的分布，当自由度n很大时，

分布近似为正态分布

（8）t分布

设随机变量X与Y相互独立，X服从N(0,1)分布，Y服从自由度为k的卡方分布，则称随机变量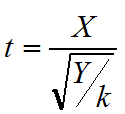所服从的分布是自由度为k的t分布，记做 t~t(k)

（9）F分布

设随机变量X和Y相互独立，分别服从自由度为k1,和k2的卡方分布，则称随机变量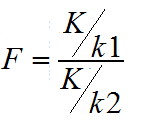所服从的分布是自由度为（k1,k2）的F分布，记作F~F(k1,k2)。其中，k1称为第一自由度，k2称为第二自由度。

1.3 概率密度、分布函数和逆概率分布函数值的计算

MATLAB统计工具箱中有这样一系列函数，函数名以pdf三个字符结尾的函数用来计算常见连续分布的密度函数值或离散分布的概率函数值，函数名以cdf三个字符串结尾的函数用来计算常见分布的分布函数值，函数名以inv三个字符串结尾的函数用来计算常见分布的逆概率分布函数值。

MATLAB中常见分布函数列表

离散分布

二项分布（bino）

负二项分布（nbin）

几何分布（geo）

超几何分布（hyge）

泊松分布（poiss）

离散均匀分布（unid）

多项分布（mn）

连续分布

正态分布（norm）

对数正态分布（logn）

多元正态分布（mvn）

连续均匀分布（unif）

指数分布（exp）

卡方分布（chi2）

非中心卡方分布（ncx2）

t分布（t）

非中心t分布（nct）

多元t分布（mvt）

F分布（F）

非中心F分布（ncf）

威尔分布（wbl）

瑞利分布（rayl）

极值分布（ev）

广义极值分布（gev）

.....

在列出的上面这些常见分布名英文缩写后面加上pdf，cdf ，inv 就可得到计算常见分布的概率密度，分布函数值和逆概率分布函数值。

例：求服从均值为1.2345，标准差为6的正态分布随机变量X在x=0,1,2，.....，10处的密度函数值与分布函数值，并求概率P（-2<X<=5）

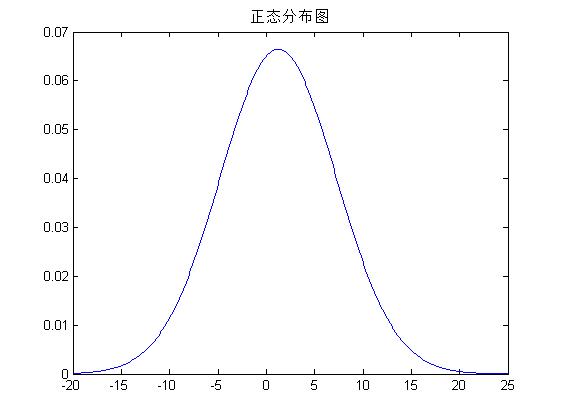
%--首先画出这个正态分布图
X=-20:0.1:25;
Y=normpdf(X,1.2345,6);
plot(X,Y);
title('正态分布图');

%定义一个x向量，然后求该向量对应处的概率密度值
x=0:10;
y=normpdf(x,1.2345,6)

%求x向量处所对应的分布函数值
F=normcdf(x,1.2345,6)

%求概率P（-2<X<=5）
P=normcdf(5,1.2345,6)-normcdf(-2,1.2345,6)

y =

    0.0651    0.0664    0.0660    0.0637    0.0598    0.0546    0.0485    0.0419    0.0352    0.0288    0.0229

F =

    0.4185    0.4844    0.5508    0.6157    0.6776    0.7349    0.7865    0.8317    0.8703    0.9022    0.9280

P =

    0.4399

2. 生成一元分布随机数

2.1 rand函数生成在 [0 ,1] 均匀分布随机数

调用格式：说明

Y=rand（n）生成nxn的随机数矩阵

Y=rand（m，n）生成mxn的随机矩阵

Y=rand（[m n]）生成mxn的随机矩阵

Y=rand（m，n，p，....）生成mxnxpx.....的随机矩阵或数组

Y=rand（[m n p ......]）生成mxnxpx.....的随机矩阵或数组

Y=rand（size（A））生成与矩阵或数组A具有相同大小的随机数矩阵或数组

其中，输入参数m，n，p.....应为正整数，如果输入负整数，则被认为是0，此时输出一个空矩阵

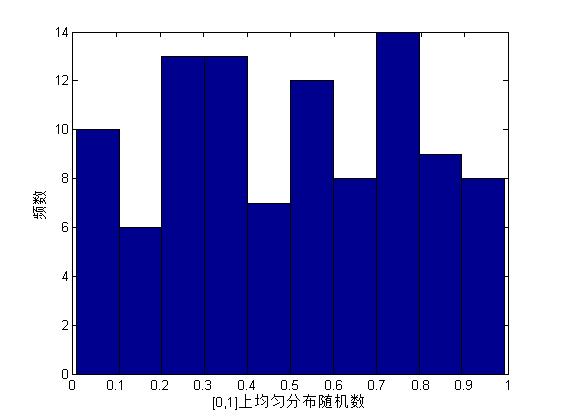
例：调用rand函数生成10x10的随机数矩阵，并将随机数矩阵按列拉长，然后调用hist函数画出频数直方图。

x=rand(10)     %生成10行10列的随机数矩阵，其元素在[0,1]上均匀分布

x =

    0.1427    0.8200    0.3579    0.7047    0.5575    0.5716    0.4143    0.6480    0.0531    0.7017
    0.4089    0.3180    0.6729    0.3311    0.4346    0.8517    0.9439    0.3242    0.8149    0.6110
    0.5818    0.3585    0.5933    0.5549    0.0934    0.6910    0.9925    0.4040    0.5675    0.3736
    0.1233    0.7055    0.2608    0.2878    0.2139    0.8443    0.2135    0.7093    0.5351    0.7440
    0.3646    0.7524    0.8828    0.3466    0.5959    0.2218    0.2759    0.9617    0.8090    0.0683
    0.7368    0.9677    0.9340    0.7834    0.0744    0.8586    0.5181    0.6870    0.6267    0.3361
    0.0374    0.0283    0.3005    0.2080    0.9345    0.3674    0.7654    0.8172    0.7334    0.0073
    0.7945    0.7229    0.1999    0.5652    0.4904    0.5276    0.1047    0.1634    0.9903    0.5088
    0.1943    0.8625    0.3562    0.4075    0.4936    0.7261    0.2309    0.9519    0.6459    0.0931
    0.2711    0.6464    0.2895    0.1919    0.2751    0.0182    0.3102    0.3679    0.7707    0.2398

>> y=x(:);        %将x按列拉长成一个了列向量
>> hist(y)        %绘制频数直方图
>> xlabel('[0,1]上均匀分布随机数');
>> ylabel('频数');

2.2 常见一元分布随机数

（1） MATLAB统计工具箱中函数名以rnd三个字符串结尾的函数用来生成常见分布的随机数。如下表

函数名说明

binornd 二项分布随机数

chi2rnd 卡方分布随机数

exprnd 指数分布随机数

frnd F分布随机数

lognrnd 对数分布随机数

mnrnd 多项分布随机数

normrnd 正态分布随机数

..................

例：

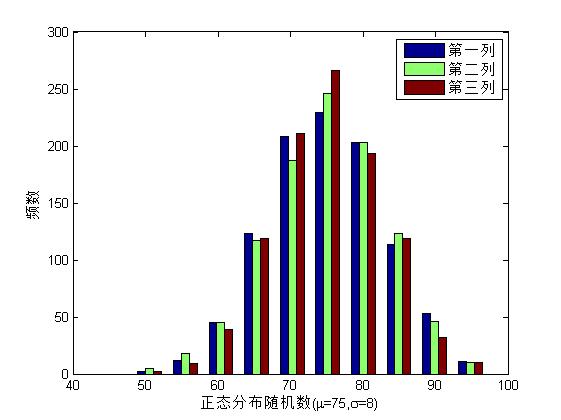
调用normrnd函数生成1000x3的正态分布随机函数，其中均值u=75，标准差为8，并画出各列频数直方图

%调用normrnd函数生成1000行3列的随机数矩阵x，其元素服从均值为75，标准差为8的正态分布
>> x=normrnd(75,8,1000,3);%调用-rnd函数，需要传递给它分布函数的参数，和生成矩阵的维数
>> figure;
>> hist(x); %绘制矩阵x每列的频数直方图
>> xlabel('正态分布随机数(mu=75,sigma=8)');
>> ylabel('频数');
>> legend('第一列','第二列','第三列');

（2）random函数

random函数是一种通用的求各分布的随机数的函数，格式如下：

y=random（‘name’，A1，A2，A3，m，n）

name指定是那种分布函数，取值为1.3中的 MATLAB中常见分布函数列表

A1，A2，A3是分布函数的参数

m，n用来指定生成随机数的行和列

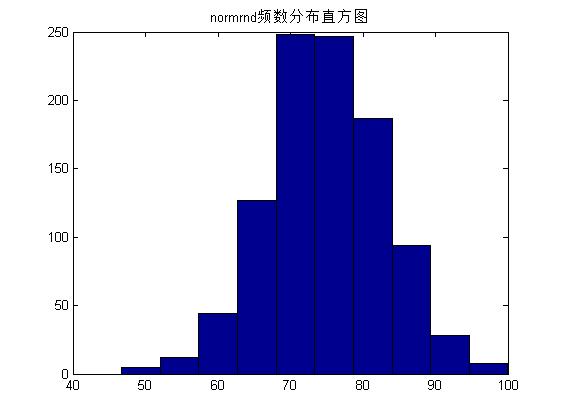
例：用normrnd和random函数分布生成1000x1的正态分布随机函数，其中均值u=75，标准差为8，并画出频数直方图

x=normrnd(75,8,1000,1); %normrnd函数生成均值u=75，标准差为8的正态随机数
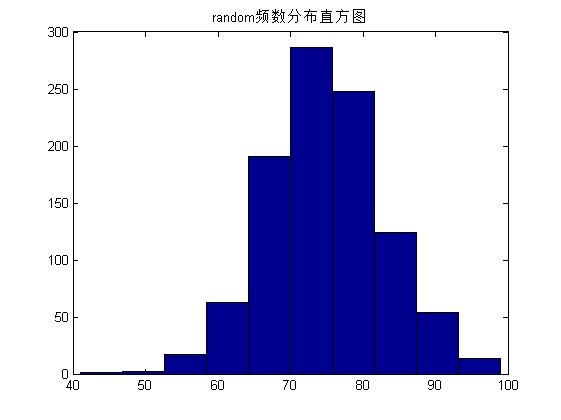
xx=random('norm',75,8,1000,1);%random函数生成均值u=75，标准差为8的正态随机数
figure;
hist(x),title('normrnd频数分布直方图');
>> figure;
>> hist(xx),title('random频数分布直方图');

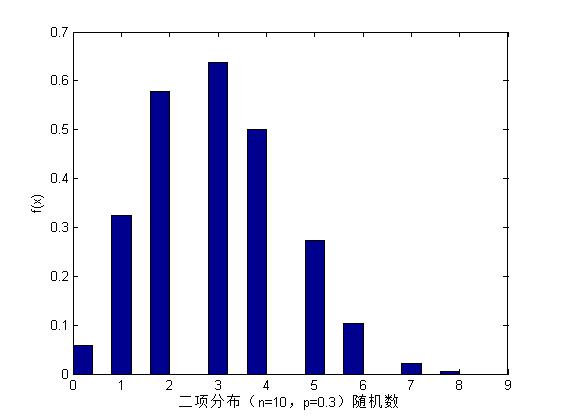
例：调用random函生成1000x1的二项分布随机数向量，然后做出频率直方图。二项分布的参数为n=10，p=0.3

注意：如何计算频率直返图，首先调用ecdf函数就算出经验累积概率分布函数值，然后调用ecdfhist函数绘制频率直方图，其参数是ecdf函数的返回值

%调用random函数生成1000行1列的随机数向量x，其元素服从二项式分布B（10,0.3）
x=random('bino',10,0.3,1000,1);
[fp,xp]=ecdf(x);
ecdfhist(fp,xp,20);%50表示柱状图的个数，默认是10
>> xlabel('二项分布（n=10，p=0.3）随机数');
>> ylabel('f(x)');

2.3 任意一元分布随机数

（1）离散分布随机数

任给一个只取有限个值的离散总体X的分布列

X x1 x2 ...... xn

P p1 p2 ........ pn

由函数randsample函数可以生成服从该分布的随机数。

y = randsample(n,k,true,w)

n表示取值向量

k生成随机数的数量

true：用true表示有放回抽样，false表示不放回抽样

w：取值向量n所对应的概率，与n维度相同

例：设离散总体X的分布列为

X -2 -1 0 1 2

P 0.05 0.2 0.5 0.2 0.05

调用randsample函数生成100个服从该分布的随机数，并调用tabulate函数统计各数字出现的频数和频率

xvalue=[-2 -1 0 1 2]; %定义取值向量
>> xp=[0.05 0.2 0.5 0.2 0.05]; %定义概率向量，与取值向量一一对应
>> %调用randsample函数生成100个服从指定离散分布的随机数

x=randsample(xvalue,100,true,xp);%用true表示有放回抽样，false表示不放回抽样
>> reshape(x,[10,10]) %把向量x装换成10行10列的矩阵，便于观察

ans =

     2     0     1     2     1     0     1     0     1     0
     0     1    -1     0     0    -2     2    -1     0     0
     1     0     0     0     2     0     0    -1    -2     1
     1     1     1     1     0     0     0     0     0     0
     0    -1     1    -2     1     0    -1     0     2     0
     1     0     1    -1     0    -1    -1     0     0     1
     0     2    -1     1    -1    -1    -1     0     0     0
     0     0     1     0     0     0     1     0    -1    -1
     0     0     0     0    -2     0     0    -1    -2    -1
     1     0    -1     0     0    -2     0     0     2     1

>> tabulate(x) %调用tabulate函数统计各数字出现的频数和频率
Value    Count   Percent
     -2        6      6.00%
     -1       17     17.00%
      0       49     49.00%
      1       21     21.00%
      2        7      7.00%

从统计结果看，随机数的频率分布与真实分布差距不大，但并不是完全一样，当生成足够多的随机数时，会越来越接近真实分布。

函数randsrc和randi也可以实现类似的功能。

（2）连续分布随机数

MATLAB统计工具箱中提供了slicesample函数，用来生成任意指定分布随机数

rand=slecesample（initial，nasample，‘pdf’，pdffun）

initial：指定一个初始值

nasample：产生随机数的个数

‘pdf’：概率分布函数

pdffun：概率分布函数的句柄

例：总体X服从抛物线分布，其概率密度函数为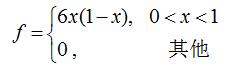，下面调用slicesample函数生成1000个服从该分布的随机数，并画出频率直方图，并与真实的密度函数曲线做比较。

pdffun=@(x)6*x*(1-x);   %用匿名函数方式定义密度函数,pdffun=@(x)6*x*(1-x)*(x>0&x<1)
                        %由于对于x>1或x<0的时候，pdffun<0,密度函不可能小于0，MATLAB会直接
                        %把pdffun=0，所以不需要写成pdffun=@(x)6*x*(1-x)*(x>0&x<1)，但是对于
                        %其它情况下，还是需要指定x的范围的，比如下一个例子
%调用slicesample函数生成1000个服从指定密度函数的随机数
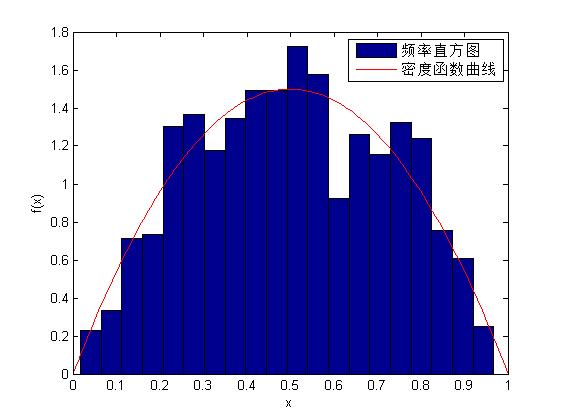
x=slicesample(0.5,1000,'pdf',pdffun);%指定初始值为0.5，需要{pdffun（0.5）>0}
[fp,xp]=ecdf(x); %计算经验累积概率分布函数值
ecdfhist(fp,xp,20); %绘制频率直方图
hold on;
fplot(pdffun,[0 1],'r'); %fplot用来绘制数学函数，plot是针对向量或矩阵的列来绘制曲线的
xlabel('x');
ylabel('f(x)');
legend('频率直方图','密度函数曲线');

例：总体X服从三角分布，其概率密度函数为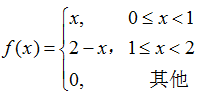，下面调用slicesample函数生成1000个服从该分布的随机数，做出频率直方图，并与真实的密度函数作比较。

pdffun=@(x)x*(x>=0&x<1)+(2-x)*(x>=1&x<2); %密度函数
%调用slicesample函数生成1000个服从该分布的随机数
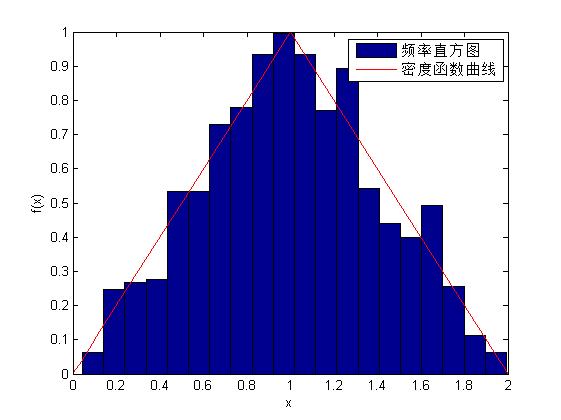
x=slicesample(1.5,1000,'pdf',pdffun);
[fp,xp]=ecdf(x);                        %计算经验累积概率分布函数值
ecdfhist(fp,xp,20);                     %绘制频率直方图
hold on;
fplot(pdffun,[0 2],'r');                %绘制真实密度函数曲线
xlabel('x');
ylabel('f(x)');
legend('频率直方图','密度函数曲线');