泊松分布和指数分布：通俗易懂泊松分布的简易理解指数分布的简易理解总结

87 阅读 0 评论 58 点赞

我是靠谱客的博主瘦瘦草莓，最近开发中收集的这篇文章主要介绍泊松分布和指数分布：通俗易懂泊松分布的简易理解指数分布的简易理解总结，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

传送门 1、泊松分布和指数分布：10分钟教程如果打不开，请点击10分钟！搞懂泊松分布 and 指数分布

2、泊松分布与指数分布的重新理解

泊松分布的简易理解

如果某事件以固定强度λ，随机且独立地出现，该事件在单位时间内出现的次数（个数）可以看成是服从泊松分布。

这个固定强度λ其实就是泊松分布的期望和方差。传送门3、泊松分布的期望和方差推导

举个例子吧：假如我平均每天去超市三次，那我明天会去超市几次？

注意，平均每天去超市三次，并不代表每天一定去超市三次。这里的平均每天去超市三次就是指固定强度λ=3.

因此，我明天可能去超市n次，n=0,1,2,3,……。泊松分布计算器这个计算器默认是单位时间，与时间相关的就直接用λt替换λ~

明天我去超市0次的概率，根据泊松分布可以算出0.0498；

明天我去超市1次的概率，根据泊松分布可以算出0.1494；不大于1次的概率，0.1991

明天我去超市2次的概率，根据泊松分布可以算出0.224；不大于2次的概率，0.4232

明天我去超市3次的概率，根据泊松分布可以算出0.224；不大于3次的概率，0.6472

明天我去超市4次的概率，根据泊松分布可以算出0.168；不大于4次的概率，0.8153

明天我去超市5次的概率，根据泊松分布可以算出0.1008；不大于5次的概率，0.9161

概率分布函数简称分布函数。传送门4、Richard Xu 怎样通俗地理解分布函数？

概率密度函数简称概率密度。传送门5、Counterbalance概率密度函数在某一点的值有什么意义？

概率分布函数和概率密度函数的进一步理解。传送门6、应该如何理解概率分布函数和概率密度函数？

泊松分布的图形大概是下面的样子。这个图是传送门1中的图形，该图形中，固定时间长度（单位时间）与纵坐标的乘积就表示概率。所有的柱状图的面积相加为1。

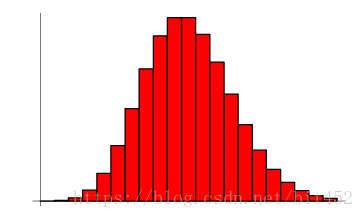
matlab中的概率统计函数，传送门7、MATLAB概率统计函数(1)

matlab下泊松分布绘图代码

 x=0:1:10
 px=poisspdf(x,3); %λ=3 生成泊松分布的概率密度函数
 plot(x,px)
 y=poisscdf(x,3);  %λ=3 生成泊松分布的概率分布函数
 plot(x,y)

固定强度λ=3的泊松概率分布函数图形如下:

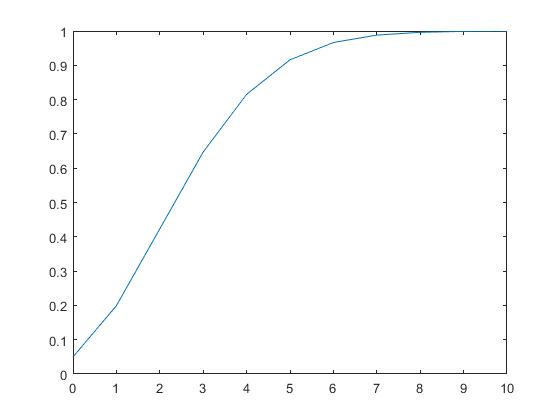
（概率）分布函数还有一个更好理解的名字，叫做累积分布函数(Cumulative Distribution Function)。累积理解起来有点不爽，我一般是记成累计~一个意思，理解就好。根据分布函数，可以较直观的看出，去超市不大于n次的概率。

固定强度λ=3的泊松概率密度函数图形如下:

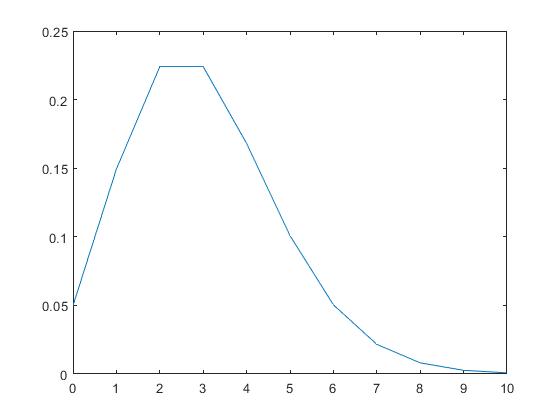
某一点的概率密度大，说明在这一点附近发生的概率相对于其他点发生的概率大。注意，概率密度是可以大于1的，假如说某一点的概率密度为100，但是这一点附近指的是，这一点的区间长度可能会远远小于0.001.因此这一点附近发生的概率大概是0.1=100x0.001，概率密度与x轴围成的面积是1，也就是说，所有事件发生的概率和为1。这里面涉及到微积分中的积分问题，感兴趣的可以去看下微积分中积分的物理意义~

一般地，离散型随机变量的分布函数为阶梯函数。传送门8、怎样理解离散型随机变量分布函数的右连续性？

我的例子是离散型的随机变量，但是我做的图是连续型的随机变量的概率分布函数和概率密度函数，所以例子和图不匹配。

曾经的我以为世界非黑即白，硬币只有正反两面。

初中的我知道了硬币的正面和反面的概率都是0.5。（离散）

再后来我知道了，世界并不是非黑即白，还有灰色。从白（255）到黑（0），是可以用灰度来衡量的。（连续）

人可以被分成好人和坏人。概率密度函数类似于灰度。

人的一生很长，某人在某一点的概率密度函数很大，灰度很大（255），但是持续的时间很短，说明这个人在那段时间表现出来的是个好人。这或许也是理解概率密度函数的一种方法。

小的时候我评价别人的时候说，他是好人。我现在会说，他很可能是好人（较大的概率）。概率论让我中毒不浅~

传送门9、泊松分布的现实意义是什么，楚小鱼

注意Poisson还有一个知名度比较小的第二个定义，或者说是Poisson Process的定义：假定一个事件在一段时间内随机发生，且符合以下条件：

（1）将该时间段无限分隔成若干个小的时间段，在这个接近于零的小时间段里，该事件发生一次的概率与这个极小时间段的长度成正比。
（2）在每一个极小时间段内，该事件发生两次及以上的概率恒等于零。
（3）该事件在不同的小时间段里，发生与否相互独立。
则该事件称为poisson process。

泊松分布的用途:

某人一天内收到的微信的数量
来到某公共汽车站的乘客
某放射性物质发射出的粒子
显微镜下某区域中的白血球

指数分布的简易理解

传送门：10、如何理解指数分布的无记忆性？

11、指数分布的定义形式及应用

指数分布是一种连续概率分布。

指数分布和泊松分布是有关系的：

指数函数的无记忆性来自于泊松过程k=0时的时间指数性，而泊松过程k=0时的时间指数性来自于泊松分布时 lambda的恒定性，也就是离散情况下，二项分布的n*p的恒定性。

传送门12、指数分布的期望和方差推导

指数分布的用途：

指数分布可以用来表示独立随机事件发生的时间间隔，比如旅客进机场的时间间隔、中文维基百科新条目出现的时间间隔等等
在排队论中，一个顾客接受服务的时间长短也可以用指数分布来近似。
无记忆性的现象（连续时）

举个例子吧，假设我平均每三天去超市一次，服从指数分布。

那么我平均每天去超市1/3次。 λ就表示平均每单位时间发生该事件的次数，是指数函数的分布参数。此处的λ=1/3。

那么，指数分布概率分布是解决什么问题呢。

我今天去了超市，那么

我隔了1天没有去超市的概率，根据指数分布可以算出0.7165，隔了1天就又去了超市的概率，根据指数分布可以算出0.2835；

我隔了2天没有去超市的概率，根据指数分布可以算出0.5134，我在2天内去了超市的概率，根据指数分布可以算出0.4866；

我隔了3天没有去超市的概率，根据指数分布可以算出0.3679，我在3天内去了超市的概率，根据指数分布可以算出0.6321；

我隔了4天没有去超市的概率，根据指数分布可以算出0.2636，我在4天内去了超市的概率，根据指数分布可以算出0.7364；

我隔了5天没有去超市的概率，根据指数分布可以算出0.1889，我在5天内去了超市的概率，根据指数分布可以算出0.8111；

（计算方法使用的是MATLAB中的expcdf函数，此处需要注意的是，expcdf函数的第二个参数是指数函数的期望值，此处λ=1/3，期望值为3，也就是说，我预期隔了3天会去超市1次。）

matlab下指数分布绘图代码

x=0:1:10;
ex=expcdf(x,3);%这里的第二个参数是均值（期望），指数分布的概率分布函数
plot(x,ex)
ey=exppdf(x,3);%指数分布的概率密度函数
plot(x,ey)

λ=1/3（期望为3）的指数分布概率分布函数图形如下:

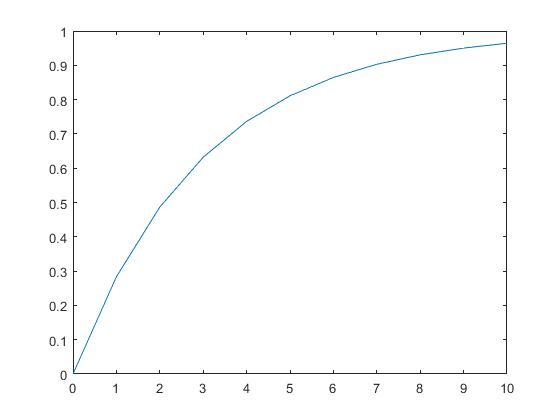
从图中可以看出，我今天去了超市，那么我在10天内去了超市的概率都还没到1。

因为银行排队论中，一个顾客接受服务的时间长短也可以用指数分布来近似，所以说，哪怕银行雇员告诉你，我们平均每10分钟就能服务完1个顾客，你也要做好排队2个小时的思想准备~~~~

λ=1/3（期望为3）的指数分布概率密度分布函数图形如下:

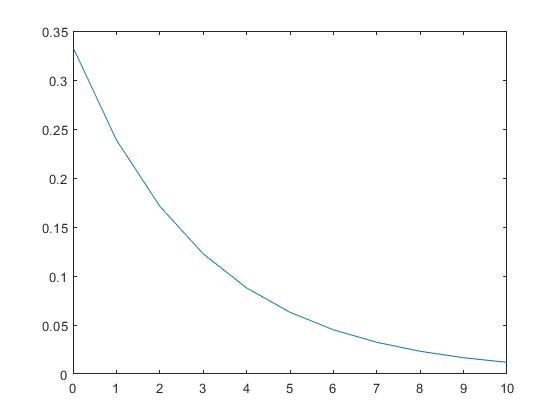
因为银行排队论中，一个顾客接受服务的时间长短也可以用指数分布来近似，所以说，哪怕银行雇员告诉你，我们平均每10分钟就能服务完1个顾客，我们也要做好排队2个小时的思想准备，但是根据指数分布概率密度来看，我们排队2个小时才被服务的概率密度还是比较低的，因此排队2个小时左右（一个时间段）的概率也是比较低的。注意：概率密度和概率的不同。