文章目录
- 标准柯西分布
- 标准指数分布
- 标准伽马分布
- 标准正态分布
- 标准学生分布
np.random中提供了下面五种标准分布
| 函数 | 分布 |
|---|---|
| standard_cauchy() | 标准柯西分布 |
| standard_exponential() | 标准指数分布 |
| standard_gamma(k) | 标准伽马分布 |
| standard_normal() | 标准正态分布 |
| standard_t(df) | 标准学生分布 |
标准柯西分布
标准柯西分布的概率密度表达式为
P ( x ) = 1 π ( 1 + x 2 ) P(x)=frac{1}{pi(1+x^2)} P(x)=π(1+x2)1
import matplotlib.pyplot as plt
import numpy as np
x = np.random.standard_cauchy(size=1000)
plt.hist(x,100,range=(-10,10))
plt.show()
效果为
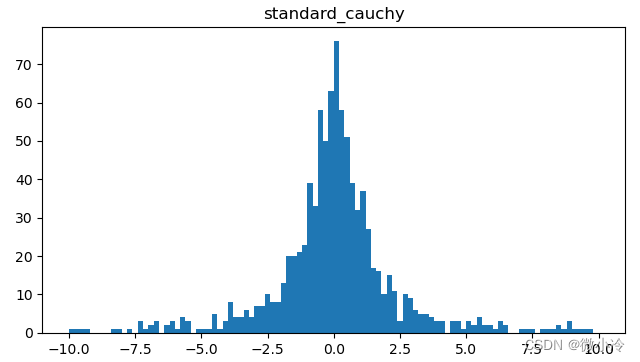
标准指数分布
标准指数分布的概率密度表达式为
P ( x ) = exp − x P(x) = exp-x P(x)=exp−x
x = np.random.standard_exponential(size=1000)
plt.hist(x,100)
plt.title("standard_exponential")
plt.show()
效果为
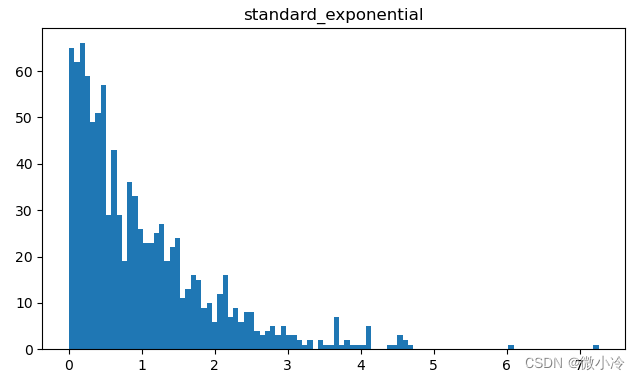
标准伽马分布
标准伽马分布的概率密度表达式为
P ( x ) = x k − 1 e − x Γ ( k ) P(x) = x^{k-1}frac{e^-x}{Gamma(k)} P(x)=xk−1Γ(k)e−x
其中 Γ Gamma Γ表示伽马函数,为阶乘函数的解析延拓,当 k k k为整数时, Γ ( K ) = k ! Gamma(K)=k! Γ(K)=k!
x = np.random.standard_gamma(size=1000)
plt.hist(x,100)
plt.title("standard_gamma")
plt.show()
其分布图为
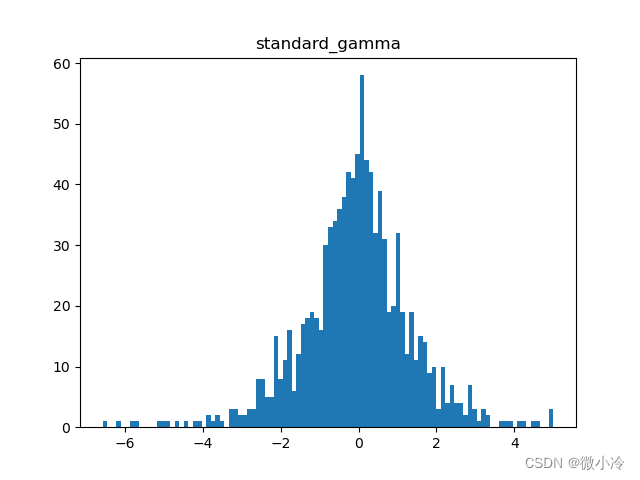
标准正态分布
标准正态分布即为中心在 x = 0 x=0 x=0,标准差为1的正态分布,其概率密度表达式为
P ( x ) = e − x 2 P(x) = e^{-x^2} P(x)=e−x2
x = np.random.standard_normal(size=1000)
plt.hist(x,100)
plt.title("standard_normal")
plt.show()
其分布图为
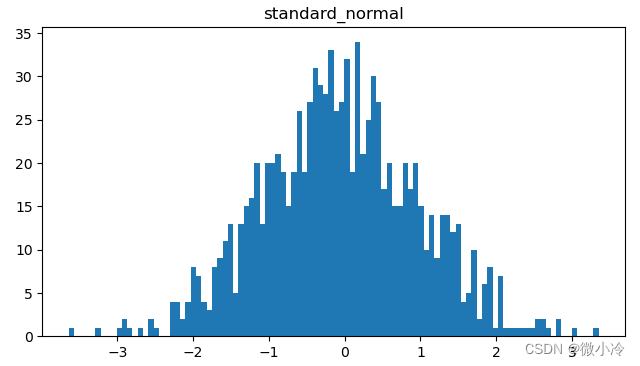
标准学生分布
标准学生分布的概率密度表达式相对比较复杂,而且还包括一个参数df
P ( d f , x ) = Γ ( d f + 1 2 ) π d f Γ ( d f 2 ) ( 1 + x 2 d f ) − d f + 1 2 P(df,x) = frac{Gamma(frac{df+1}{2})}{sqrt{pi df}Gamma(frac{df}{2})}(1+frac{x^2}{df})^{-frac{df+1}{2}} P(df,x)=πdfΓ(2df)Γ(2df+1)(1+dfx2)−2df+1
x = np.random.standard_t(df=1, size=1000)
plt.hist(x,100, range=(-50,50))
plt.title("standard_t")
plt.show()
其分布图为
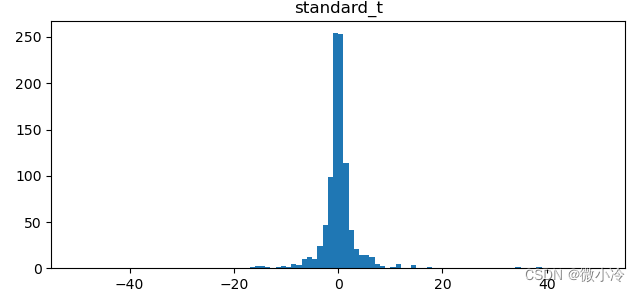
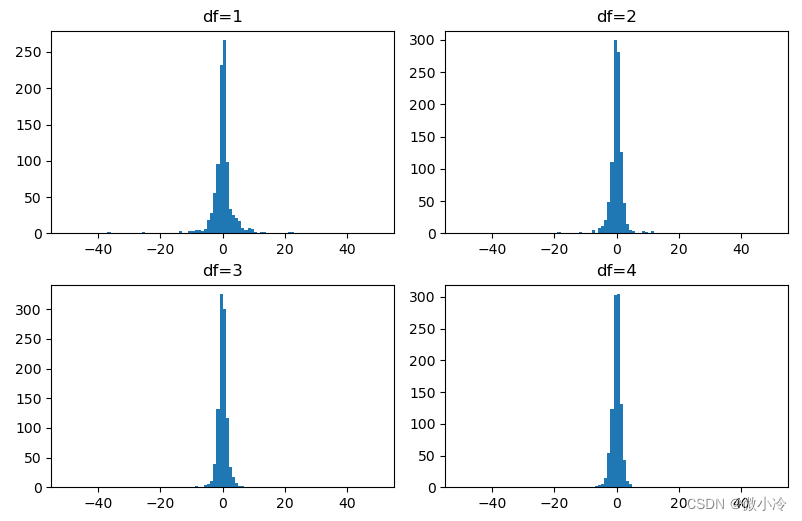
接下来可以看一下,当df取值不同时分布情况的变化
fig = plt.figure("standard_t")
for i in range(4):
ax = fig.add_subplot(2,2,i+1)
x = np.random.standard_t(df=i+1, size=1000)
ax.hist(x, 100, range=(-50,50))
ax.set_title(f"df={i+1}")
plt.show()
最后
以上就是可耐钥匙最近收集整理的关于【Python】Numpy中提供的五种标准随机分布详解的全部内容,更多相关【Python】Numpy中提供内容请搜索靠谱客的其他文章。



![triplus在matlab字函数,[理学]第7章 MATLAB在信号处理中的应用.ppt](https://www.shuijiaxian.com/files_image/reation/bcimg10.png)




发表评论 取消回复