一 卡诺图化简性质
性质1: 深蓝色文字诺图中两个逻辑相邻的1方格的最小项可以合并成一个与项, 消去一个变量。
要注意的是: 逻辑相邻不仅仅是几何位置上的相邻,最左边的列与最右边的列、最上面的行和最下面的行都是逻辑相邻的。
性质2:卡诺图中四个逻辑相邻1方格的最小项可以合并成一个与项,并消去两个变量。
性质3:卡诺图中八个逻辑相邻的1方格可以合并成一个与项,并消去三个变量。
二 卡诺图化简步骤及举例
步骤包括:
(1)画出函数的卡诺图;
(2)仔细观察卡诺图,找出 ![]() 个逻辑相邻的1方格,并给它们画上圈,画圈的原则要使圈尽可能大;
个逻辑相邻的1方格,并给它们画上圈,画圈的原则要使圈尽可能大;
(3)按照卡诺图化简性质,写出最简与或表达式。
以下看几个例子
例1 用卡诺图化简函数F(A,B,C,D) = ![]() 。
。
解: (1)画出函数F的卡诺图。
把逻辑函数写成最小项形式如下:
原式等于 F(A, B, C, D) = m3+m9+m11+m13
=![]()
画出该函数的卡诺图如下图(a) 所示
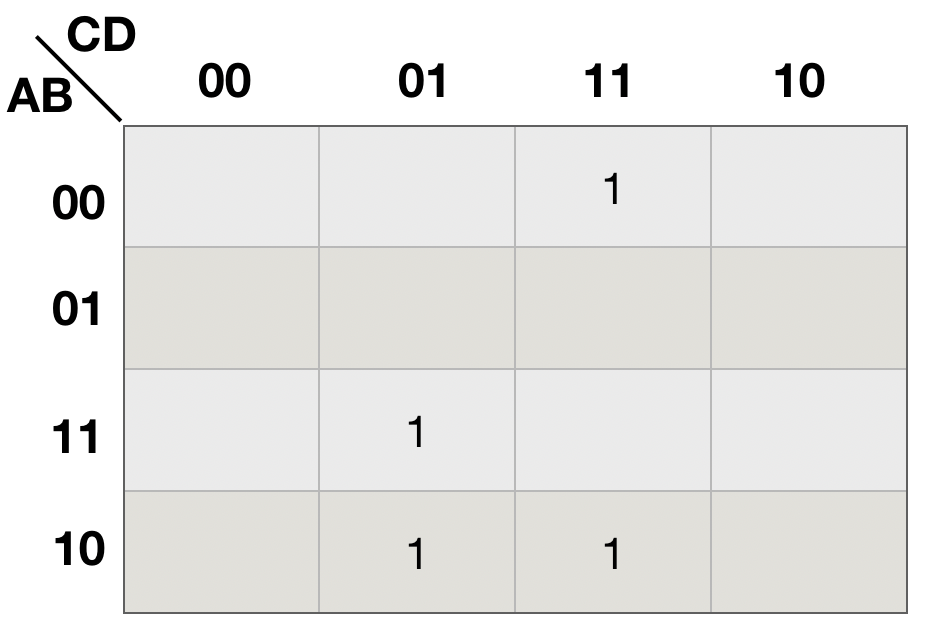
(a) (b)
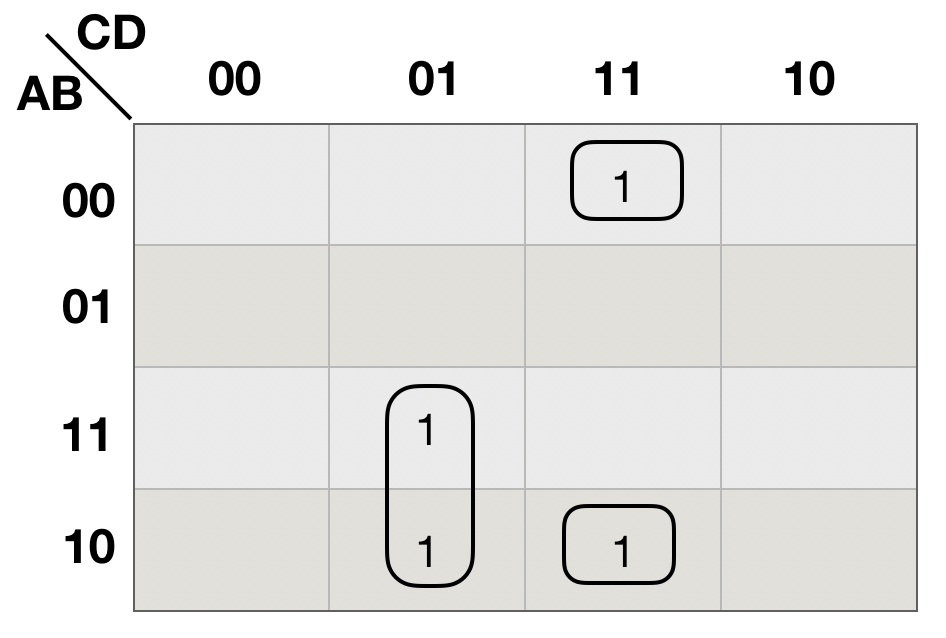
(2)给逻辑相邻的1方格画圈
按照逻辑相邻原则画圈, 如上图(b)所示。
(3)按照卡诺图化简性质,写出两个圈的最简与或表达式,并把它们相或起来, 就得到该逻辑函数的最简与或表达式。
![]()
例2: 用卡诺图化简下列函数,并写出最简与或表达式: ![]()
解: 分几步来解析
(1)画出函数F的卡诺图
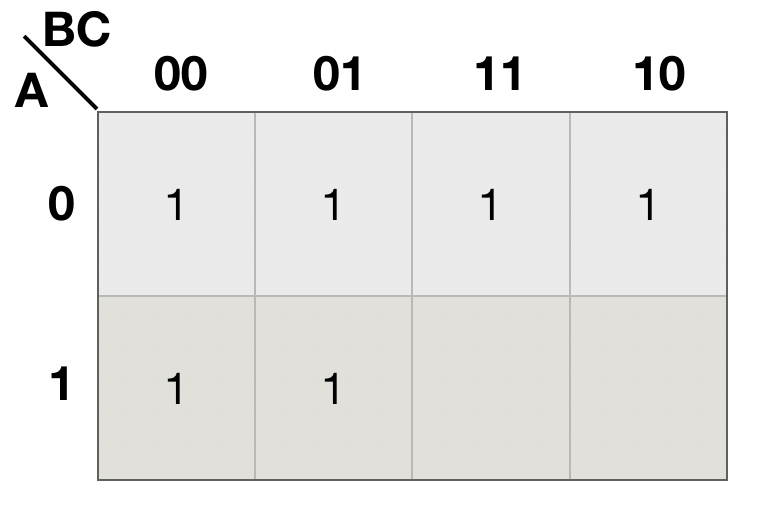
(2) 给逻辑相邻的1方格画圈,按照逻辑相邻原则画圈。
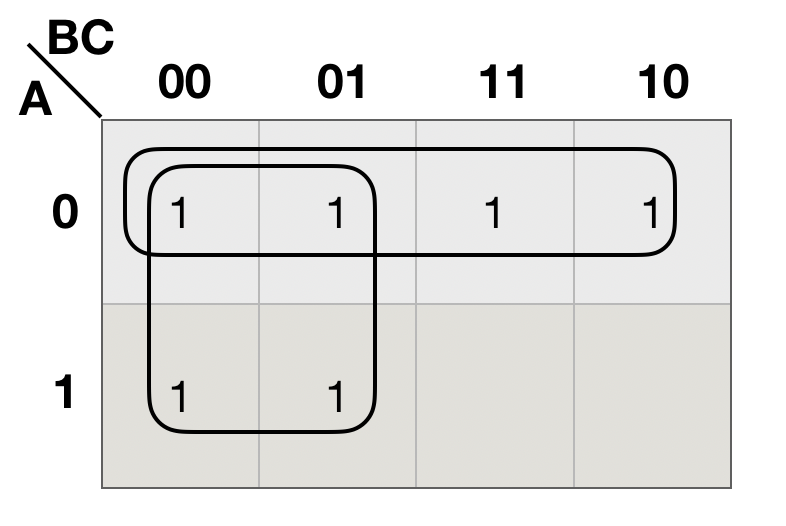
(3)按照卡诺图化简性质,画出两个圈的与或表达式,并把它们相或起来,就得到最简与或表达式
![]()
本例的画圈,我还是存有疑问的,横圈是否可以只圈最后两格, 不是圈住4格?
在做卡诺图化简要注意事项: 在卡诺图上画圈有几个问题:
(1)将卡诺图中的1方格画圈, 一个也不能漏掉,1方格允许被多次圈用。
(2)圈的个数应尽可能少,因为一个圈和一个与项相对应,圈数越少, 与或表达式的与项就越少。
(3)圈内的1方格数必须为![]() 个,圈的范围越大越好,因为圈越大,可消去的变量就越多,与项中的变量就越少。
个,圈的范围越大越好,因为圈越大,可消去的变量就越多,与项中的变量就越少。
(4)每个圈应至少包含一个新的1方格, 否则这个圈就是多余的。
(5)在同一个卡诺图中画圈的方式可能不是惟一的,因此用卡诺图化简所得到的最简与或表达式也不是惟一的。
这里特别提醒注意 第4点, 看一个图加强理解
用卡诺图化简函数F(A,B, C, D)=![]() , 画图为
, 画图为
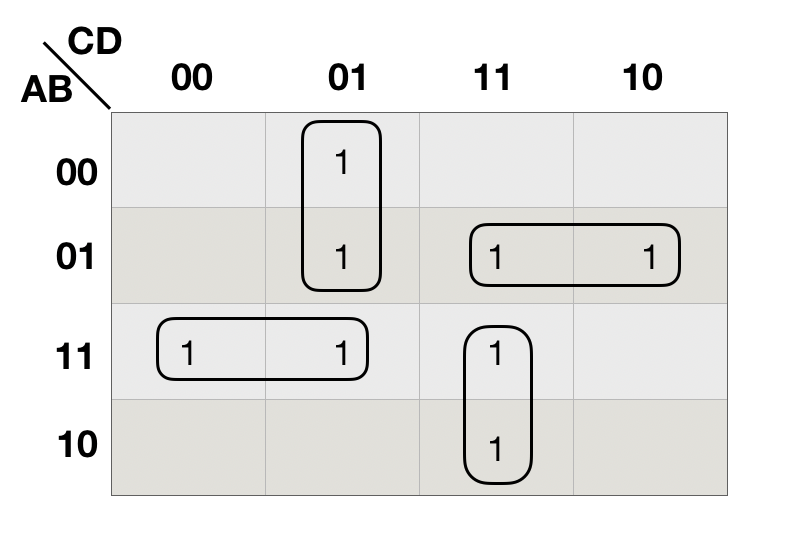
这里绝不能给中间4个1方格 画圈, 因为没有新的1方格,都已被圈过!
最后
以上就是激昂小松鼠最近收集整理的关于电子技术基础(三)__第5章 之逻辑函数的卡诺图化简方法的全部内容,更多相关电子技术基础(三)__第5章内容请搜索靠谱客的其他文章。



![[转] 基本RS触发器](https://www.shuijiaxian.com/files_image/reation/bcimg1.png)




发表评论 取消回复