基于两相静止坐标系上的状态方程的感应电动机起动动态计算matlab程序
1 静止两相正交坐标系中的动态数学模型
1.1 定子绕组和转子绕组的3/2变换
对静止的定子三相绕组和旋转的转子三相绕组进行相同的3/2变换,变换后的定子两相正交坐标系静止,而转子两相正交坐标系以角速度逆时针旋转。

1.2 电压方程

1.3 磁链方程

1.4 转矩方程

2 静止两相正交坐标系中的状态方程
三相感应电机在三相坐标系上的状态方程是8阶方程,其中6阶电压方程、1阶运动方程和1阶转角方程由前述两相坐标系中的动态方程可见,如果不计零序分量,两相坐标系上的电压方程为4阶,加上1阶运动方程,其状态方程降为5阶,由于电感矩阵与转角6无关,转角方程可以不必列于联立求解的微分方程组感应电机的状态方程可以建立在不同的两相坐标系上,而且状态变量也有不同的选取方法,除了转速作为必选的状态变量外,其余4个状态变量可以在两相定子电流、两相转子电流、两相定子磁链、两相转子磁链这4组变量中任意选取两组。
将两相静止坐标系上的磁链方程代入到电压方程中,写成矩阵形式可得:

其中:
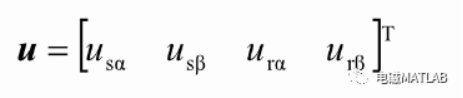




则
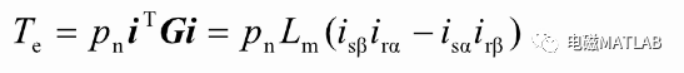

整理得:

3 算例
电机参数如下:f=50;Un=220;Rs=2.68;Rr=2.85;LAA=0.265;Laa=0.265;Lms=0.253;pn=2;J=0.02;ROmega=0;TL=0;
4 程序运行结果
电流

转矩

转速-转矩

5 matlab程序
clc
clear
close all
%% 参数
f=50;
Un=220;
Rs=2.68;
Rr=2.85;
LAA=0.265;
Laa=0.265;
Lms=0.253;
pn=2;
J=0.02;
ROmega=0;
TL=0;
%计算两相坐标系电感
Lm=3*Lms/2;
Ls=LAA-Lms+Lm;
Lr=Laa-Lms+Lm;
%% 计算电感矩阵L
L=[ Ls,0,Lm,0;
0,Ls,0,Lm;
Lm,0,Lr,0;
0,Lm,0,Lr ];
%% 电阻矩阵
R=[Rs,0,0,0;
0, Rs,0,0;
0,0,Rr,0;
0,0,0,Rr ];
%% 计算G矩阵
G=[0,0,0,0;
0,0,0,0;
0,Lm,0,Lr;
-Lm,0,-Lr,0 ];
%% 计算L的逆
L_INV=inv(L);
%% 仿真
y0=zeros(5,1);
TF=0.35;
options=odeset('RelTol',1e-3,'AbsTol',1e-4,'MaxStep',1e-3);
%调用变步长龙格库塔法ode45求解
[T,Y]=ode45(@IM_Model_2ph,[0,TF],y0,options,f,Un,R,L_INV,G,pn,J,ROmega,TL);
%% 结果输出
is_alpha=Y(:,1);
is_beta=Y(:,2);
ir_alpha=Y(:,3);
ir_beta=Y(:,4);
%计算转矩
Te=pn*Lm*(is_beta.*ir_alpha-is_alpha.*ir_beta);
%画图
iA=sqrt(2/3)*is_alpha;
Omega=Y(:,5);
n=Omega/pn*30/pi;
h=figure('Position',[520,380,500,300],'Name','Stator Current iA');
plot(T,iA)
xlabel('时间')
ylabel('电流')
h=figure('Position',[5,5,500,300],'Name','Torque Te');
plot(T,Te)
xlabel('时间')
ylabel('转矩')
h=figure('Position',[520,5,500,300],'Name','Torque vs Speed Te-n');
plot(n,Te)
xlabel('转速')
ylabel('转矩')
。。。。。。略
最后
以上就是丰富啤酒最近收集整理的关于基于两相静止坐标系上的状态方程的感应电动机起动动态计算matlab程序的全部内容,更多相关基于两相静止坐标系上内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复