目录
卷积神经网络结构图
为什么从神经网络到卷积神经网络?
卷积
解决上述问题:
卷积过程
卷积多通道处理
池化
全连接层
使用TensorFlow框架简单实现CNN(手写数字识别)
卷积神经网络结构图

上图就是一个典型的卷积神经网络,卷积神经网络 = 卷积 + 池化 + 全连接
为什么从神经网络到卷积神经网络?
普通的神经网络,最经典的那种神经网络模型图也就是多个输入,一层隐藏层,后面接输出层。
那么普通的神经网络(BP神经网络)在对图像进行处理的时候,会像下图一样:
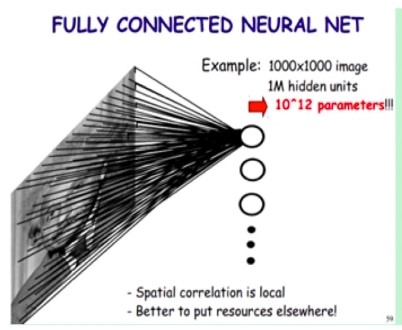
假设图片是 1000 * 1000像素的,有一层隐藏层,隐藏层的大小是 10 ^ 6,那么我们的参数大小有 10 ^ 12。
第一个问题:这种程度大小的参数对于我们机器的内存和计算量来说是巨大的,分分钟扛不住。
第二个问题:除了硬件上的开销太大,参数过多会导致过拟合,由于模型的参数太多,模型的表达能力太强,它会尽可能记住模型中的每个样本
(过拟合:模型在训练集上表现非常不错,到了测试集就不能很好的预测)
卷积
解决上述问题:
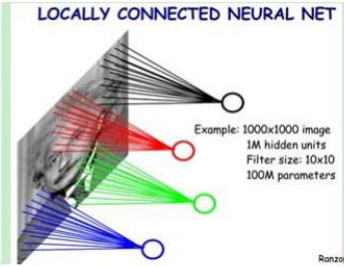
卷积层两大特点:
局部连接
对于一张图片而言,也就是上面这张图片,像素点和它周围的像素点的值会比较有联系,比如红色区域中,眼睛和眉毛的像素点的关联非常大,而眼睛和绿色区域的嘴巴的关联性不那么大。所以图片的数据有较强的区域性。所以我们可以将每个神经元和每个图像特征的全连接改成局部连接。
如上面那个图显示的一样,每个神经元只和一部分的像素点进行连接,比如他这里有 10 ^ 6个神经元,每个神经元只和 10 * 10的像素点进行连接,那么就有 10 ^ 8 比起一开始的时候少很多。为了不影响下面的理解这里说细一点,也就是每一个神经元都是 10 * 10, 有10 ^ 6个神经元 10 * 10 * 10 ^ 6 = 10 ^ 8个参数,但此时每个神经元内的参数和其他神经元参数是不一样的。
共享参数
图像特征和图像位置无关:比如一个苹果可能出现在相片的任何位置
比如所我们现在的目标是找一张图片内的苹果,因为原本一个神经元会和整张图片去做连接,也就是相当于,它会将整张图片扫一遍,那么是可以找到苹果的,我们现在引出一个问题,就是我们现在每个神经元只和局部的 10 * 10 像素范围的局部图片做连接,那么在这个范围内,是有可能不包含苹果的,那么我们捕捉不到苹果特征。
这时候我们引入参数共享的概念:
让每个神经元和局部图片的连接都采用同样的参数,也就是卷积核
有什么好处:
假设用一个 10 * 10 的卷积核
1. 降低模型参数,每个神经元共享一个卷积核参数,那么我们的 10 ^ 2的参数,和之前10 ^ 12个参数相比,降低了非常多。
2.
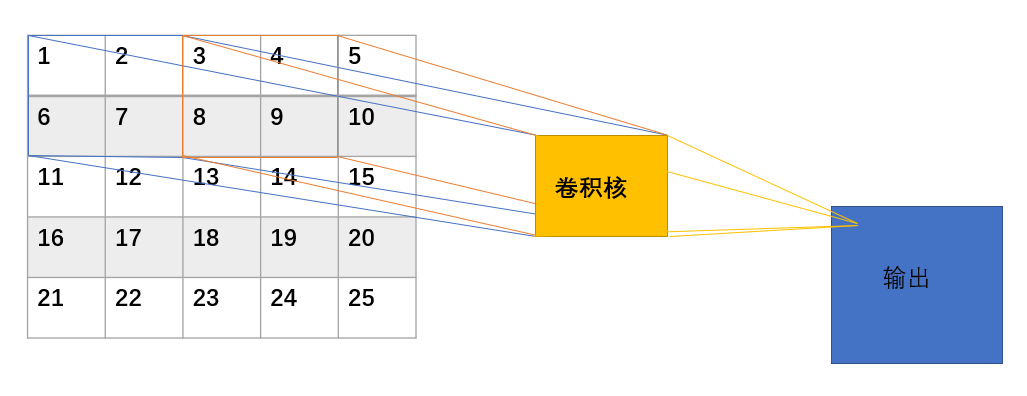
(画的有点丑,见谅)
那么我们的卷积核从图片上滑过,从左到右,从上到下,每个区域都和卷积核计算出来一个值放在输出的一个地方,每个值可以代表一个神经元,那么一整张图片我们不知道我们要捕捉的特征在哪,那么假设我们的特征在上图中的左上角,也就是蓝色方框内,那么我们在右侧的输出的左上角对应的那个神经元被激活,若是图像特征在橙色的区域,那么我们右侧的最上面的第二个神经元被激活,也就是不管图像在哪,都会被卷积核捕捉放到某个神经元上。
这也就是为什么卷积层往往会有多个卷积核(甚至几十个,上百个),因为权值共享后意味着每一个卷积核只能提取到一种特征,为了增加CNN的表达能力,当然需要多个核
卷积过程
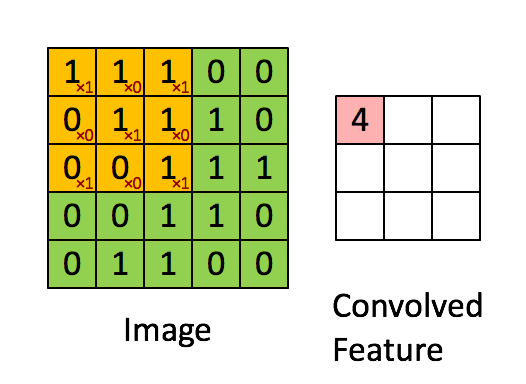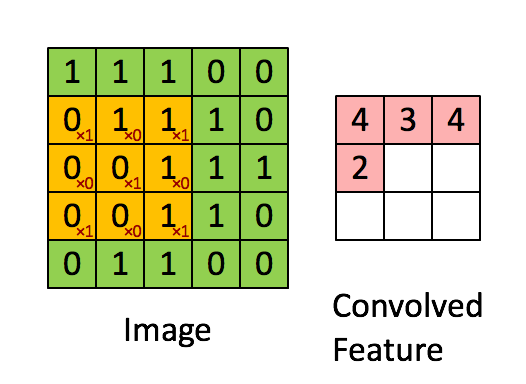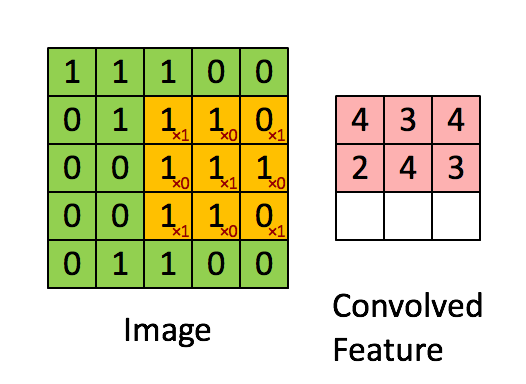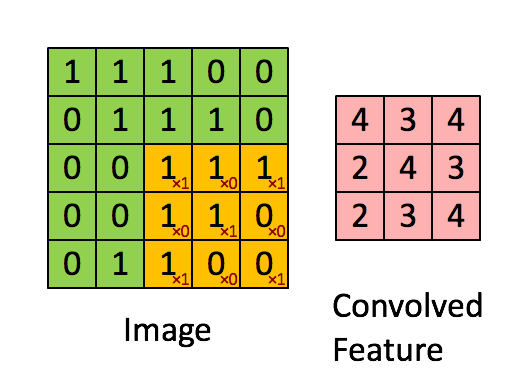
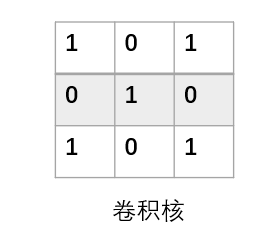
好吧我从网上找了个很清晰的流程图,让大家可以更好的理解上图的卷积核在右侧
ok,那么我们来看输出的大小和原图大小的关系: 输出大小 = 图片大小 - 卷积核大小 + 1 (上图举例: 3 = 5 - 3 + 1)
步长
控制每一次滑动在图像上移动多少,上图的步长就是1,也就是每一次往右移1,若步长是2的话就向右移2
问题:每次图像都变小一层,对于实际运算的时候可能是比较麻烦的
为了解决这个问题,我们可以在图像的外层padding一圈0,让他输出的大小和原图大小一致。
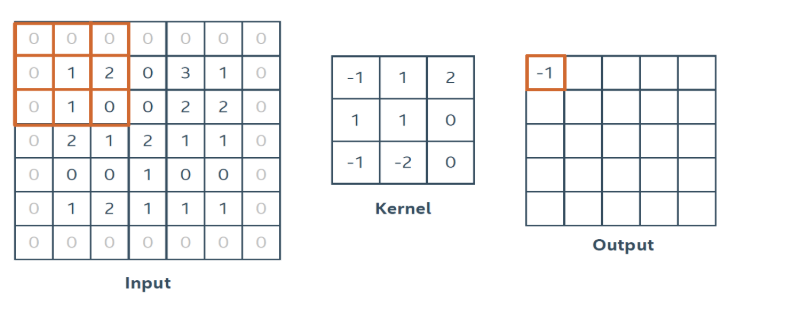
就向上图这样子,非常好理解就不解释了
卷积多通道处理
上面讲的都是卷积单通道的处理比如说灰度图,每个像素由一个值表示,下面我们来研究一下卷积如何处理多通道
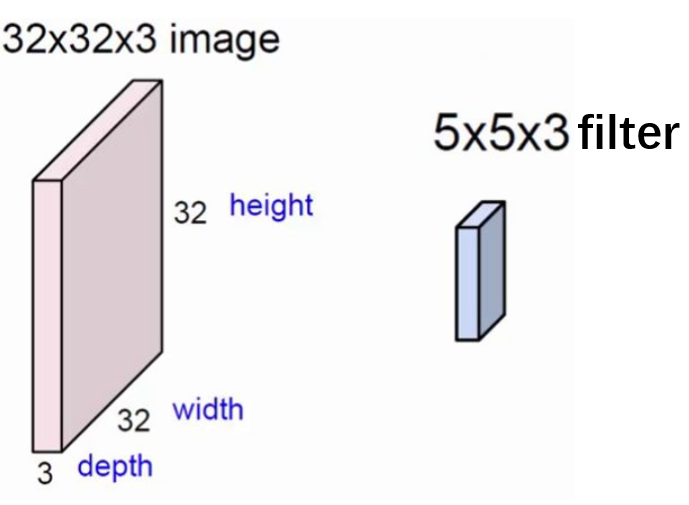
左侧是一个多通道的图, 我们将右侧的蓝色的卷积核也变为多通道的,每个通道 5 * 5,每个通道的卷积的参数是不共享的,一般来说也可以描述成尺寸 5 * 5,深度为3的filter。
接下来我们用这三个通道每个通道的卷积参数和相应通道的图片输入做内积,然后将卷积核三个通道对应得到的结果想加起来作为输出神经元的值,如下图的过程
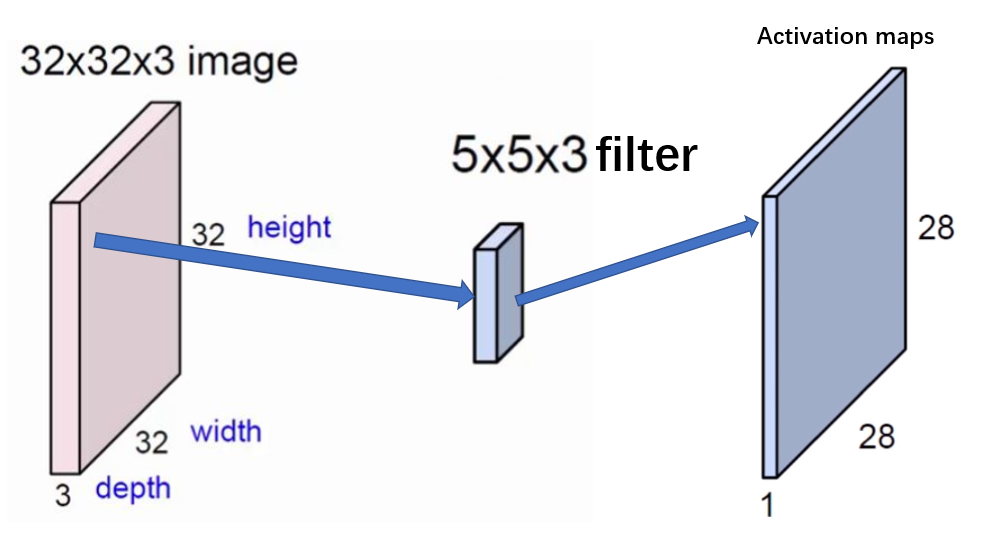
这样子经过从左到右从上到下的卷积之后这一个卷积核就可以生成右侧的这一张特征图,也就是一个通道的图。那么我们如何生成多个输出神经元的图呢:
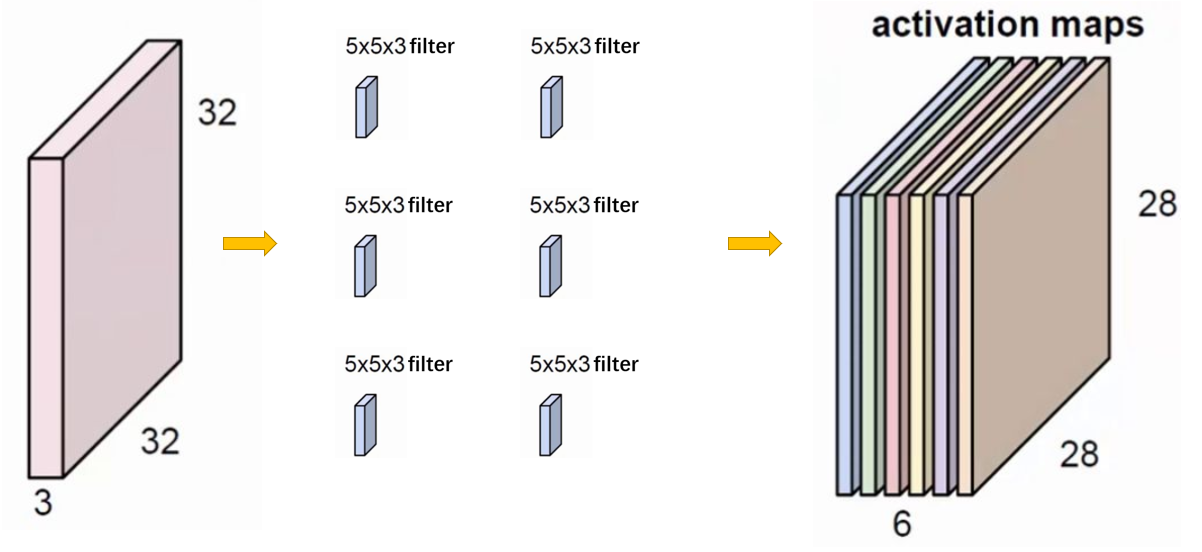
多加几个卷积核,这些卷积核参数不共享,那么我们用六个卷积核就可以得到六个输出图。
卷积核其实用来提取某种特征,我们采用多个卷积核就可以提取多个图像特征。
但是和卷积核计算完内积之后这个计算并没有结束,我们还需要使用激活函数:
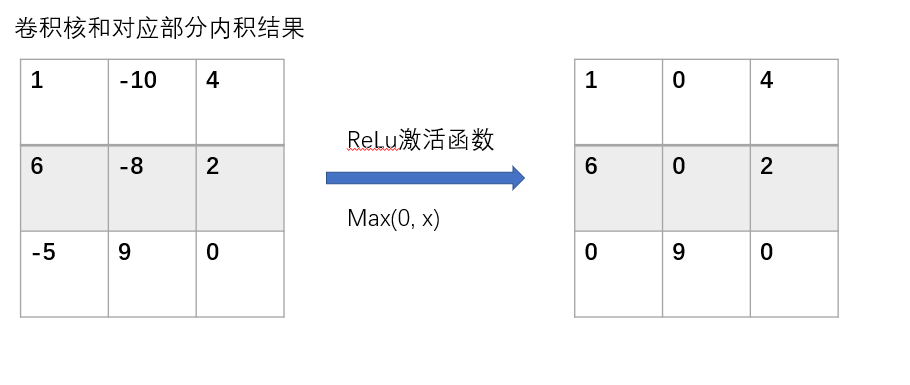
卷积通常使用的激活函数是ReLu
池化
池化就是对特征图进行特征的特征压缩,也叫做亚采样,选择一个区域的max值或者mean值来代替该区域,就实现了一个特征压缩的效果。
最大值池化——Max Pooling
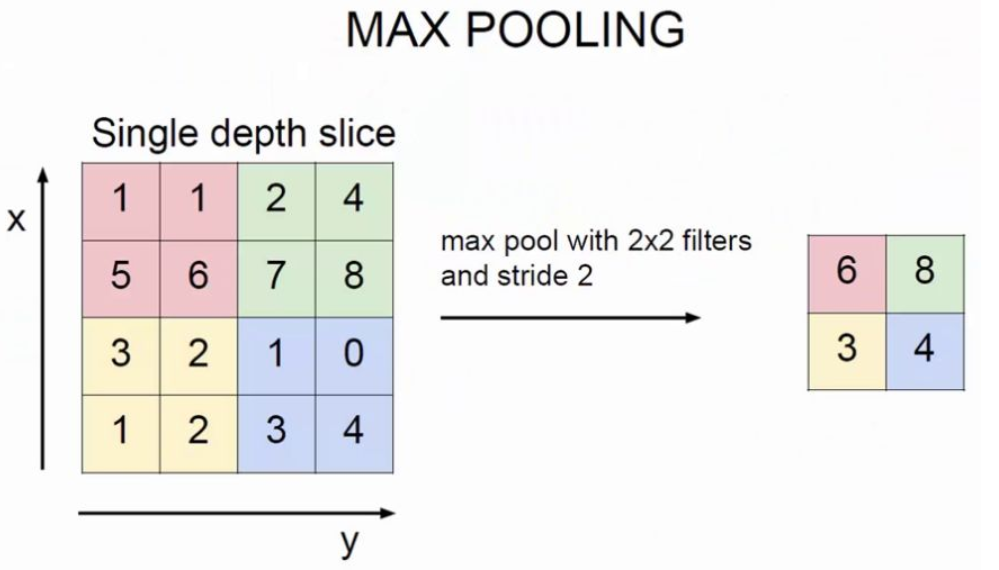
这个过程也是有一个窗口类似卷积那种从左到右从上到下的滑动,有一点不一样的是他的步长一般是和窗口的宽度一致的,若是滑动到右边有多余的列,有两种处理方法:padding(上面介绍过)和舍弃,一般来说会采用舍弃。
max-pooling:取filter覆盖区域的最大值
平均值池化
滑动过程和最大池化一致,只是取filter覆盖区域的平均值
池化的特性
一、不重叠
设置的步长和窗口的宽度一直,窗口滑过是不会出现重叠的
二、减少图像的尺寸减少计算量
三、可以解决平移鲁棒
什么是平移鲁棒:

假设上面蓝色区域是一个图片,橙色区域是我们的图片特征,那么我们的图片特征稍微的往旁边挪动一点,就会变成下图的样子

那么橙色区域和蓝色区域通过最大池化的出来的结果可能是一样的,那么平移前和平移后的结果可能是一样的,池化可以一定程度上解决这种平移问题。
四、降低了空间精度
因为池化的过程会损失几个值,所以一定程度上会损失一些精度,让图像特征更具体,表达能力更好,减少不重要的特征。
一定程度上防止过拟合。
全连接层
将上一层的输出展开到每一个神经元上也就是普通的神经网络层。
全连接层后面可以再接全连接层,但是不能再接池化,因为已经不是多维的图片信息了
使用TensorFlow框架简单实现CNN(手写数字识别)
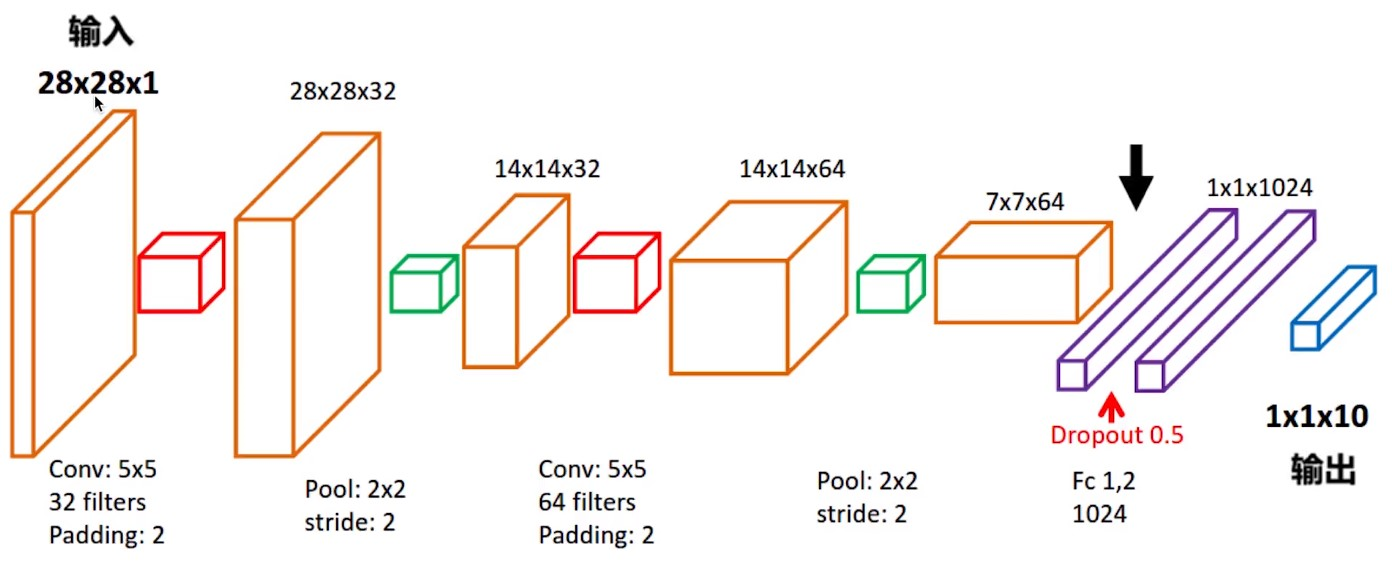
手写数字识别就是有非常多张黑白的手写数字图片,给CNN进行学习,然后从测试集上抽取几张图片输入训练完的模型中,训练完的模型会给出它自己识别的数字是多少,和正确的结果进行比对并输出准确率,这是一个基本流程,下面是流程图:
最终想要的效果:
每一张手写数字图片都是 28 * 28 * 1,因为不是RBG的
经过一层卷积,32个filters,变成 28 * 28 * 32。每个filter都会像手电筒一样扫一遍原本的图片,扫一遍就增加一层。扫了32遍
经过池化层max pooling变成 14 * 14 * 32,在经过第二层的卷积,64个过滤器,变成14 * 14 * 64 在经过一层pooling变成 7 * 7 * 64
扁平序列化变成一个 1 * 1 * 1024在经过一个全连接层的输出
实现如下(逐行注释好了):
# -*- coding: UTF-8 -*-
import tensorflow as tf
# 载入手写数字库[55000 * 28 * 28] 55000训练图像
from tensorflow.examples.tutorials.mnist import input_data
# 存到本地
mnist = input_data.read_data_sets('mnist_data', one_hot=True)
# ont-hot 独热码的编码形式,其实从字面意思很好理解就是,有一位是热的,有一位是取一,其他都取零
# 0,1,2,3,4,5,6,7,8,9 的十位数字
# 0:1000000000 也就是第一位是1,后面同理
# None 表示张量(Tensor)的第一个维度可以是任意长度
# 除以255是为了归一化,把灰度值从[0, 255]变成[0, 1]区间,归一化可以让优化器更快更好的找到误差最小值
input_x = tf.placeholder(tf.float32, [None, 28 * 28]) / 255
output_y = tf.placeholder(tf.int32, [None, 10])
input_images = tf.reshape(input_x, [-1, 28, 28, 1]) # 改变形状
# 从Test(测试)数据集里选取3000个手写数字的图片和对应的标签
test_x = mnist.test.images[: 3000] # 图片
test_y = mnist.test.labels[: 3000] # 标签
# 构建卷积神经网络
# 第一层卷积 input_images => 形状 [ 28 * 28 * 1 ]
# conv2d => 二维的,2 dim
# [28 * 28 * 32]
conv_1 = tf.layers.conv2d(inputs=input_images,
filters=32, # 32个过滤器
kernel_size=[5, 5], # 过滤器大小是5 * 5
strides=1, # 步长是1
padding='same', # same 表示输出大小不变,需要在外围补零
activation=tf.nn.relu
# 激活函数
)
# 第一层池化(亚采样)
# [14 * 14 * 32]
pool_1 = tf.layers.max_pooling2d(
# [28 * 28 * 32]
inputs=conv_1,
# 过滤器 2 * 2
pool_size=[2, 2],
# 步长 2
strides=2
)
# 第二层卷积 pool_1 => 形状 [ 14 * 14 * 32 ]
# [14 * 14 * 64]
conv_2 = tf.layers.conv2d(inputs=pool_1,
filters=64, # 64个过滤器
kernel_size=[5, 5], # 过滤器大小是5 * 5
strides=1, # 步长是1
padding='same', # same 表示输出大小不变,需要在外围补零
activation=tf.nn.relu
# 激活函数
)
# 第二层池化
# [7 * 7 * 64]
pool_2 = tf.layers.max_pooling2d(
# [14 * 14 * 64]
inputs=conv_2,
# 过滤器 2 * 2
pool_size=[2, 2],
# 步长 2
strides=2
)
# 平坦化
flat = tf.reshape(pool_2, [-1, 7 * 7 * 64])
# 1024神经元全连接层
layer_dense = tf.layers.dense(
# [7 * 7 * 64]
inputs=flat,
units=1024,
activation=tf.nn.relu
)
# Dropout : 0.5
dropout = tf.layers.dropout(
inputs=layer_dense,
rate=0.5
)
# 10个神经元的全连接层,不用激活函数做非线性化
logits = tf.layers.dense(
inputs=dropout,
units=10
)
# 计算loss : Cross_entropy(交叉熵)
# 再用softmax计算百分比输出
loss = tf.losses.softmax_cross_entropy(onehot_labels=output_y, logits=logits)
# 用Adam Optimizer 最小化误差, 学习率 0.001
train_op = tf.train.AdamOptimizer(learning_rate=0.001).minimize(loss)
# 计算正确率
accuracy = tf.metrics.accuracy(labels=tf.argmax(output_y, axis=1), predictions=tf.argmax(logits, axis=1))[1]
# 创建会话
sess = tf.Session()
# 初始化全局和局部变量
init = tf.group(tf.global_variables_initializer(), tf.local_variables_initializer())
sess.run(init)
# 我们拿一个epoch来跑一遍 20000 * batch_size(50)
for _ in range(20000):
# 拿下一个batch的信息
batch = mnist.train.next_batch(50)
# run一下loss和优化器, 把之前的两个占位符分别填图片和标签
train_loss, _train_op = sess.run([loss, train_op], {input_x: batch[0], output_y: batch[1]})
# 每一百个batch输出一下
if _ % 100 == 0:
# 测试集上的准确率
# 之前测试集是会取出3000个样本的
test_accuracy = sess.run(accuracy, {input_x: test_x, output_y: test_y})
# 输出训练集损失和测试集准确率
print("%.3f percentage, Train loss = %.3f, (Test accuracy: %.3f)" % (_ / 20000 * 100, train_loss, test_accuracy))
可以观察到训练过程是逐渐收敛的,训练好的模型实际效果就不展示了。
本菜鸟学习不好,如有不妥望各位大佬指点
如要转载请说明原文:https://blog.csdn.net/qq_36652619/article/details/89437256
最后
以上就是爱笑月饼最近收集整理的关于自然语言菜鸟学习笔记(六):CNN(卷积神经网络)理解与实现(TensorFlow)的全部内容,更多相关自然语言菜鸟学习笔记(六)内容请搜索靠谱客的其他文章。








发表评论 取消回复