原文链接(英文):https://databricks.com/blog/2019/02/14/near-real-time-hardware-failure-rate-estimation-with-bayesian-reasoning.html
导语:你可能已经不知不觉中在数据科学项中用上了贝叶斯相关技术!如果你还没用上,这个技术可以增强你的数据分析能力。本文会接着Data Science Central中这篇贝叶斯推理简介文章,展示这项技术在现实世界中的应用案例:通过传感器收集的流式数据预测硬件故障率。如果你对此感兴趣,请继续阅读!
用户案例:硬盘故障
如果你可以检测数据中心的硬盘驱动器,获取包括驱动器型号和故障等信息。你应该想知道哪些硬盘型号的故障率最高。
Backblaze公司收集了近几年内数据中心硬盘运行记录,并公布了它们的故障数据。这些数据按单个驱动器和日期进行细分,并具有来自SMART传感器读数的丰富信息,但本文将仅仅使用驱动器的型号以及它在某一天是否发生故障了的信息。以2018年第二季度和第三季度数据为例,下载CSV文件的压缩包并解压缩到一个共享位置。
最直接的做法是按型号计算故障率,并将其作为实际故障率的最佳估计值。按故障率计算的前六类驱动器是(注意:此处的比例按年度计算为年的故障率,为便于阅读):
from pyspark.sql.functions import *
data_path = ...
agg_df = spark.read.
option("header", True).
option("inferSchema", True).
csv(data_path + "/current/").
select("model", "failure").
groupBy("model").
agg({"*": "count", "failure": "avg"}).
filter("avg(failure) > 0").
orderBy(desc("avg(failure)")).
limit(6).
cache()
display(agg_df.withColumn("pct_failure", col("avg(failure)") * 100.0))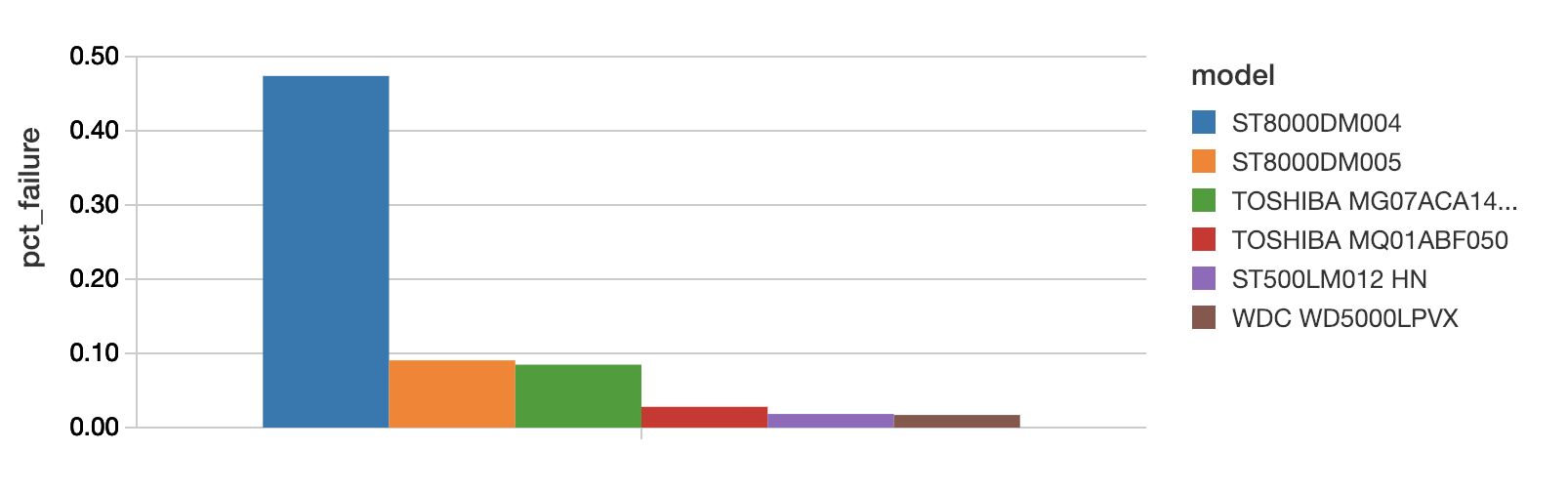
(在Databricks平台,只需使用单元格输出中的绘图选项就可以将结果的表格视图切换到上面的直方图。) 型号 ST8000DM004 全年故障率是0.5%,看起来是一个很高的数值,但是,我们也无法确定它是否只是在第二季度和第三季度经历了高故障率而已。
假设有一个真实的故障率 λ,那么单位时间内的故障数目应遵循泊松分布Poisson(λ)(就像抛硬币实验中正面朝上的次数遵循二项分布)。 如上所述,我们希望能理解故障率λ本身的概率分布,它遵循一个带两个参数ɑ和β的伽马分布(gamma distribution)。和贝塔分布(Beta distribution)一样,他们有一个简答的解释:在t天内观察到f次故障后,故障率λ的分布是Gamma(f,t)。
import numpy as np
import scipy.stats as stats
from pyspark.sql.types import *
to_gamma_schema = ArrayType(StructType([StructField("rates", DoubleType()), StructField("pdfs", DoubleType())]))
def build_gamma_udf(df, max_scale_factor=1):
max_avg_failure = df.select(max("avg(failure)")).collect()[0][0]
# Computes the PDF of the gamma distribution at points for each model's rate param
def to_gamma_pdf(count, avgf):
# k = alpha = number of failures
k = count * avgf
# theta = 1/beta, where beta = total observations
theta = 1.0 / count
# Pick rates to try with more samples at small rates
rates = np.geomspace(max_avg_failure / 1000, max_avg_failure * max_scale_factor, 100)
# Calculate the probability distribution function at those points
pdfs = stats.gamma.pdf(rates, a=k, scale=theta)
return list(zip(rates.tolist(), pdfs.tolist()))
return udf(to_gamma_pdf, to_gamma_schema)
to_gamma_pdf_udf = build_gamma_udf(agg_df)
gamma_df = agg_df.
withColumn("rates_pdfs", explode(to_gamma_pdf_udf("count(1)", "avg(failure)"))).
select("model", col("rates_pdfs.rates").alias("rate"), col("rates_pdfs.pdfs").alias("pdf"))
display(gamma_df.withColumn("pct_rate", col("rate") * 100.0))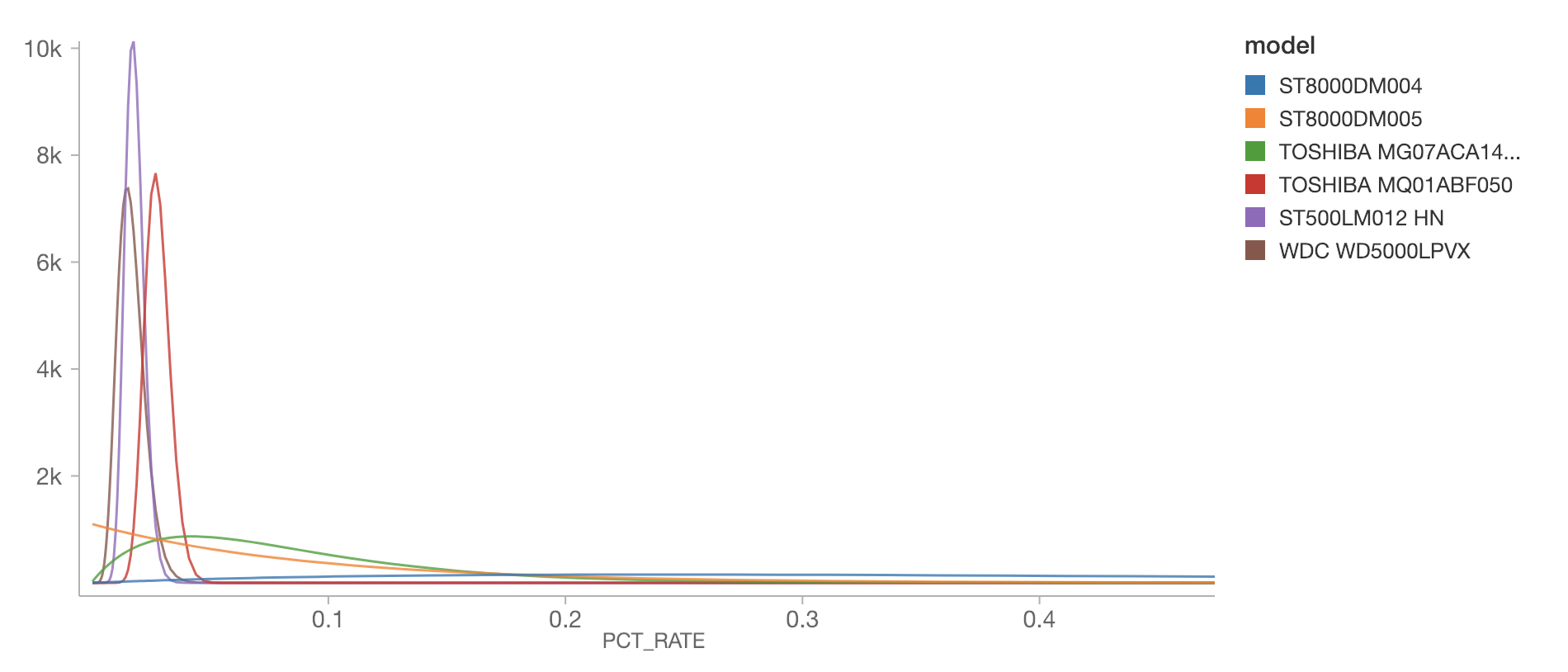
我们注意到不同型号硬盘的预估故障率分布是非常不一样的。型号ST8000DM004有着非常广的概率分布,同时,不得不承认它也有着更高的故障率;为了显示方便我们只截取了部分曲线,但它的很大一部分概率分布在大于每年0.4%的区间。这是因为相对而言这个型号硬盘的观察样本比较少,见下表: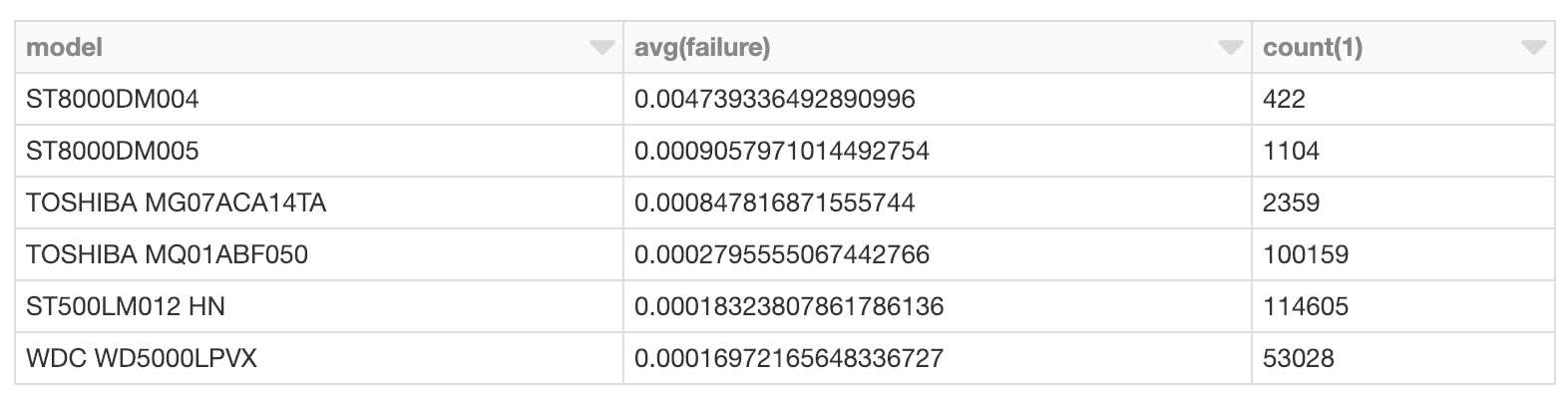
放大左侧的两个峰值分布,分别是“ST500LM012 HN”和“WDC WD5000LPVX”: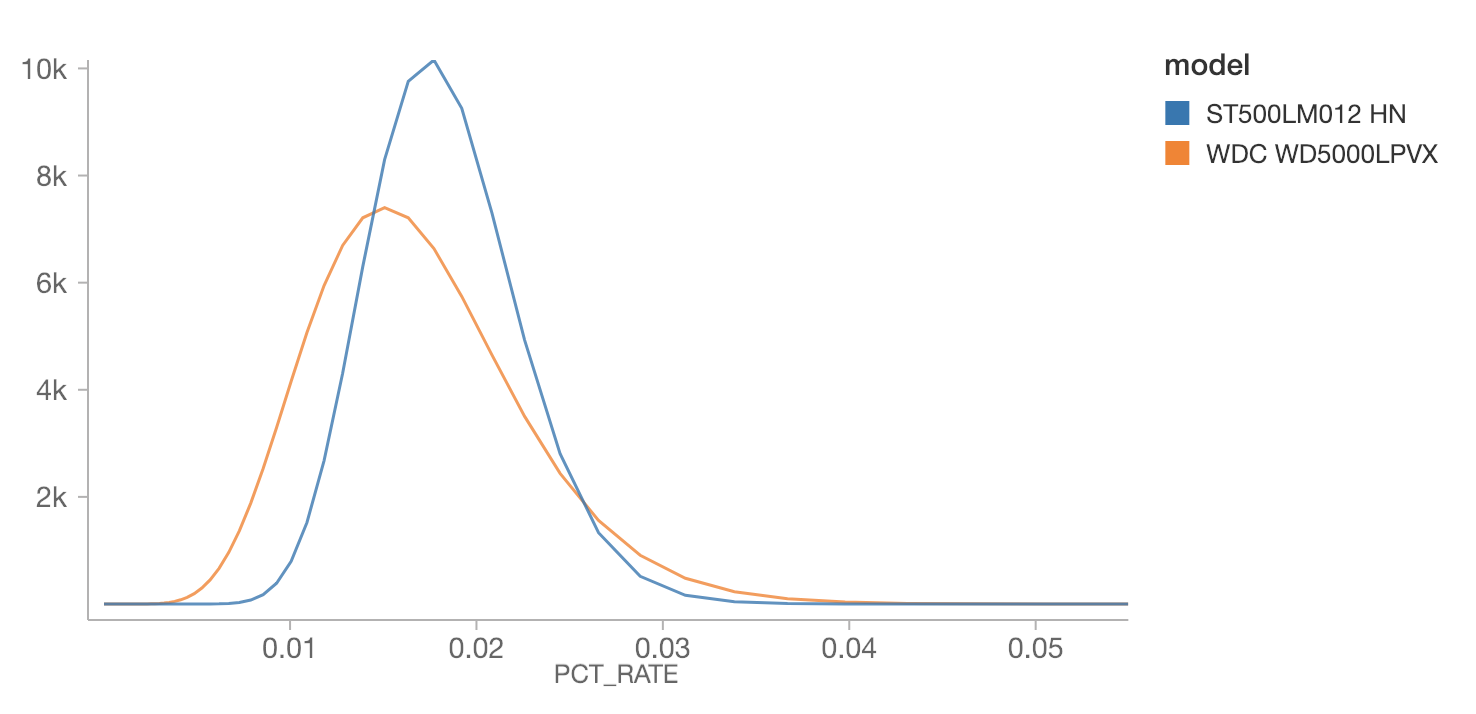
有趣的是,WDC可能性最高的年故障率是比ST500低的(大概是0.015% 比 0.02%)。但是,因为WDC的观测样本较少,所以它的可能故障率分布会更广。如果我们的问题是哪种型号的故障率最有可能高于0.03%,基于当前的信息,WDC反而是更有可能的。类似的场景比如说:我们需要决定哪个型号的故障最有可能超出制造商的可容忍上限。此时,不仅仅是最大后验概率估计,概率分布也同样重要。
用先验概率分析数据流中的故障信息
实际上,这些观测数据并非一次性全部能获取到。数据是以流的形式到达,所以很自然的我们需要持续的运行这些计算程序。 Apache Spark Structured Streaming非常适合用来处理这种数据,它可以几乎完全相同的形式运行上述代码。
当然,这类流式分析程序从第一天就开始运行时,并没有任何历史数据。甚至当积累了两个季度的数据之后,故障的案例相对而言还是太少,所以故障率的不确定性还非常高。
当一个组织或公司向把离线数据架构转换为在线流式处理模式,他们应该已经积累的不少历史数据。这只是关于故障率的先验信念,可以作为故障率的先验分布注入。
伽马分布可以方便的和泊松分布共轭(conjugate),所以我们可以使用伽马分布去代表先验概率,并且在观测到一些数据之后,可以很简答的计算得到后验伽马分布(不需要使用很复杂的数学计算)。因为伽马分布的 ɑ 和 β 两个参数可以分别被解释为故障数目和运行天数,所以这些值可以通过历史数据计算出来,并通过Spark Structured Streaming作业持续的计算和更新。请看示例:
priors_df = spark.read.
option("header", True).
option("inferSchema", True).
csv(data_path + "/historical/").
select("model", "failure").
groupBy("model").
agg({"*": "count", "failure": "avg"}).
withColumn("alpha", col("count(1)") * col("avg(failure)")).
withColumn("beta", col("count(1)")).
select("model", "alpha", "beta").
cache()
agg_stream = spark.readStream.
schema(raw_df.schema).
option("header", True).
option("maxFilesPerTrigger", 1).
csv(data_path + "/current/").
select("model", "failure").
groupBy("model").
agg({"*": "count", "failure": "avg"}).
filter("avg(failure) > 0").
orderBy(desc("avg(failure)")).
limit(6)
max_avg_failure = priors_df.select(avg(col("alpha") /
col("beta")).alias("failure_rate")).agg(max("failure_rate")).collect()[0][0]
def to_gamma_pdf(count, avgf, prior_alpha, prior_beta):
# Note: priors are added below
k = prior_alpha + count * avgf
theta = 1.0 / (prior_beta + count)
rates = np.geomspace(max_avg_failure / 1000, max_avg_failure, 100)
pdfs = stats.gamma.pdf(rates, a=k, scale=theta)
return list(zip(rates.tolist(), pdfs.tolist()))
to_gamma_pdf_udf = udf(to_gamma_pdf, to_gamma_schema)
gamma_stream = agg_stream.
join(priors_df, "model", how='left').
fillna(0, subset=["alpha", "beta"]).
withColumn("gamma", to_gamma_pdf_udf("count(1)", "avg(failure)", "alpha", "beta")).
select("model", explode("gamma").alias("rates_pdfs")).
select("model", col("rates_pdfs.rates").alias("rate"), col("rates_pdfs.pdfs").alias("pdf"))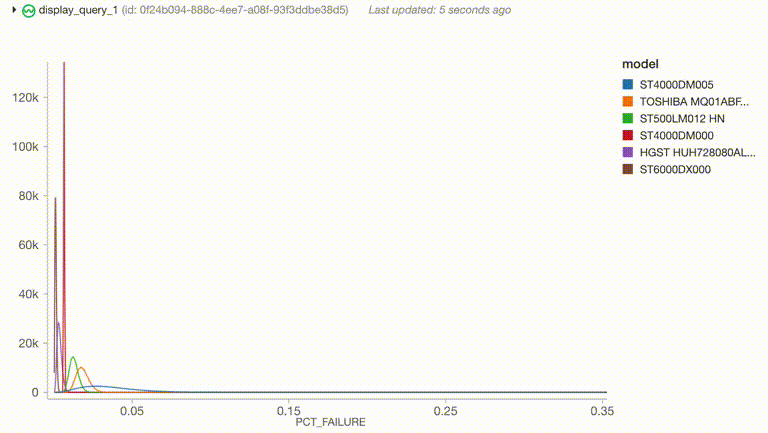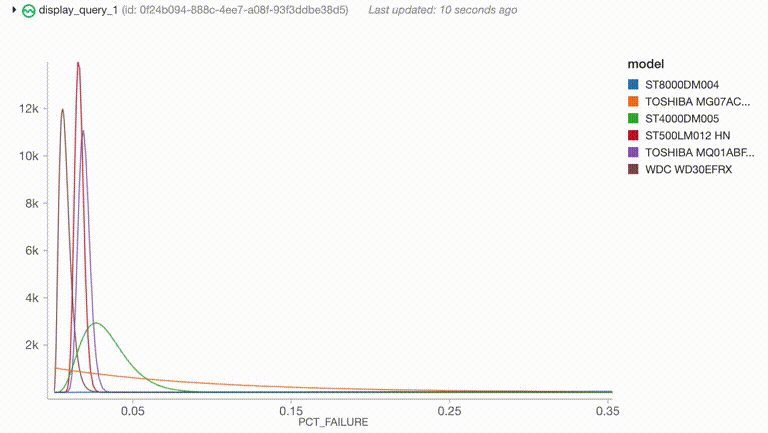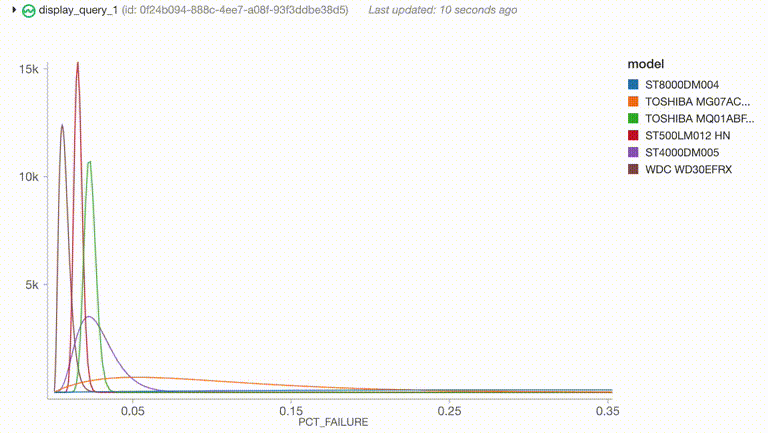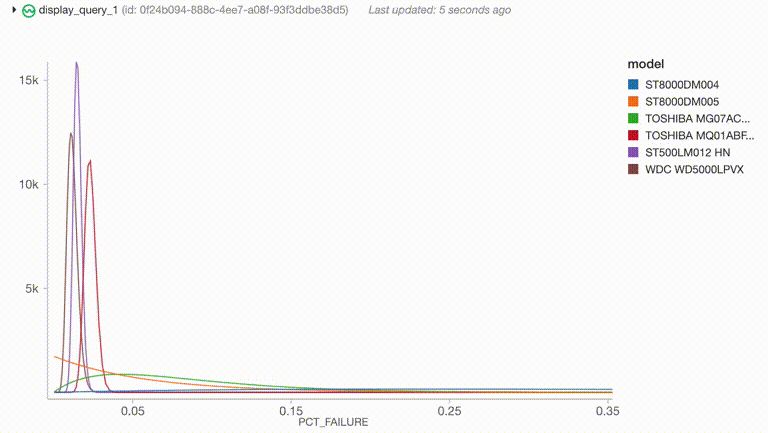
通过历史数据计算产生了各个硬盘型号先验分布的ɑ和β参数,然后可以很方便的和流式数据进行Join(这里的流式数据是我们模拟得到的)
开始运行之后,程序生成了一个不断更新的图表来展示当前最高故障率的硬盘型号的故障率分布情况。它可以很容易地生成报警,或者根据概率分布的其他功能生成其他警报,并且可以使用几乎相同的代码生成简单的离线分析程序。
结语
当你在拟合一个分布曲线时,实际上发生的事情比你想象的更多。你可能已经在不知不觉中使用了“概率派”或“贝叶斯派”的推理方法。贝叶斯派观点有一些优点,因为在寻找答案过程中考虑了先验知识,并产生的是答案的一个概率分布而不只是一个估计值。通过Spark的Structured Streaming技术以及对先验和后验分布的理解,可以将贝叶斯方法论方便的应用到现实世界的实践中。
最后
以上就是辛勤纸鹤最近收集整理的关于 [译]利用贝叶斯推理做硬件故障率的准实时预测 的全部内容,更多相关 内容请搜索靠谱客的其他文章。




![[译]利用贝叶斯推理做硬件故障率的准实时预测](https://www.shuijiaxian.com/files_image/reation/bcimg11.png)



发表评论 取消回复