在Unity3D当中有一个FingerGesture的插件,这个插件可以让你在普通的屏幕上以鼠标模拟手机触摸屏的Touch事件,从而方便调试,另外,这个插件还可以帮忙让Unity项目在红外边框触摸屏下正常的发挥触摸作用。关于这款插件的使用,我这边先不多说,下面主要说一下的是这个插件当中的一个有趣的功能——自定义手势识别所用到的算法。
这个算法就是:$P Point-Cloud Recognizer
它是由Radu-Daniel Vatavu ,Lisa Anthony 还有 Jacob O. Wobbrock 三人共同发布的一个算法,之前他们还发布了$1(单笔画手势识别) $N(多笔画手势识别)等实用算法,但是它们各自都有着自己的缺陷。而$P(点云识别算法)的出现正是给这些算法的缺陷进行填补,它同时兼备了多笔画和单笔画的识别功能,还解决了$N当中会出现的由于存储手势的排列组合而造成的内存占用过高的问题(因为$P不用记录笔画的顺序和多少)。
我们可以先简单了解一下该算法大概内容描述:
关于手势识别,我们可以理解成是关于两个点对集之间的匹配问题,通过将待匹配手势和手势模板这两个点对集转换放于同一个坐标体系下,然后求相对点之间的欧氏距离加和得到最小的值,则可以认为是所匹配的手势。例如:有一个待确认手势点对集C 和 一个候选手势模板T,对于每一个点 Ci 均有相应的对应点 Tj , 那么,这两个点对集之间的欧氏距离和为:
我们将手势C和手势模板里面的各个备选手势T进行欧氏距离的计算,当出现最小的值的时候,我们认为当前的T是最匹配C的存在。(实际上这要匹配出n! 种可能性)
其实上面的问题可以转化为一个大家都很熟悉的问题:分配问题。
有n个问题要分配给n个人去完成。第i个人完成第j项任务的成本为Cij。问:如何分配任务,能使总成本最小?
这个问题由匈牙利算法可以很好的解决,同时在算法创造者的验证下,匈牙利算法也是进行手势匹配最精确的算法,但是无奈的是它的时间复杂度较高,执行时间代价太大。所以作者推出了新的识别方案,从另一个角度来看,我觉得它可以称为伪·匈牙利算法了 : ) 。
因为选取的起点不一样的情况下,匹配到的结果就会不尽相同,所以$P在匹配的过程当中是进行了随机的选取起始点,多组求欧氏距离,从而在其中选择最优方案,修正过后的公式应该是下面这样的:
但是我们知道,当第 i 点匹配的时候, i+1个点可以选择的匹配范围就会变少,也就是说,进行匹配的点之间是有一定的权重的,第一个点的权重是最大的,他的可信度是最高,因为他所匹配的是整个点集之间选取,而最后一个点是最不可信的,因为它只能选择剩下的点,所以在算法的基础上,作者们加上了一个权重加衡:
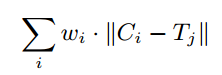
至此,$P的核心数学模型已经成型了。关于更详细的验证和解释,请有兴趣的读者自行翻阅算法创造者的论文:http://faculty.washington.edu/wobbrock/pubs/icmi-12.pdf
下面是该算法的伪代码实现过程(同时附上链接:http://depts.washington.edu/aimgroup/proj/dollar/pdollar.pdf):
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Recognizer main function. Match points against a set of templates by employing the Nearest-Neighbor classification rule.Returns a normalized score in [0..1] with 1 denoting perfect match.
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
$P-Recognizer (Points points, Templates templates) // 核心识别
1: n ← 32 // number of points
2: Normalize(points, n)
3: score ← ∞
4: for each template in templates do
5: Normalize(template, n) // should be pre-processed
6: d ← Greedy-Cloud-Match(points, template, n)
7: if score > d then
8: score ← d
9: result ← template
10: score ← Max((2.0−score)/2.0, 0.0) // normalize score in [0..1]
11: return result, score
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Cloud matching function. Match two clouds (points and template) by performing repeated alignments between their points(each new alignment starts with a different starting point index i).Parameter ∈ [0..1] controls the number of tested alignments(n ∈ {1,2, ...n}). Returns the minimum alignment cost.
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Greedy-Cloud-Match (Points points, Points template, int n)1: e←0 .50
2: step ← n^(1-e)
3: min ← ∞
4: for i = 0 to n step step do
5: d1 ← Cloud-Distance(points, template, n, i)
6: d2 ← Cloud-Distance(template, points, n, i)
7: min ← Min(min, d1, d2)
8: return min
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Distance between two clouds. Compute the minimum-cost alignment between points and tmpl starting with point start.
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Cloud-Distance (Points points, Points tmpl, int n, int start)
1: matched ← new bool[n]
2: sum ← 0
3: i ← start // start matching with pointsi
4: do
5: min ← ∞
6: for each j such that not matched[j] do
7: d ← Euclidean-Distance(pointsi, tmplj)
8: if d < min then
9: min ← d
10: index ← j
11: matched[index] ← true
12: weight ← 1 − ((i − start + n) MOD n)/n
13: sum ← sum + weight · min
14: i ← (i + 1) MOD n
15: until i == start // all points are processed
16: return sum
上面就是$P的核心算法实现了,下面贴出来的,则是调用算法前所做的一些工作:将手势的点进行序列化,和模板转换成在统一坐标系,求亮点间的欧氏距离啊等等
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Gesture normalization. Gesture points are resampled, scaled with shape preservation, and translated to origin.
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
1: points ← Resample(points, n)
2: Scale(points)
3: Translate-to-Origin(points, n)
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Points resampling. Resample a points path into n evenly spaced points. We use n = 32.(文章中提到,重采样n的值越大,越精确,同时耗时越多)
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
2: D ← 0
3: newP oints ← points0
4: for each pi in points such that i ≥ 1 do
5: if pi.strokeId == pi−1.strokeId then
6: d ← Euclidean-Distance(pi−1, pi)
7: if (D + d) ≥ I then
8: q.x ← pi−1.x +((I − D)/d) · (pi.x - pi−1.x)
9: q.y ← pi−1.y +((I − D)/d) · (pi.y - pi−1.y)
10: q.strokeId ← pi.strokeId
11: Append(newP oints, q)
12: Insert(points, i, q) // q will be the next pi
13: D ← 0
14: else D ← D + d
15: return new Points
1: d ← 0
2: for each pi in points such that i ≥ 1 do
3: if pi.strokeId == pi−1.strokeId then
4: d ← d + Euclidean-Distance(pi−1, pi)
5: return d
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Points rescale. Rescale points with shape preservation so that the resulting bounding box will be ⊆ [0..1] × [0..1].
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
1: xmin ← ∞, xmax ← 0, ymin ← ∞, ymax ← 0
2: for each p in points do
3: xmin ← Min(xmin, p.x)
4: ymin ← Min(ymin, p.y)
5: xmax ← Max(xmax, p.x)
6: ymax ← Max(ymax, p.y)
7: scale ← Max(xmax − xmin, ymax − ymin)
8: for each p in points do
9: p ← ((p.x −xmin)/scale, (p.y −ymin)/scale, p.strokeId)
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
1: c ← (0,0) // will contain centroid
2: for each p in points do
3: c ← (c.x + p.x, c.y + p.y)
4: c ← (c.x/n, c.y/n)
5: for each p in points do
6: p ← (p.x - c.x, p.y - c.y, p.strokeId)
最后
以上就是野性裙子最近收集整理的关于关于$P Point-Cloud Recognizer (点云手势识别)的理解的全部内容,更多相关关于$P内容请搜索靠谱客的其他文章。

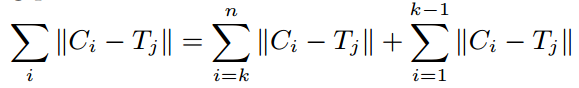



![[论文阅读:姿态识别&Transformer] TFPose: Direct Human Pose Estimation with Transformers[论文阅读:姿态识别&Transformer] TFPose: Direct Human Pose Estimation with Transformers](https://www.shuijiaxian.com/files_image/reation/bcimg1.png)





发表评论 取消回复