! 单位荷载作用下结果稳态分析apdl流程
load_point=6719
view_point=6843
load_f=-100
! 完全法
/solu
time,1
allsel,all
antype,0 ! 0 Static 1 buckel 2 modal 3 harmic 4 trans 7 substr 8 specterx
! autots,on !自动时间步
OUTRES,all,all !全输出
!nlgeom,off !几何非线性因素
!nropt,full !牛顿拉普森处理 full完全方式 modl 修正方式
allsel
F,load_point,fz,load_f ! 施加载荷 F, NODE, Lab, VALUE, VALUE2, NEND, NINC
nsubst,50
allsel
SOLVE
time,2
F,load_point,fz,100
nsubst,50
SOLVE
FINISH
按照上述采用连续求解,荷载步变化如图

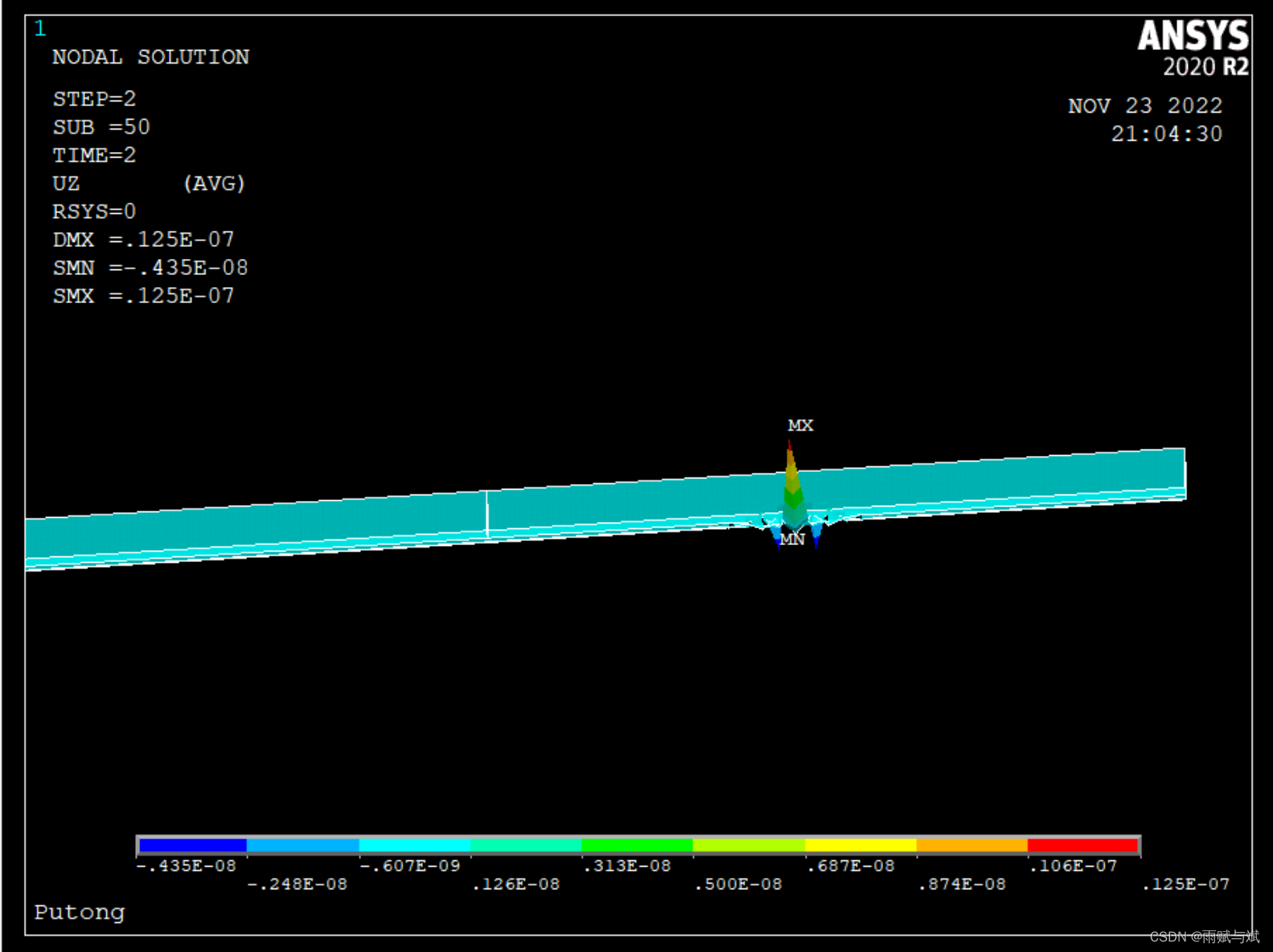
在第1荷载步50子步时,如图所示
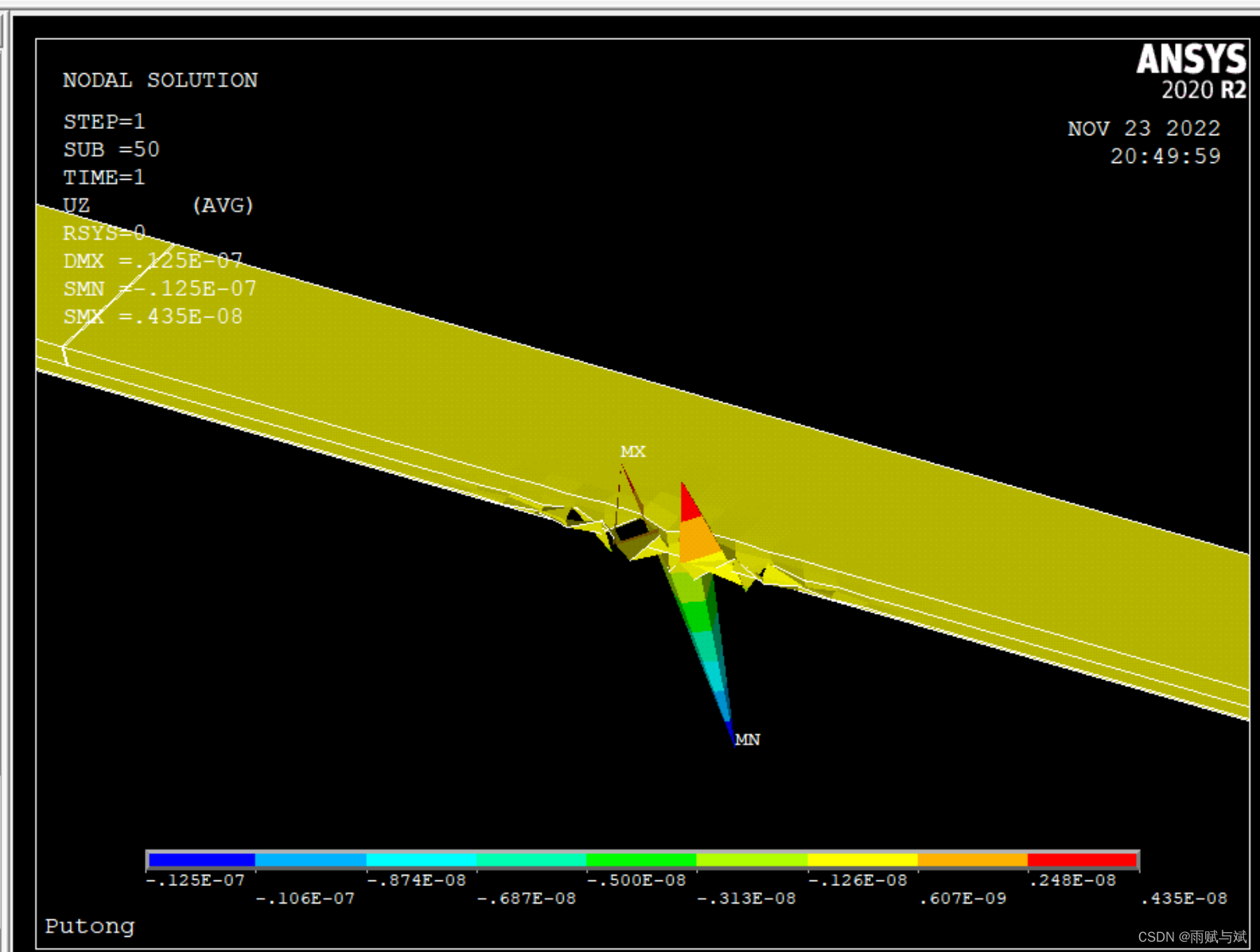
在第2荷载步24子步时,如图所示

在第2荷载步25子步时,如图所示
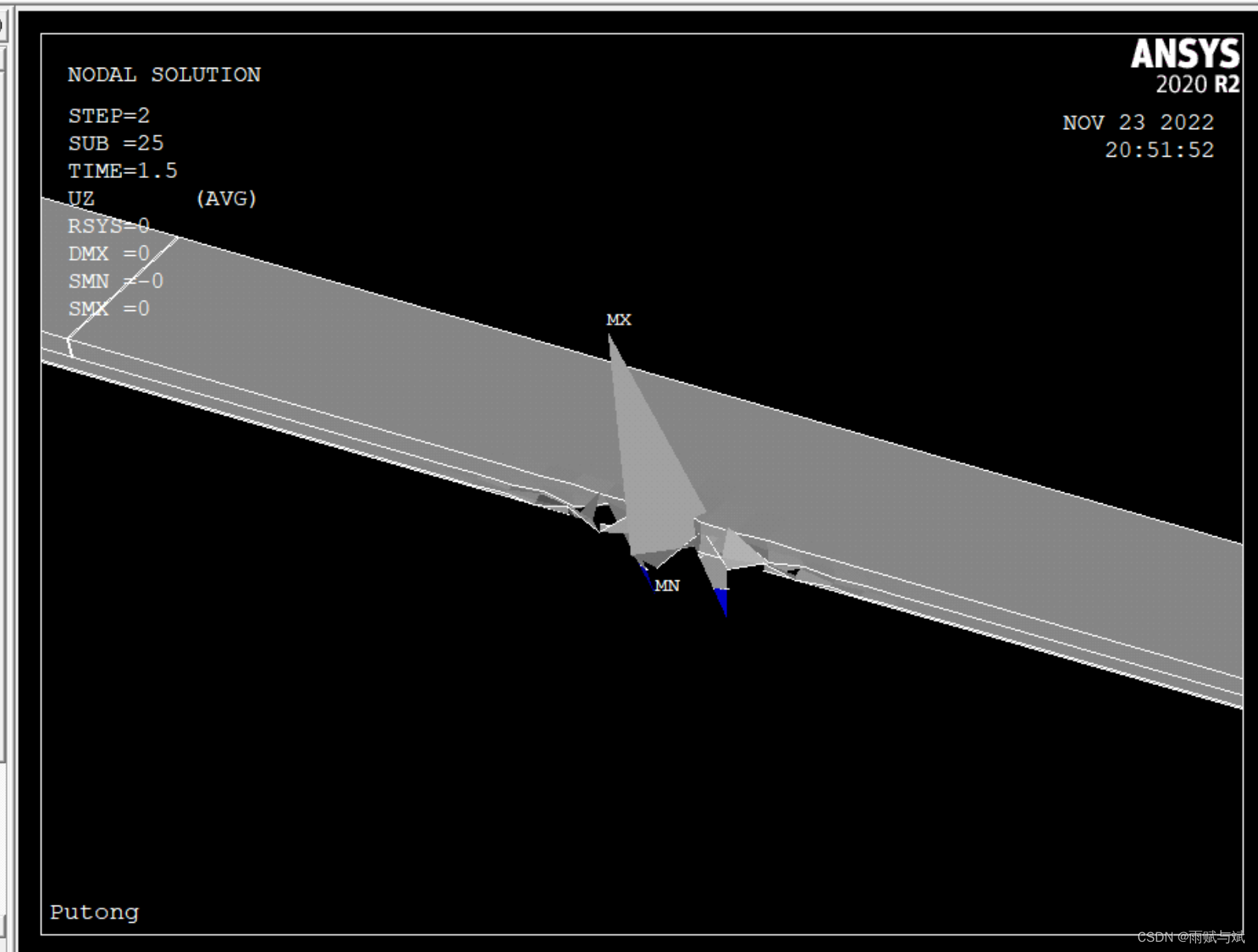
在第2荷载步26子步时,如图所示
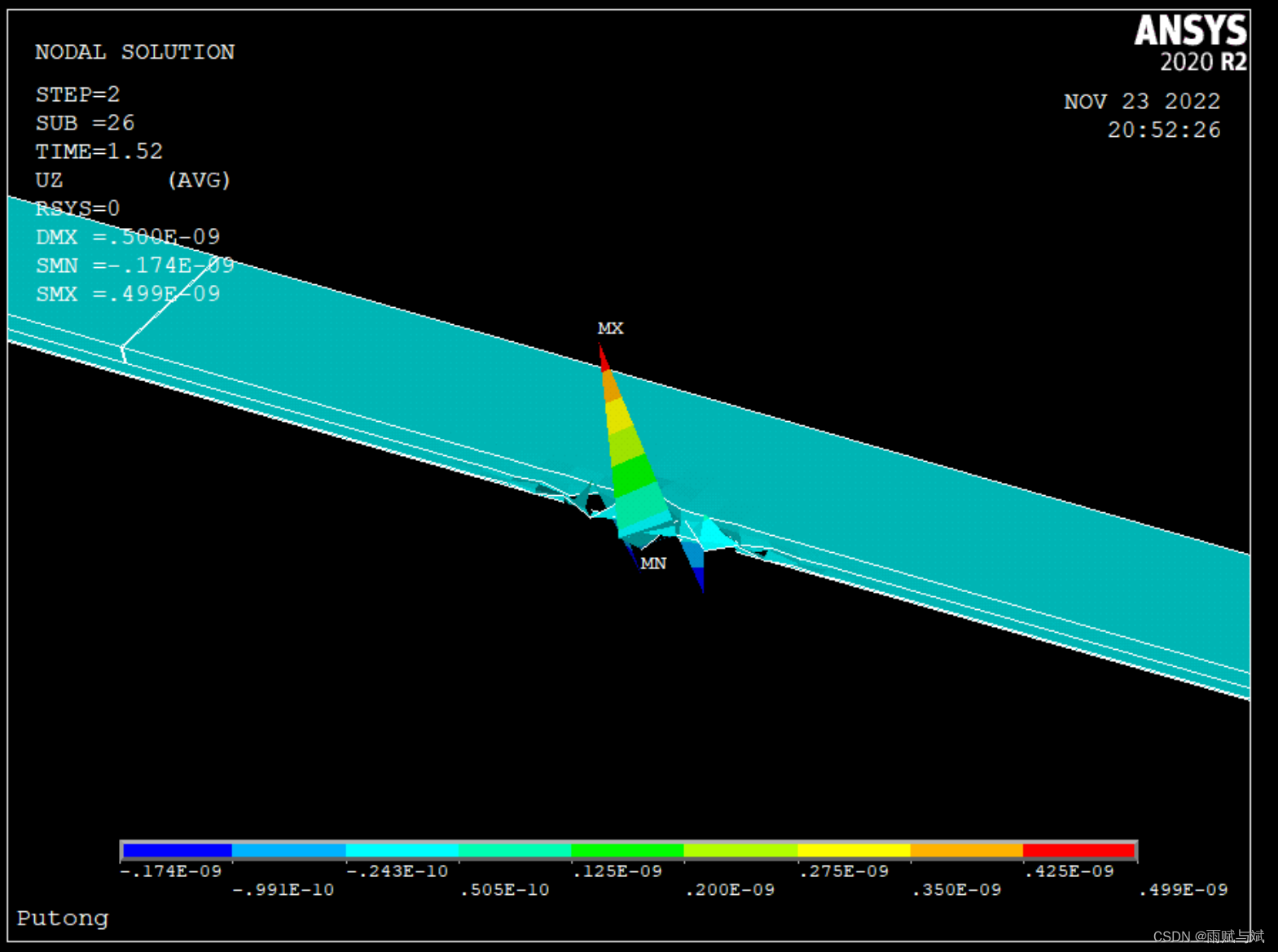
在第2荷载步50子步时,如图所示
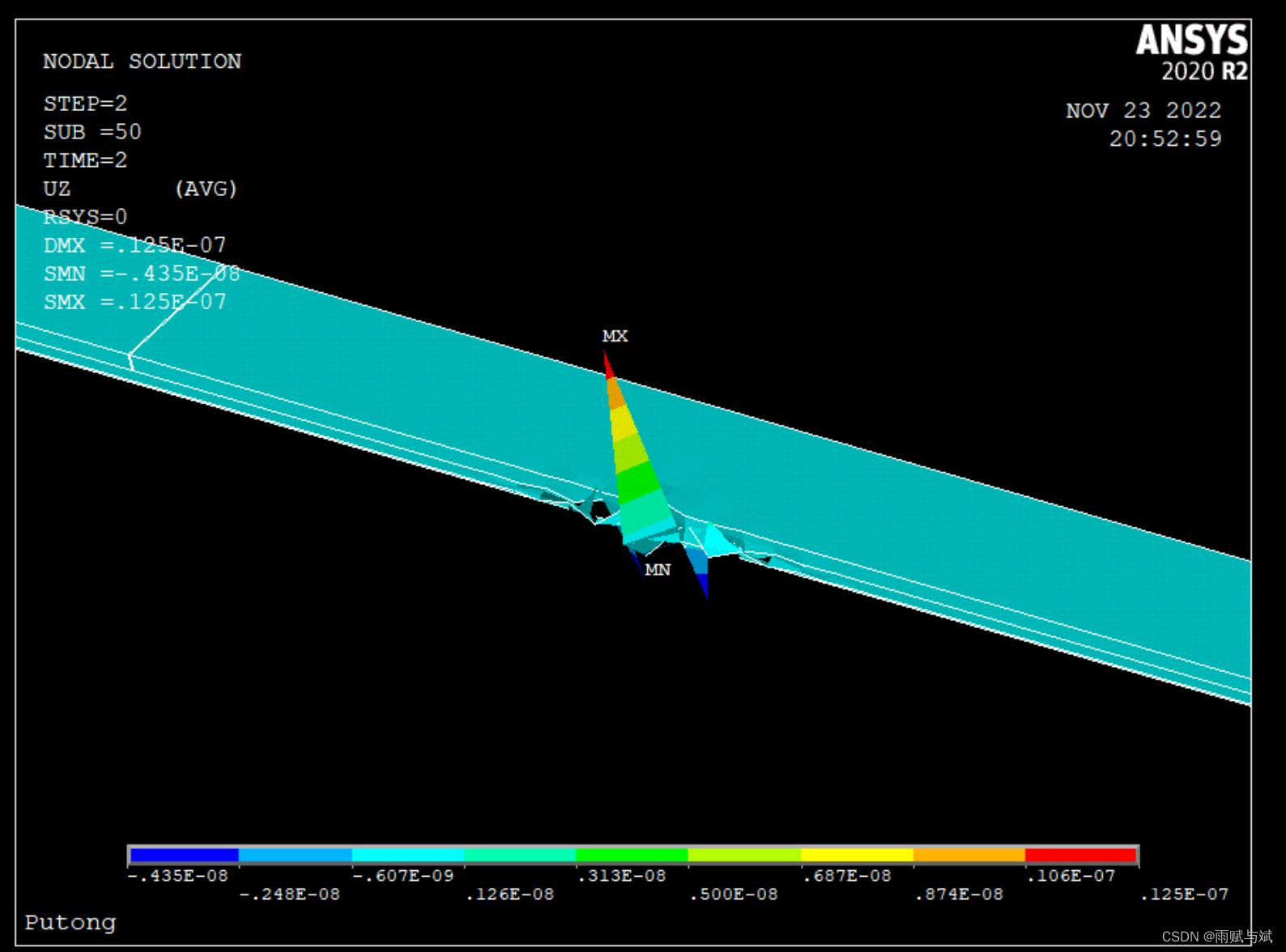
发现当图一中荷载为0时,图中没有弯矩,在第1的1和第2的25处最大值最小值相反,说明力的加载是按图1的线性变化加载的
当加入kbc=1,荷载阶跃后,荷载变化图如图
命令流如下
load_point=6719
view_point=6843
load_f=-100
! 完全法
/solu
time,1
allsel,all
antype,0 ! 0 Static 1 buckel 2 modal 3 harmic 4 trans 7 substr 8 specterx
! autots,on !自动时间步
OUTRES,all,all !全输出
!nlgeom,off !几何非线性因素
!nropt,full !牛顿拉普森处理 full完全方式 modl 修正方式
KBC,1
allsel
F,load_point,fz,load_f ! 施加载荷 F, NODE, Lab, VALUE, VALUE2, NEND, NINCnsubst,50
allsel
SOLVEtime,2
F,load_point,fz,100
nsubst,50
KBC,1
SOLVE
FINISH
第1荷载步的第1子步,第50子步,第2荷载步的第1子步,第50子步如图



说明阶跃是从第一子步开始的
当调换加载time,和f的相对位置后
代码
load_point=6719
view_point=6843
load_f=-100
! 完全法
/soluallsel,all
antype,0 ! 0 Static 1 buckel 2 modal 3 harmic 4 trans 7 substr 8 specterx
! autots,on !自动时间步
OUTRES,all,all !全输出
!nlgeom,off !几何非线性因素
!nropt,full !牛顿拉普森处理 full完全方式 modl 修正方式
! KBC,1
allsel
F,load_point,fz,load_f ! 施加载荷 F, NODE, Lab, VALUE, VALUE2, NEND, NINCnsubst,50
allsel
time,1
SOLVE
F,load_point,fz,100
nsubst,50
! KBC,1
time,2
SOLVE
FINISH
结果如下

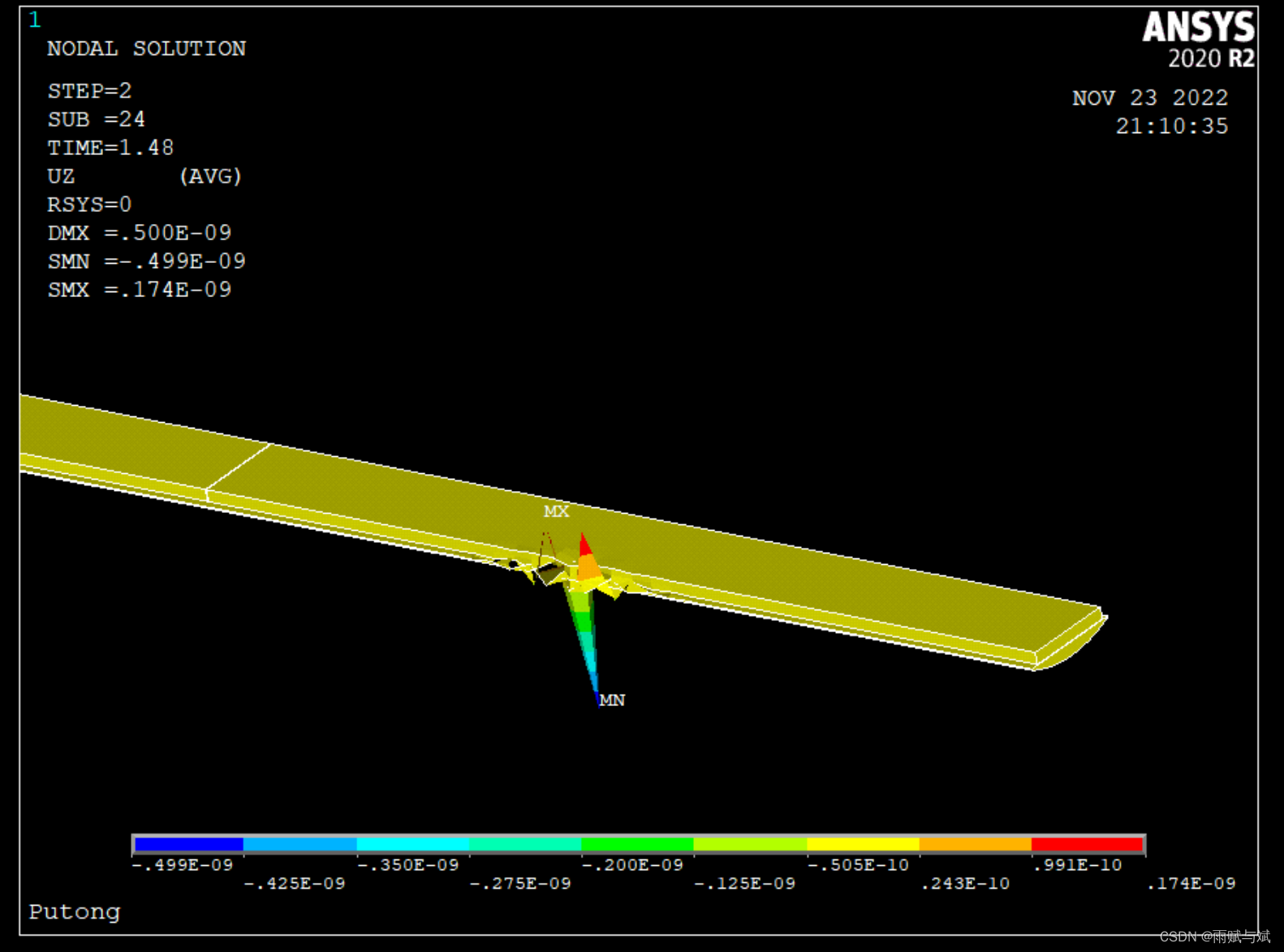

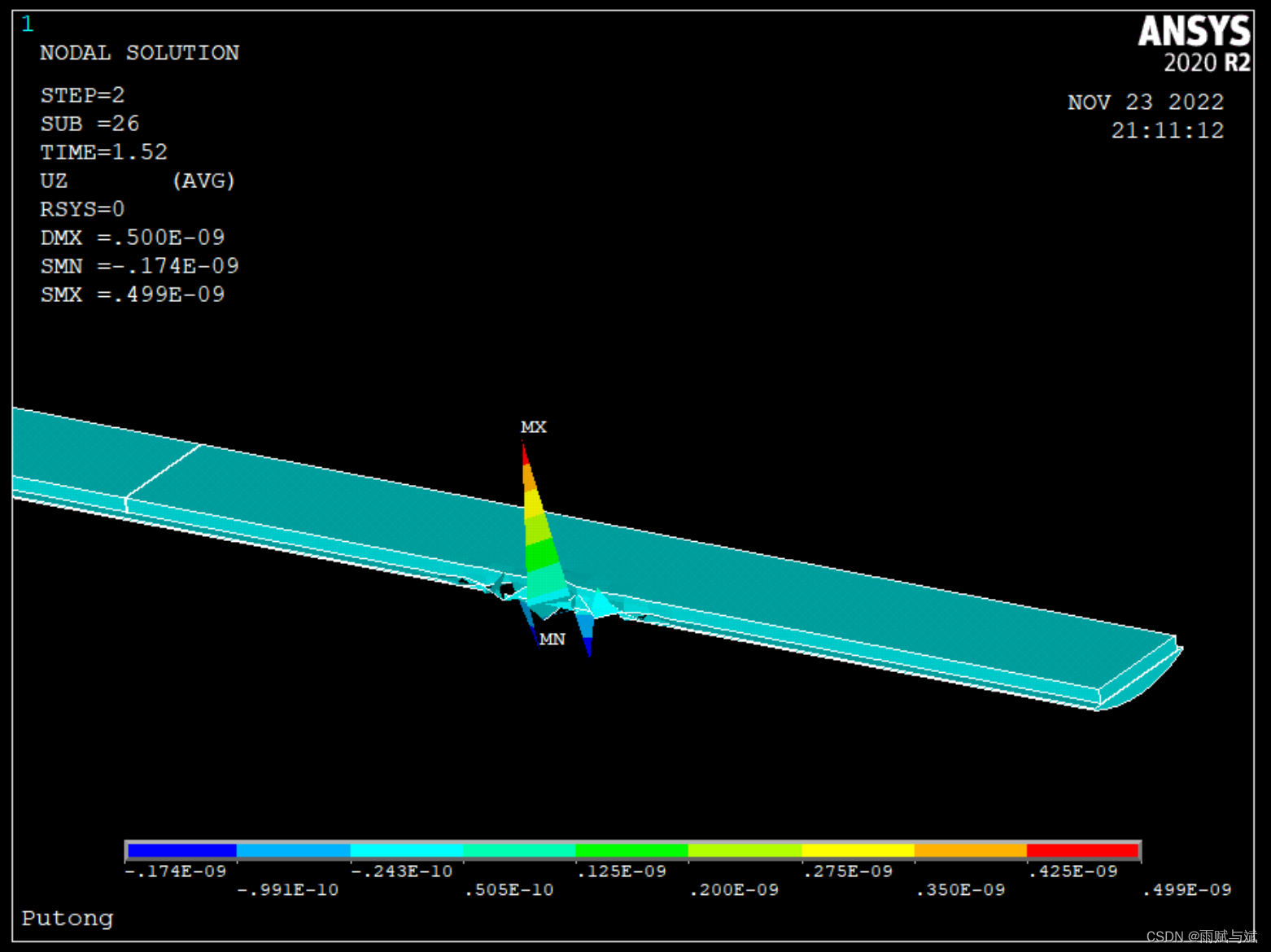
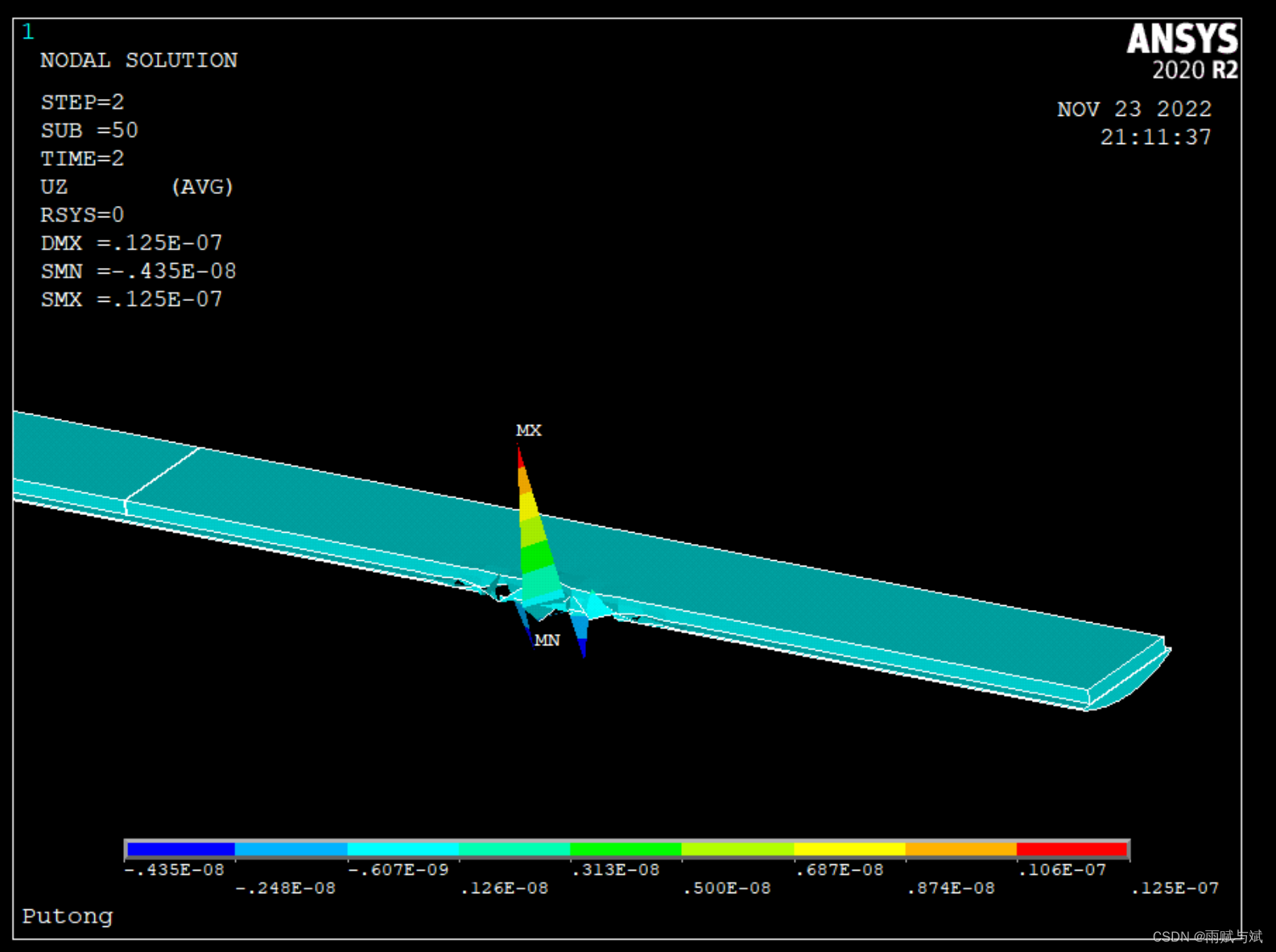
这说明time=1和f的相对位置不会影响计算结果,共同设置一个荷载步端点的时间的力的大小
但每次计算完若进入了post1查看结果,则再次进入solu后计算会覆盖原先的结果,因此连续求解过程不能被打断,
看利用lswrite荷载步文件
! 写入荷载步文件求解
load_point=6719
view_point=6843
load_f=-100
! 完全法
/solu
time,1
allsel,all
antype,0 ! 0 Static 1 buckel 2 modal 3 harmic 4 trans 7 substr 8 specterx
! autots,on !自动时间步
OUTRES,all,all !全输出
!nlgeom,off !几何非线性因素
!nropt,full !牛顿拉普森处理 full完全方式 modl 修正方式
! KBC,1
allsel
F,load_point,fz,load_f ! 施加载荷 F, NODE, Lab, VALUE, VALUE2, NEND, NINC
nsubst,50
allsel
lswrite,1
time,2
F,load_point,fz,100
nsubst,50
! KBC,1
lswrite,2
F,load_point,fz,0
nsubst,50
! KBC,1
time,3
lswrite,3
lssolve,1,2
FINISH
其结果与连续求解一致
说明lswrite不删除原来的荷载,其荷载步图也为下图

如果载荷呈递增或阶跃式变化,为了提高计算精度。
1、可以通过nsubst设置载荷子步以及kbc设置载荷递增方式。
ANSYS中谐响应分析的载荷(力和位移等)有两种输入形式,分别是幅值、相位形式和实部、虚部形式,二者是等价的。实际分析问题时,采取何种形式的输入,取决于哪种输入形式更方便。
1. 振幅和相角
(1)载荷值(大小)代表振幅 Fmax
(2)相角 f 是在两个或两个以上谐波载荷间的相位差,单一载荷不需要相角 f 。
(3)ANSYS 不能直接输入振幅和相角,而是规定实部和虚部分量;
例如,施加两个简谐力 F1和 F2 ,其相角相差 f:
F1real = F1max (F1的振幅)F1imag = 0
F2real = F2maxcosfF2imag = F2maxsinf
(4)可以使用APDL语言计算,但要确保角度单位为度(缺省为弧度)。
参考(36条消息) ansys谐响应分析_pingmin2014的博客-CSDN博客_ansys 谐响应分析
finish
/clear
/prep7
kk=1000
mm=10
c=10
p0=40
et,1,combin14,,,2
et,2,mass21,,,4
r,1,kk,c
r,2,mm
n,1
n,2,1$type,1
real,1
e,1,2
type,2
real,2
e,2
d,1,all
d,all,uy
kes=c/(2*sqrt(kk*mm))
peakf=sqrt(1-2*kes*kes)*sqrt(kk/mm)/2/acos(-1)
/solu
ANTYPE,HARMIC
!设定分析类型为谐响应分析
HROPT,Full
!求解方法为完全法
HROUT,on
!指定谐波分析输出选项,Reimky(实部虚部),Clust(固有频率群频解),Mcont(模态贡献量)
KBC,1
! 0 从上一加载步到本加载步载荷线性变换, 1 荷载阶跃式突变
NSUBST,50
! 子步数,即在频率范围内细分多少个频率点,决定频率分辨率
HARFRQ,0,2*peakf
! 频率范围
*do,i,1,10
faii=10*(i-1)/180*acos(-1)
fi=10*i
fir=fi*cos(faii)
fii=fi*sin(faii)
f,2,fx,fir,fii
solve
*enddo
/post26
nsol,2,2,u,x
plcplx,0!设置复数变量的显示方式,
plvar,2plcplx,0!设置复数变量的显示方式,0为幅值,1为相位角,2为实部,3为虚部
10条幅频曲线对应10个简谐荷载

plcplx,1!设置复数变量的显示方式,0为幅值,1为相位角,2为实部,3为虚部
plvar,2
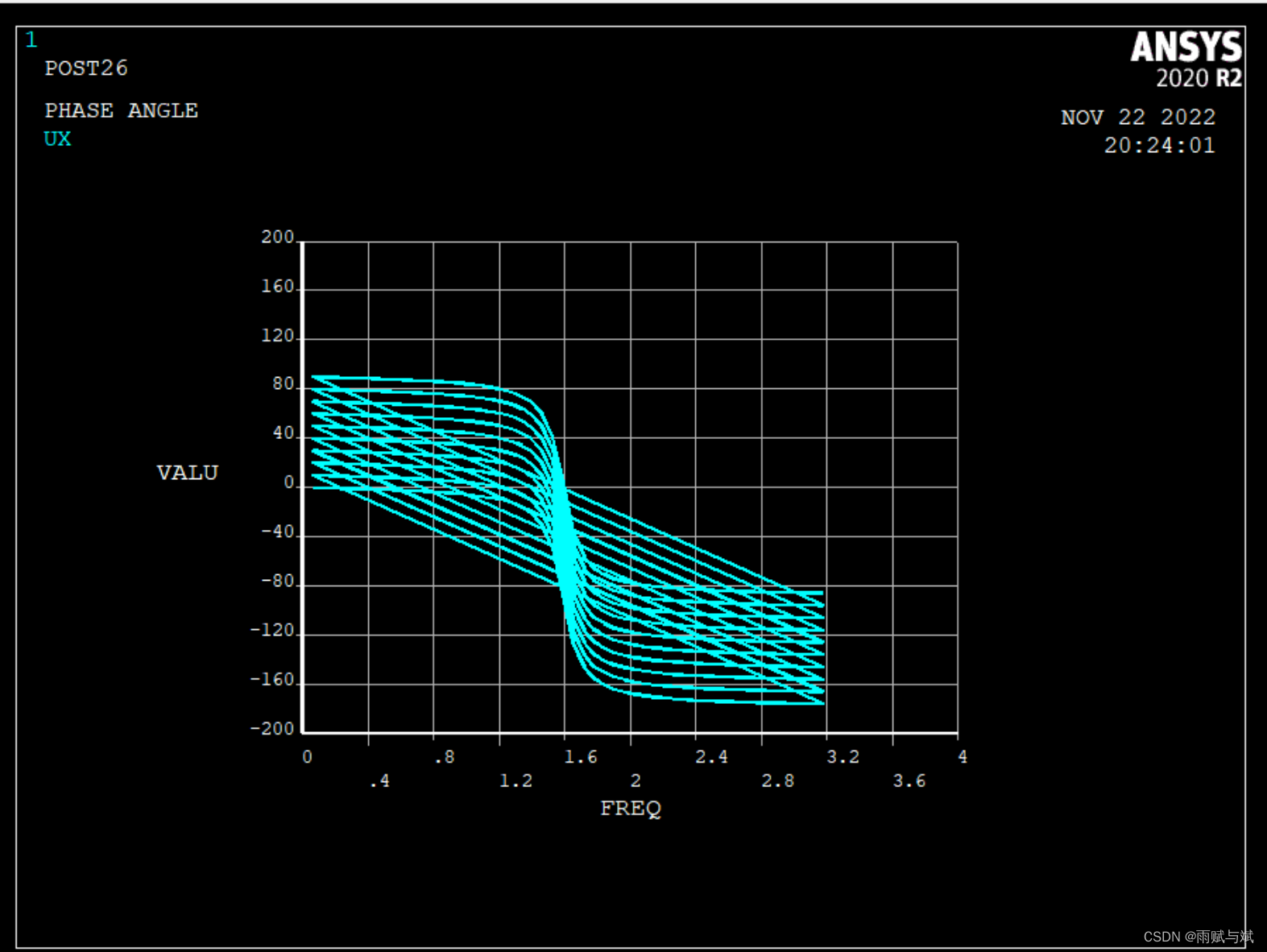
最后
以上就是时尚八宝粥最近收集整理的关于apdl多荷载步设置在第1荷载步50子步时,如图所示 在第2荷载步24子步时,如图所示 发现当图一中荷载为0时,图中没有弯矩,在第1的1和第2的25处最大值最小值相反,说明力的加载是按图1的线性变化加载的 当加入kbc=1,荷载阶跃后,荷载变化图如图 说明阶跃是从第一子步开始的的全部内容,更多相关apdl多荷载步设置在第1荷载步50子步时,如图所示 在第2荷载步24子步时,如图所示 发现当图一中荷载为0时,图中没有弯矩,在第1内容请搜索靠谱客的其他文章。








发表评论 取消回复