数据结构 - 用递归算法解决实际问题

实验题目：

编写一个程序exp5-2.cpp，求解背包问题：设有不同价值、不同重量的物品n件，求从这n件物品中选取一部分物品的方案，使选中物品的总重量不超过指定的限制重量，但选中物品的总价值最大。

源码：

#include<iostream>
#define Max 100
using namespace std;
struct bag
{
int weight;
int value;
};
int n;
int limweight;
int maxv;
int allvalue;
int setting[Max];
int cop[Max];
bag a[Max];
void find(int,int,int);
int main()
{
int k,w,v;
cout<<"物品种数：";
cin>>n;
for(allvalue=0,k=0; k<n; k++)
{
cout<<"第"<<k+1<<"种物品(重量，价值):";
cin>>w>>v;
a[k].weight=w;
a[k].value=v;
allvalue+=v;
}
cout<<"背包所能承受的总重量：";
cin>>limweight;
maxv=0;
for(k=0; k<n; k++)
cop[k]=0;
find(0,0,allvalue);
cout<<"最佳装填方案是："<<endl;
for(k=0; k<n; k++)
if(setting[k])
cout<<"
第"<<k+1<<"种物品"<<endl;
cout<<"总价值="<<maxv<<endl;;
}
void find(int i,int w,int v)
{
int k;
if(w+a[i].weight<=limweight)
{
cop[i]=1;
if(i<n-1)
find(i+1,w+a[i].weight,v);
else
{
for(k=0; k<n; k++)
setting[k]=cop[k];
maxv=v;
}
cop[i]=0;
}
if(v-a[i].value>maxv)
if(i<n-1)
find(i+1,w,v-a[i].value);
else
{
for(k=0; k<n; k++)
setting[k]=cop[k];
maxv=v-a[i].value;
}
}

基本思路：

第i件物品的选择有两种可能：

• 物品i被选择，这种可能性仅当包含它不会超过方案总重量的限制时才是可行的。选中后，继续递归去考虑其余物品的选择。
• 物品i不被选择，这种肯能性仅当不包含物品i也有可能会找到价值更大的方案的情况。

是否已拿完物品也就是i < n(i是当前物品序号，n是物品总数目)是否成立，如果成立则递归结束并打印输出路径。如果i < n则判断第i个物品能否放入背包，如果不能放入，则考虑放置i+1个物品，如果能放入还存在当前第i个放入和不放入两种情形后对第i+1个的影响。

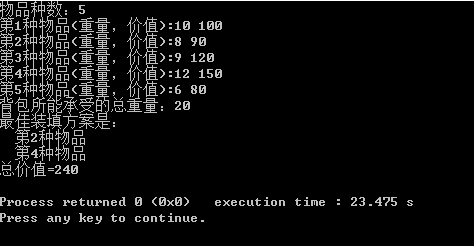
运行结果：

最后

以上就是激动黄蜂为你收集整理的数据结构 - 用递归算法解决实际问题的全部内容，希望文章能够帮你解决数据结构 - 用递归算法解决实际问题所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。