1、傅立叶(Fourier)变换及拉普拉斯(Laplace)变换
在MATLAB中,进行傅立叶变换的函数是:
fourier(f,x,t):求函数f(x)的傅立叶像函数F(t)。
ifourier(F,t,x):求傅立叶像函数F(t)的原函数f(x)。
在MATLAB中,进行拉普拉斯变换的函数是:
laplace(fx,x,t):求函数f(x)的拉普拉斯像函数F(t)。
ilaplace(Fw,t,x):求拉普拉斯像函数F(t)的原函数f(x)。
2、常用声音函数
lin2mu :将线性音频信号转换为mu法则
mu2lin :将mu法则转换为线性音频信号
sound :把向量转换为声音
soundsc :测量数据并作为声音播放
3、特殊声音函数
auread :读入next/sun声音文件(后缀为.au)
auwrite :写au声音文件
WAV声音文件
waveread :读声音文件
wavewrite:写声音文件
4、排序算法
colmmd :进行列的最小度排序
colperm :基于非零算法排序
dmperm :Dulmage-Mendelsohn分解
randperm:随机置换
symmmd :对称最小度排序
symrcm :反向Cuthill-McKee排序
condest :矩阵条件数估计
normest :矩阵范数估计
5、线性方程的稀疏系统
bicg :双共扼梯度法
bicgstab:双共扼梯度稳定法
cgs :二次共扼梯度法
cholinc :不完全Cholesky分解
cholupdate:Cholesky分解的秩1修正
gmres :广义最小残差法
luinc :不完全的LU分解
pcg :预处理共扼梯度法
qmr :Quasi_Minimal残差法
eigs :少数特征值和特征向量
svds :少数奇异值
spparms :设置稀疏矩阵程序的参数
6、inline函数
inline用来定义函数,使用方法如下:
【例一】
f = inline('x^2+1');
f(2)
ans =
5
【例二】
f = inline('x*y+9*x+7*y^2-2');
f(1,1)
ans =
15
定义匿名函数:
f=@(x)sin(x);%定义匿名函数f(x)=sin(x)
7、eval函数
eval函数可以用来计算“语句”串或者创建变量。
【例一】:创建变量
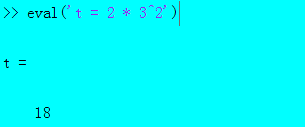
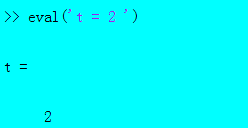 【例二】:计算“语句”串
【例二】:计算“语句”串


8、feval()函数
feval就是把已知的数据或符号带入到一个定义好的函数句柄中。下面举例说明:
【例一】:将数据带入定义好的函数句柄中
>> t = 2;
>> Y = inline('X^2 + Y^2');
>> k1 = feval(Y,1,t)
k1 =
5
>> k2 = feval(Y,t,0)
k2 =
4
>> k3 = feval(Y,1,2)
k3 =
5
>> k4 = feval(Y,1,1)
k4 =
2
>> k5 = Y(1,1)
k5 =
2
【例二】:将符号带入定义好的函数句柄中
>> syms t ;
>> H = inline('X^2 + Y^2');
>> k1 = feval(H,1,t)
k1 =
t^2 + 1
>> k2 = feval(H,t,1)
k2 =
t^2 + 1
>> k3 = feval(H,t^2,2*t)
k3 =
t^4 + 4*t^2
注:
- 对字符串类型函数只能用eval ,而不能用feval;
- 函数句柄只能被feval 运用,而不能被eval 调用.
9、测试向量中所有元素是否为真
all()函数可以测试向量中是否所有元素为真。
【例一】
>> A = 1:2:13
A =
1 3 5 7 9 11 13
>> all(A)
ans =
1
>> A = -3:1:3
A =
-3 -2 -1 0 1 2 3
>> all(A)
ans =
0
【例二】
>> B = [1 2 4;0 9 8;5 7 9]
B =
1 2 4
0 9 8
5 7 9
>> all(B)
ans =
0 1 1
>> C = [1 0 4; 2 5 -9; 90 8 12]
C =
1 0 4
2 5 -9
90 8 12
>> all(C)
ans =
1 0 1
10、计算向量的长度
10.1 lenth函数
>> A = [ 12 3 6 13];
>> length(A)
ans =
4
注:对于矩阵P而言,length(P)等价于max(size(P)).
10.2 numel函数
>>numel(A)
ans =
4
11、一些返回逻辑值的函数
| 函数 | 描述 |
| Iscell(C) | 若C是单元数组,则为真(即返回1) |
| Iscellstr(s) | 若s是字符单元数组,则为真 |
| Ischar(s) | 若s是字符串,则为真 |
| Isempty(A) | 若A是空数组[],则为真 |
| Isequal(A,B) | 若A和B有相同的元素和维数,则为真 |
| Isfield(S,’name’) | 若’name’是结构S的一个域,则为真 |
| Isfinite(A) | 若数组的元素有限,则为真 |
| Isinf(A) | 若数组的元素无限,则为真 |
| Isletter(A) | 若数组A的元素是字母表中的字符,则为真 |
| Islogical(A) | 若数组A是逻辑数组,则为真 |
| Ismember(A,B) | 若数组A的元素也是B的元素,则为真 |
| Isnan(A) | 若数组的元素为NaN,则为真 |
| Isnumeric(A) | 若A是数值数组,则为真 |
| Isprime(A) | 若A的元素是素数,则为真 |
| Isreal(A) | 若数组A的元素无虚部,则为真 |
| Isspace(A) | 若数组的元素为空白字符,则为真 |
| Issparse(A) | 若A是稀疏矩阵,则为真 |
| Isstruct(S) | 若S是一个结构,则为真 |
12、查找矩阵中满足条件的元素的下标
A = [1 2 3;4 5 6;7 8 9];
f = find(A);%找出A中非零元素的下标
f = find(A>2);%找出矩阵中元素值大于2的元素下标
f = find(3<A&A<6);%找出矩阵中元素值介于3,6的元素的下标
f = find(A~=2);%找出元素值不为2的元素的下标
13、获取变量类型
使用class(X)函数可以获取变量或者常量X的类型。
例:
>> A= [1+2*i 3;3 6];
>> class(A)
ans =
double
14、matlab中的日期时间函数
14.1说明
matlab中表示日期时间有三种格式:
(1)日期字符串(20-oct-2008等)
有很多格式可以选择,date函数返回的就是该格式
(2)连续日期数值(7.337417231638542e+005)
以公元元年1月1日为起点计算经过的天数,now函数返回的就是该格式
(3)日期向量(1.0e+003*[2.0070 0.0100 0.0280 0.0160 0.0210 0.0016])
[年 月 日 时 分 秒],clock返回的就是该函数
14.2获取当前日期时间函数
1.date:按照日期字符串格式返回当前系统日期
2.now:按照连续的日期数值格式返回当前系统时间
3.clock:按照日期向量格式返回当前系统时间
>>date,now,clock
ans =
29-Nov-2008
ans =
7.3374e+005
ans =
1.0e+003 *
2.0080 0.0110 0.0290 0.0160 0.0410 0.0259
14.3读取时间的某个部分
matlab中分别使用year,month,day,hour,minute,second从上面讲到的字符串和连续型日期时间格式中提取年月日时分秒等信息
>>[year(date),year(now)]
ans =
2008 2008
注意:上面的函数是没法从向量型日期时间格式中正确读取上述信息的
>>year(clock)
ans =
5 0 0 0 0 0
15、日期格式转换
1.datestr(D,F):将任意格式的日期时间D按指定格式F转成日期字符串格式
2.datenum:将任意格式的日期时间D转成连续日期格式
3.datevec:将任意格式的日期时间D转成时间向量格式
注意上面三种时间格式之间的任意转换有很多格式选择,根据需要自己调整,具体那些格式可以看帮助系统
16、计时函数
在编写程序时,经常需要获知代码的执行实际时间,这就需要在程序中用到计时函数,matlab中提供了以下三种方法:
1.cputime(单位不明)
返回matlab启动以来的CPU时间,可以在程序执行钱保存当时的CPU时间,然后在程序执行结束后用cputime减去运行前保存的数值,就可以获取程序的实际运行时间
>>t0=cputime;pause(3);TimeCost=cputime-t0
2.tic/toc(单位s)
tic用在程序的开始,作用是启动一个计时器,然后在程序尾部放一个toc,表示终止计时器,并返回tic启动以来的总时s间
3.etime(单位s)
etime(t1,t2)用来计算两个日期向量t1和t2之间的时间差,结合前面讲到的clock函数也可以用来确定程序代码的运行时间
>>t0=clock;pause(3);TimeCost=etime(clock,t0)
在三种计时中建议使用第二种,相对来说最精确。
17、求矩阵的条件数
cond(X,1);%求矩阵X的第一条件数
cond(X,2);%求矩阵X的第二条件数
cond(X,inf);%求矩阵X的无穷条件数
cond(X,’fro’);%求矩阵X的Frobenius条件数
cond(X);%求矩阵的第二条件数,等价于cond(X,2)
最后
以上就是传统导师最近收集整理的关于Matlab从入门到精通(五)--常用函数的全部内容,更多相关Matlab从入门到精通(五)--常用函数内容请搜索靠谱客的其他文章。








发表评论 取消回复