一、高斯法和Doolitle法
高斯法和Doolitle法都比较简单，其实Doolitle可以直接用maltab里面的lu命令来求，下面重点讲一下迭代法
二、Jacobi迭代
1.算法实现
Jacobi迭代的伪代码如下：
2.收敛条件
3.matlab实现
根据以上的算法可以写出一个简单的jacobi迭代如下：
复制代码
1
2
3
4
5
6
7
8
9function x = jacobi(a,b,k) n=length(b); d=diag(a); r=a-diag(d); x=zeros(n,1); for j = 1:k x = (b-r*x)./d; end
以上代码是最简单的写法，但是做题的时候一般要求把迭代过程给显示，这样写的话就不够完善，所以有以下拓展版
参数说明：
前两个变量为必选参量，分别问Ax=B的A和B，后三个参量为可选参量，分别为误差（默认为0.001），最大迭代次数（默认为1000），初始输入x矩阵（默认为零向量）p.s. 之后的Gauss迭代法和SOR法的参数都和Jacobi迭代法一样
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40function r = jacobi(A,B,varargin) sizeA=size(A); sizev=size(varargin); if sizev(2) == 0 rol = 0.000001; n = 1000; x = zeros(sizeA(1),1); elseif sizev(2) == 1 rol = varargin{1}; n = 1000; x = zeros(sizeA(1),1); elseif sizev(2) == 2 rol = varargin{1}; n = varargin{2}; x = zeros(sizeA(1),1000); elseif sizev(2) == 3 rol = varargin{1}; n = varargin{2}; x = varargin{3}; else error("输入参数过多"); end for i = 2:n for j = 1:sizeA(2) sum1=0; for k = 1:sizeA(1) if j == k continue; end sum1 = sum1 - x(k,i-1)*A(j,k)/A(j,j); end x(j,i)=B(j)/A(j,j)+sum1; end if any(abs(x(:,i)-x(:,i-1))>rol) == 0 break; end end r = x; end
4.结果展示
三、Gauss-Seidel迭代法
1.算法实现
Gauss-Seidel迭代法和Jacobi方法的位移差异是在前者中，最近更新的未知变量的值在每一步中都使用，即更新发生在当前步骤，举个例子方便例子。
构建的迭代公式如下：
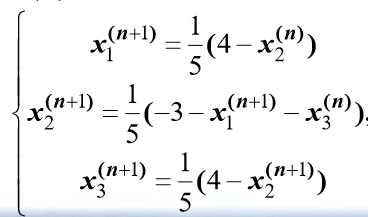
算法的伪代码如下：
2.matlab实现
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43function r = Gauss_Seidel(A,B,varargin) sizeA=size(A); sizev=size(varargin); if sizev(2) == 0 rol = 0.000001; n = 1000; x = zeros(sizeA(1),1); elseif sizev(2) == 1 rol = varargin{1}; n = 1000; x = zeros(sizeA(1),1); elseif sizev(2) == 2 rol = varargin{1}; n = varargin{2}; x = zeros(sizeA(1),1000); elseif sizev(2) == 3 rol = varargin{1}; n = varargin{2}; x = varargin{3}; else error("输入参数过多"); end for i = 2:n for j = 1:sizeA(2) sum1=0; for k = 1:j if j == k continue; end sum1 = sum1 - x(k,i)*A(j,k)/A(j,j); end for k = j+1:sizeA(1) sum1 = sum1 - x(k,i-1)*A(j,k)/A(j,j); end x(j,i)=B(j)/A(j,j)+sum1; end if any(abs(x(:,i)-x(:,i-1))>rol) == 0 break; end end r = x; end
3.结果展示
四、逐次超松弛(SOR)迭代法
1.算法实现
SOR方法使用Gauss-Seidel迭代法的求解方向，并使用过松弛以加快收敛速度，令w是一个实数，并将新的估计中的每个元素xk+1定义为w乘上Gauss-Seidel公式和1-w乘当前估计xk的平均，同样举个例子帮助理解：
迭代公式如下：
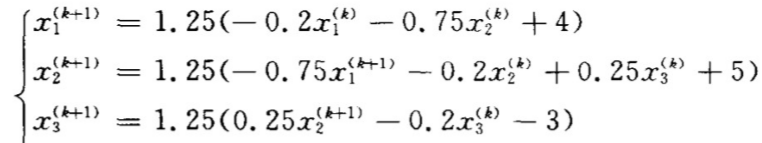
算法伪代码如下：
2.matlab实现
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44function r = SOR(A,B,w,varargin) sizeA=size(A); sizev=size(varargin); if sizev(2) == 0 rol = 0.000001; n = 1000; x = zeros(sizeA(1),1); elseif sizev(2) == 1 rol = varargin{1}; n = 1000; x = zeros(sizeA(1),1); elseif sizev(2) == 2 rol = varargin{1}; n = varargin{2}; x = zeros(sizeA(1),1000); elseif sizev(2) == 3 rol = varargin{1}; n = varargin{2}; x = varargin{3}; else error("输入参数过多"); end for i = 2:n for j = 1:sizeA(2) sum1=0; for k = 1:j if j == k sum1 = sum1 - w*(1-1/w)*x(k,i-1); continue; end sum1 = sum1 - w*x(k,i)*A(j,k)/A(j,j); end for k = j+1:sizeA(1) sum1 = sum1 - w*x(k,i-1)*A(j,k)/A(j,j); end x(j,i)=w*B(j)/A(j,j)+sum1; end if any(abs(x(:,i)-x(:,i-1))>rol) == 0 break; end end r = x; end
最后
以上就是腼腆柜子最近收集整理的关于MATLAB学数值分析（二） 迭代法解线性方程组的全部内容，更多相关MATLAB学数值分析（二）内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
发表评论 取消回复